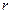|
|
Контрольные карты качественных признаковОценка качества продукции через изменение количественных параметров, например, длины изделия, не всегда целесообразна. В некоторых случаях наличие или отсутствие у изделия дефектов зависит от определенных качественных признаков. Например, керамическая фабрика производит китайскую керамику. По окончании процесса обжига каждое изделие подвергается проверке. Контролер выявляет изделия с дефектами лакового покрытия: трещинами, отколотыми кусачками и т.д. Если некоторое изделие имеет хотя бы один из этих признаков, оно относится к браку. В каждой партии продукции обязательно найдется несколько бракованных изделий. Конечно, ошибки всегда имеют место, но их появление должно быть редким и носить случайный характер. Вопрос, который должен задать себе производитель: соответствует ли доля бракованных изделий той доле, которая бывает при нормальных условиях, или имеются какие-то неполадки. Различают два типа контрольных карт качественных признаков. В р-картах используется удельный вес бракованных изделий, а в с-картах – число бракованных изделий, приходящихся на одну выборку. Остановимся более подробно на р-картах. Долю бракованных изделий в генеральной совокупности р в условиях контролируемого технологического процесса оценивают на основе большого числа выборок:
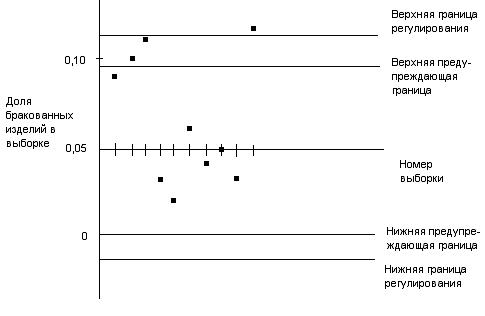
В р-картах долю бракованных изделий в выборке размера n принято обозначать через
Число бракованных изделий r в выборке размером в n изделий, полученной случайным образом из достаточно большой генеральной совокупности, имеет биномиальное распределение, если вероятность p того, что изделие окажется бракованным, является константой. При этом вероятность того, что в выборке размера n окажется r дефектных изделий, как было показано ранее, определяется зависимостью
Так как Стандартная ошибка распределения Поскольку расчет параметров биномиального распределения достаточно трудоемок, для упрощения расчетов его часто аппроксимируют либо распределением Пуассона, либо нормальным распределением. При этом обычно руководствуются такими правилами: В процессе аппроксимации используется распределение Пуассона, если При использовании любого из указанных распределений в процессе аппроксимации построение контрольной карты типа p аналогично построению описанной ранее контрольной карты среднего арифметического. При аппроксимации нормальным распределением процедура значительно упрощается и выглядит так: Центральная линия: она строится на уровне доли бракованных изделий в условиях контролируемого технологического процесса Предупреждающие границы: Границы регулирования: Построенную по этому алгоритму контрольную карту можно интерпретировать точно так же, как и контрольную карту среднего арифметического. Если для аппроксимации использовалось нормальное распределение, значения нижней предупреждающей границы и нижней границы регулирования могут оказаться отрицательными. Поскольку в данном случае отрицательные значения недопустимы, можно в этом случае либо не принимать во внимание нижние границы карты, либо провести аппроксимацию заново с использованием распределения Пуассона. Приведем пример. Компания производит микросхемы для компьютеров. В течение времени, когда было точно известно, что технологический процесс находится под контролем, было проведено 25 выборок по 100 микросхем в каждой. Оборудование было налажено соответствующим образом, использовалось сырье допустимого качества, наблюдение за ходом процесса осуществлял опытный оператор. Был проведен контроль качества изделий в каждой выборке. В таблице 1.2 приведены данные об обнаруженных бракованных изделиях. Таблица 1.2
Нужно построить контрольную карту качественного признака. Общее число бракованных изделий в 25 выборках равно 123, следовательно, оценка доли бракованных изделий в генеральной совокупности составит:
Хотя значение Центральная линия: 0,049. Предупреждающие границы: Границы регулирования: Так как Среднее число дефектов в выборке
Значения предупреждающих границ и границ регулирования, равные 0,001, 0,025, 0, 975 и 0,999, определяются в процессе расчета вероятностей, что показано в таблице. 1.3. Положим, что нижняя граница равна нулю, поскольку она не может иметь отрицательные значения. Положение оставшихся трех границ определяется как середина соответствующего интервала. Например, верхняя предупреждающая граница лежит между Таблица 1.3
Ниже приведены результаты аппроксимации двумя указанными распределениями(табл.1.4)
Таблица 1.4
На рисунке 1. 2 построена контрольная карта по результатам аппроксимации. Нижняя граница регулирования оказалась отрицательной, поэтому ее либо не наносят на карту, либо полагают равной нулю.
Рис.1.2 Та же компания продолжает осуществлять случайную выборку из готовых микросхем, объемом в 100 штук. Таблица 1.5 содержит информацию о числе бракованных изделий в 10-ти следующих друг за другом выборках. Используя эти данные, оценим, является ли технологический процесс контролируемым. Таблица 1.5
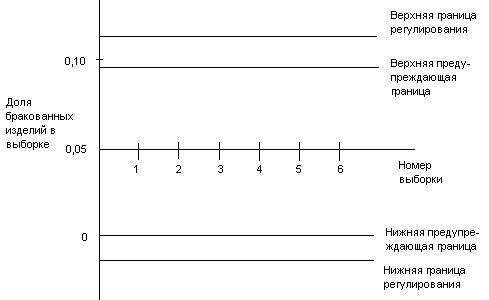
Нанесем выборочные доли на контрольную карту(рис. 1.3) Как видно в выборках №2 и №3 процесс вышел за верхнюю предупреждающую граница два раза подряд, следовательно он дожжен быть остановлен. Далее, видимо, после некоторых исправлений в технологическом процессе все выборки лежат в пределах предупреждающих границ. Но в момент выборки №10 процесс выходит из-под контроля и доля брака в этой выборке больше, чем верхняя граница регулирования, следовательно, процесс будет немедленно остановлен.
рис.1.3 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , где R – общее число бракованных изделий во всех выборках; N – общее число изделий, подвергшихся проверке.
, где R – общее число бракованных изделий во всех выборках; N – общее число изделий, подвергшихся проверке. . Эта величина определяется соотношением
. Эта величина определяется соотношением , где r – число бракованных изделий в выборке; n – число изделий в выборке.
, где r – число бракованных изделий в выборке; n – число изделий в выборке.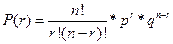 , r= 0, 1, 2, …, n.
, r= 0, 1, 2, …, n.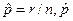 также имеет биномиальное распределение.
также имеет биномиальное распределение.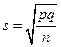
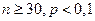 и
и  . Нормальное распределение используют как аппроксимирующее, если
. Нормальное распределение используют как аппроксимирующее, если 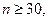
 ,
,  и
и 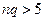 .
.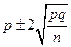 - в условиях контролируемого технологического процесса значение
- в условиях контролируемого технологического процесса значение  - в условиях контролируемого технологического процесса значение
- в условиях контролируемого технологического процесса значение 
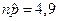 , то есть меньше 5, прибегнем к аппроксимации нормальным распределением и определим положение границ на контрольной карте.
, то есть меньше 5, прибегнем к аппроксимации нормальным распределением и определим положение границ на контрольной карте.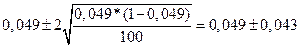 , то есть 0,006 и 0,092.
, то есть 0,006 и 0,092. , то есть -0,016 и 0,114.
, то есть -0,016 и 0,114.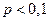 и
и 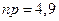 . Следовательно, распределение вероятностей Пуассона имеет вид:
. Следовательно, распределение вероятностей Пуассона имеет вид: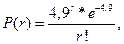
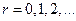
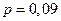 и
и 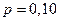 , и, следовательно, находится на уровне
, и, следовательно, находится на уровне 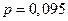 .
.