
|
|
И методические указания по контрольной работе12
 
1) уравнение этой прямой можно привести к уравнению с угловым коэффициентом: 2) Написать уравнение прямой, проходящей через точку Уравнение прямой через точку Условие параллельности Условие перпендикулярности 3) Уравнение прямой , проходящей через точку
4) Пример вычисления определителя разложением по строке или столбцу.
5) Решение системы уравнений по правилу Крамера.
Составим и вычислим основной определитель системы, составленный из коэффициентов при неизвестных. Будем его вычислять, используя разложение ,так как она содержит нулевой элемент и это упростит вычисления.
Основной определитель системы не равен 0 Для нахождения решения составим вспомогательные определения
Определители
6) Даны два вектора Задания к контрольной работе № 5 Контрольная работа содержит 5 заданий:
а) Построить эту линию по точкам от б) Найти уравнение этой линии в декартовой системе координат.
а) привести уравнение первой прямой к виду б) написать уравнение первой прямой в отрезках, в) написать уравнение второй прямой, проходящей через точку М и параллельной I прямой, г) написать уравнение третьей прямой, проходящей через точку М и перпендикулярной I прямой, д) написать уравнение четвертой прямой е) найти точку пересечения первой и четвертой прямых, ж) построить все четыре прямые.
а) скалярное произведение б) угол между векторами в) векторное произведение векторов
Контрольная работа № 6 Тема: «Неопределённые и определённые интегралы» Краткая теория и формулы:
Контрольная работа содержит три контрольных задания.
Контрольное задание № 1. Вычисление неопределённого интеграла I. Неопределенный интеграл есть
Основные правила интегрирования: 1. Дифференциал функции 2. 3. 4. Если 5. Если 6. Метод интегрирования по частям: если 7. Правильность результатов интегрирования проверяется так:
Таблица основных неопределённых интегралов
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. Формулы 1а, 2а, 3а, 5а, 6а, 10а, 11а получены по правилу 4. Для взятия неопределённого интеграла, надо преобразовать подынтегральное выражение, воспользоваться правилами, чтобы привести его к табличным интегралам. Контрольное задание № 2. Вычисление определённых и несобственных интегралов а) Определённый интеграл по формуле Ньютона-Лейбница
где б) Несобственный интеграл по бесконечному промежутку
Если предел существует, то несобственный интеграл сходится и равен ему, иначе интеграл расходится. Контрольное задание № 3. Приложение определённого интеграла для вычисления площади плоской фигуры. Площадь плоской фигуры, ограниченной сверху графиком функции

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 в декартовой системе координат,
в декартовой системе координат,  – в полярной системе координат.
– в полярной системе координат.



 :
:

 ;
; 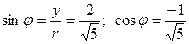
 ;
;  ;
;

 :
:

 ;
; 
 . Для того, чтобы построить график рекомендуется составить таблицу значений
. Для того, чтобы построить график рекомендуется составить таблицу значений  для угла
для угла  , значения через промежуток
, значения через промежуток  , отложить полученные точки
, отложить полученные точки  на плоскости и соединить их плавной линией (подробно построение графиков рассмотрено в методическом пособии стр. 5-6).
на плоскости и соединить их плавной линией (подробно построение графиков рассмотрено в методическом пособии стр. 5-6). .
. ,
,  – угол наклона прямой к оси ОХ.
– угол наклона прямой к оси ОХ. и а) параллельной данной прямой, б) перпендикулярной данной прямой.
и а) параллельной данной прямой, б) перпендикулярной данной прямой.
 ;
; ;
; ;
; и
и  .
. ;
;  ;
; 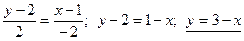 .
.



 , следовательно, система имеет единственное решение.
, следовательно, система имеет единственное решение. , которые получаются из основного определителя заменой в нем
, которые получаются из основного определителя заменой в нем  -го столбца столбцом свободных членов исходной системы.
-го столбца столбцом свободных членов исходной системы. (вычислим, используя разложение по первой строке)
(вычислим, используя разложение по первой строке) 
 и
и  вычислим используя разложения по первому столбцу.
вычислим используя разложения по первому столбцу.


 ,
,  . Найти площадь параллелограмма, построенного на этих векторах
. Найти площадь параллелограмма, построенного на этих векторах  .
.
 кв.ед.
кв.ед. в декартовой системе координат и точка
в декартовой системе координат и точка  в полярной системе координат. Построить эти точки. Определить полярные координаты точки
в полярной системе координат. Построить эти точки. Определить полярные координаты точки  и декартовы координаты точки
и декартовы координаты точки  .
. до
до  , придавая
, придавая  .
. и точки
и точки  и
и  .
. и определить угол наклона прямой к оси х,
и определить угол наклона прямой к оси х, , проходящей через точки
, проходящей через точки  и
и  ,
, ,
,  ,
,  и
и  . Найти:
. Найти: ,
, и
и  ,
, и
и  и площадь параллелограмма, построенного на них
и площадь параллелограмма, построенного на них 2)
2)  ; 3)
; 3)  4)
4) 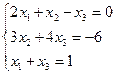 ; 5)
; 5) 
 2)
2)  ; 3)
; 3)  4)
4)  ; 5)
; 5) 
 2)
2)  ; 3)
; 3)  4)
4)  ; 5)
; 5) 
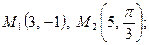 2)
2)  ; 3)
; 3)  4)
4)  ; 5)
; 5) 
 2)
2)  ; 3)
; 3)  4)
4)  ; 5)
; 5) 
 2)
2) 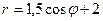 ; 3)
; 3)  4)
4)  ; 5)
; 5) 
 2)
2)  ; 3)
; 3)  4)
4)  ; 5)
; 5) 
 2)
2) 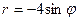 ; 3)
; 3)  4)
4)  ; 5)
; 5) 
 2)
2)  ; 3)
; 3)  4)
4)  ; 5)
; 5) 
 2)
2)  ; 3)
; 3)  4)
4)  ; 5)
; 5) 
 , где
, где  , С – постоянная
, С – постоянная  .
. называется первообразной для
называется первообразной для  .
. ;
;  .
. .
. (a – число).
(a – число). , то
, то 
 .
. , то
, то  .
. , то
, то  .
. . Взятие неопределённого интеграла есть действие, обратное взятию производной.
. Взятие неопределённого интеграла есть действие, обратное взятию производной. – постоянные числа;
– постоянные числа; , если
, если 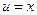 , то
, то  ;
;
 ;
;  ; 1а.
; 1а.  ;
; ; 2а.
; 2а.  ;
; ; 3а.
; 3а.  ;
; ;
; ; 5а.
; 5а.  ;
; ; 6а.
; 6а.  ;
; ;
; ;
;  ;
; ;
; ; 10а.
; 10а.  ;
; ; 11а.
; 11а.  .
. ;
; ,
, – первообразная функции
– первообразная функции  .
.
 , а снизу – графиком функции
, а снизу – графиком функции  при изменении х от а до b равна
при изменении х от а до b равна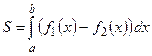 .
.