
|
|
Б. Обращение матрицы нормальных уравнений.Для вычисления матрицы N Обращение (8) удобно выполнять по схеме Жордана. Такую схему называют модифицированными жордановыми исключениями. Один шаг исключений выполняется в следующем порядке: 1. В матрице (8) выбирается разрешающий элемент а 2. Остальные элементы разрешающей строки R делятся на разрешающий элемент. 3. Остальные элементы разрешающего столбца S делятся на разрешающий элемент и меняют знаки. 4. Прочие элементы вычисляются по формуле:
(8)
(9) На втором шаге разрешающим будет второй преобразованный диагональный элемент матрицы (9), т.е. 47,751.
(10) На третьем шаге разрешающим берется третий диагональный элемент матрицы (10), т.е. 18,174.
(11) На последнем четвертом шаге разрешающим будет четвертый диагональный элемент 1,774 матрицы (11). Окончательный результат представляется в виде матрицы:
(12)
которая будет обратной к матрице (8). Контролем правильности обращения является равенство произведения матриц (8) и (12) единичной матрице с точностью 0,2. Кроме того при переходе с одного шага исключений к другому необходимо следить за симметричностью образовываемых матриц. Лишь в разрешающих строке и столбце соответственно слева и над разрешающим элементом, элементы матрицы различаются лишь знаками. Б.1 Преобразование матрицы в Excel. Как известно, названная обратная матрица вычисляется по формуле
где А – матрица уравнений поправок, Р - весовая матрица измерений. Следуя формуле необходимо задать матрицы А и Р, а потом выполнить над ними соответствующие преобразования.
В. Установление проектной точности угловых и линейных измерений. Средняя квадратическая ошибка взаимного положения пунктов опорной межевой сети не должна превышать 5 см. Это значит, что средняя квадратическая ошибка положения пункта полигонометрического хода в наиболее слабом месте не должна превышать 5 см. Согласно (1) и (12) можно записать, что: m m Теперь найдем: m m Наибольшей в данном случае будет средняя квадратическая ошибка положения первого пункта m1 Очевидно, что: m Или: m1= σ Но поскольку σ = 5/ Это значит, что в данном полигонометрическом ходе направления следует измерять с точностью до 4”,38. Но поскольку в полигонометрических ходах измеряют углы, а не направления, то: σβ = σ То есть точность измерения углов должна составлять 6”,2. Согласно инструкции в полигонометрии 4 класса, 1 и 2 разрядов точность измерений углов составляет 3”; 5”; 10”. В том случае, когда σ Таблица 3. Число приемов в полигонометрии.
Согласно табл. 3, теодолитом Т2 шестью приёмами обеспечивается точность 3”. Тогда одним приёмом будет обеспечена точность: σ1β = 3 Для достижения точности σ1β= 9,1” данным теодолитом необходимо выполнить приемов:
Округление здесь ведется до старшего целого числа. Теперь необходимо рассчитать точность измерения сторон. При составление матрицы нормальных уравнений, веса сторон приняты равными 0,5. Для расчета запишем известное из теории математической обработки геодезических измерений соотношение весов:
Где σ, р – соответственно стандарт и вес измерения направления, В данном случае Р=1, σ= 4”,4, Р Тогда:
Или:
Следовательно, в данном полигонометрическом ходе средняя квадратическая ошибка измерений угла не должна превышать 6”,2, а средняя квадратическая ошибка длин сторон - 6,2см.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 необходимо выполнить обращение матрицы нормальных уравнений.
необходимо выполнить обращение матрицы нормальных уравнений. и заменяется обратной величиной.
и заменяется обратной величиной.
 b
b  = a
= a  (7)
(7)
 На первом шаге жордановых исключений в качестве разрешающего применяется первый диагональный элемент 21,657. В результате исключений получается матрица:
На первом шаге жордановых исключений в качестве разрешающего применяется первый диагональный элемент 21,657. В результате исключений получается матрица:
 -1,309
-1,309





 = σ
= σ  *0,653 m
*0,653 m  = σ
= σ  = σ
= σ 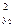 = σ
= σ  =
= 



 = σ
= σ 
 = 5 см, то:
= 5 см, то:
 = 6”,197
= 6”,197 
 не равно 3”, 5” или 10” необходимо рассчитать число приемов измерения углов исходя из следующей таблицы 3.
не равно 3”, 5” или 10” необходимо рассчитать число приемов измерения углов исходя из следующей таблицы 3. = 7”,3
= 7”,3 = 1,39= 2
= 1,39= 2
 - стандарт и вес измерения сторон.
- стандарт и вес измерения сторон. = 0,5.
= 0,5.
 ( см).
( см).