|
|
Скалярное произведение векторов в пространстве.
5) Вычислите косинус угла между векторами и выясните, какой угол (острый, прямой или тупой) образуют эти векторы, если
6) Вычислите угол между прямыми АВ и СD, если А(
Расстояние между двумя точками в пространстве 1) Ребро куба АВСDА1В1С1D1равно 2. Вычислите скалярное произведение векторов 2) Вычислите косинус угла между векторами и выясните, какой угол (острый, прямой или тупой) образуют эти векторы, если
3) Ребро куба АВСDА1В1С1D1равно р. Вычислите а) угол между прямыми А1В и АD1 б) расстояние между серединами отрезков АС1и В1С. 4) Вычислите угол между прямыми АВ и СD, если А(6;–4;8); В(8;–2;4); С(12;–6;4); D(14;–6;2) 5) Вычислите косинус угла между векторами и выясните, какой угол (острый, прямой или тупой) образуют эти векторы, если
6) Ребро куба АВСDА1В1С1D1равно р. Вычислите а) угол между прямыми АВ1и ВС1. б) расстояние между серединами отрезков АВ1и ВС1.
Уравнение плоскости. Уравнение сферы
Решение задач по теме « Координаты вектора»
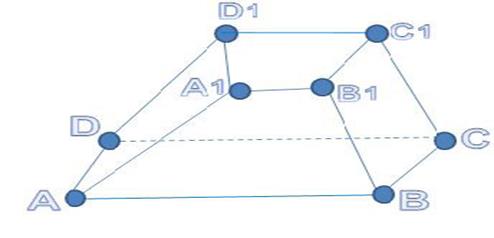
Тема 9. Многогранники Пространственные тела. 1)В прямоугольном параллелепипеде стороны основания равны 12 см и 2)В прямоугольном параллелепипеде АВСDА1В1C1D1 сторона основания АВ=4 м, боковое ребро АА1=6 м, А1С= 3) Для многогранника, изображенного на рисунке, выпишите элементы многогранника: вершины, грани, рёбра. Назовите диагонали боковых граней и диагонали многогранника.
4) Два тетраэдра имеют общую грань и расположены по разные стороны от нее. Данный многогранник является...
5) Поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело, называется ....
6) Составьте кроссворд по теме «Многогранники»
Параллелепипед 1) Стороны основания прямого параллелепипеда 8 и 15 и образуют угол 60°. Меньшая из площадей диагональных сечений равна 130. Найти площадь поверхности. 2) Диагональ прямоугольного параллелепипеда равна 25, диагональ одной из граней – 24. Найти длину ребра, перпендикулярного к данной грани. 3) Диагональ одной из граней прямоугольного параллелепипеда равна 15, а ребро перпендикулярное этой грани имеет длину 8. Найти диагональ параллелепипеда. 4) Диагональ прямоугольного параллелепипеда 11, измерения параллелепипеда относятся как 6:6:7. Найти диагональ параллелепипеда. 5) В прямоугольном параллелепипеде стороны 5 и 12. Диагональ параллелепипеда образует угол 45°с плоскостью основания. Найти боковое ребро и площадь диагонального сечения. 6) В прямоугольном параллелепипеде стороны основания 15 и 8, площадь диагонального сечения 340. Найти боковое ребро.
Призма. 1) Сторона основания правильной четырехугольной призмы АВСDА1В1С1D1равна 4см, а боковое ребро равно 7 см. Найти площадь сечения, которое проходит через ребро АА1и вершину С. 2).В основании прямой призмы АВСА1В1С1лежит прямоугольный треугольник АСВ (угол С = 90°), АС = 4см, ВС = 3см, угол В1АС = 60°. Найти площадь боковой поверхности призмы. 3). Основание прямой призмы – треугольник со сторонами 6 см и 8 см и углом, равным 900, между ними. Наибольшая из площадей боковых граней равна 40 см2. Найдите площадь боковой поверхности призмы. 4). В основании прямого параллелепипеда АВСDА1В1С1D1 лежит ромб АВСD со стороной, равной а и углом ВАD, равным 60°. Плоскость ВС1D составляет с плоскостью основания угол 60°. Найти площадь полной поверхности параллелепипеда. 5)Сторона основания правильной треугольной призмы равна 6 см, а диагональ боковой грани 10 см. Найдите площадь боковой и полной поверхности призмы. 6)Основание прямой призмы - равнобедренный треугольник с боковой стороной 6 см и углом при вершине 1200. Диагональ наибольшей боковой грани образует с плоскостью основания призмы угол 600. Найдите площадь боковой и полной поверхности призмы.
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
.
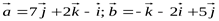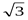;1;0);В(0;0; 
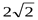); С(0;2;0); D( 
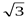;1;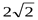 
)
.
.
.
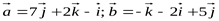6) Ребро куба АВСDА1В1С1D1равно 2. Вычислите скалярное произведение векторов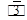 
см. Диагональ параллелепипеда образует с плоскостью основания угол в 300. Найдите эту диагональ параллелепипеда.
м. Найдите AD.