
|
|
Перестановки без фиксированных парПостановка задачи: Обозначим через
Решение: Для вычисления Перестановки, обладающие свойством Перестановки, обладающие двумя свойствами, т.е. имеющие две упорядоченные пары, например Если к=i+1 , то перестановки составляем из (i, i+1, i+2) и (n-3) остальных элементов, т.е. тоже из (n-2) элементов.
Всего пар может быть - (n-1), следовательно:
Распределение объектов по ячейкам
Даны - объекты могут быть одинаковыми или различными; - ячейки могут быть одинаковыми или различными; - возможно ограничение на количество объектов в ячейках; - возможен учёт порядка объектов в ячейках или порядка ячеек. Прежде чем рассмотреть решения различных вариантов постановки задачи распределения объектов по ячейкам, введём условные обозначения: 0 0 0 …0 – объекты (m штук); / – перегородка, отделяющая одну ячейку от другой (всего перегородок k-1 штук). Приведём несколько примеров распределения объектов по ячейкам с учётом введённых обозначений:
Перейдём к обзору методов решения основных задач распределения объектов по ячейкам.
Распределение одинаковых объектов Во всех следующих задачах (кроме пункта 5.4) предполагается, что ячейки различны и различают их по номерам: Вместимость ячеек неограниченна, ячейки не могут быть пустыми
Ввиду условных обозначений, данная задача может быть переформулирована следующим образом: необходимо в
Вместимость ячеек неограниченна, ячейки могут быть пустыми
При данной формулировке задачи перегородки (т.е./) могут стоять произвольным образом, т.е. возможны следующие варианты:
/ / 0 0 / 0…0 – два объекта в третьей ячейке, все остальные – в последней; ……………. /…/ 0…0 – все объекты в последней ячейке. Следовательно, из имеющихся
Получаем – сочетания с повторениями. Возможен другой способ рассуждений. Любому объекту ставится в соответствие номер ячейки, в которую он попал. Таких номеров
Вместимость каждой ячейки не менее, чем l объектов
Сначала в каждую ячейку помещаем по l объектов, а затем оставшиеся (m-k*l) объектов распределяем без ограничения на число объектов в ячейке (как описано в случае 1.2). Получаем количество способов распределения:
Распределение различных объектов по ячейкам без учёта порядка объектов в ячейке Вместимость ячеек неограниченна, ячейки могут быть пустыми Любой объект может попасть в любую ячейку. Т.е. первый объект можно поместить в любую из k ячеек, второй (независимо от первого) также поместить в любую из k ячеек и т.д. По правилу произведения результат будет следующим:
Вместимость ячеек задана Пусть вместимость первой ячейки – n1, вместимость второй ячейки – n2, …вместимость k-ой ячейки – nk. Причём По правилу произведения число способов заполнения всех ячеек равно:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 - число таких перестановок
- число таких перестановок  чисел
чисел  , что ни одна из этих перестановок не содержит ни одной из упорядоченных пар
, что ни одна из этих перестановок не содержит ни одной из упорядоченных пар  .
. , если она содержит i–тую упорядоченную пару (i, i+1). Число всех перестановок
, если она содержит i–тую упорядоченную пару (i, i+1). Число всех перестановок  .
. и пары
и пары  , рассматриваемой как один элемент. Следовательно, независимо от
, рассматриваемой как один элемент. Следовательно, независимо от  .
. , получаются из пар
, получаются из пар  , каждая из которых рассматривается как отдельный элемент и
, каждая из которых рассматривается как отдельный элемент и  оставшихся элементов, т.е. из (n-2) элементов.
оставшихся элементов, т.е. из (n-2) элементов. независимо от
независимо от  . Число перестановок, не обладающих ни одним из свойствами
. Число перестановок, не обладающих ни одним из свойствами  , зависит только от
, зависит только от 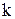 и
и  .
.
 объектов (предметов) и
объектов (предметов) и  - все объекты попали в последнюю ячейку;
- все объекты попали в последнюю ячейку; - три объекта в первой ячейке, все остальные в последней.
- три объекта в первой ячейке, все остальные в последней. .
. интервале между объектами разместить
интервале между объектами разместить  перегородку так, чтобы две перегородки не стояли рядом. Это можно сделать
перегородку так, чтобы две перегородки не стояли рядом. Это можно сделать  способами (до первой перегородки – в первую ячейку, между первой и второй – во вторую, и т.д.).
способами (до первой перегородки – в первую ячейку, между первой и второй – во вторую, и т.д.). мест необходимо выбрать места для
мест необходимо выбрать места для перегородки. Количество способов, которыми это можно сделать равно
перегородки. Количество способов, которыми это можно сделать равно
 .
.
 . Объект для первой ячейки может быть выбран
. Объект для первой ячейки может быть выбран  способами, для второй –
способами, для второй –  и т.д.
и т.д. .
.