
|
|
Размещения из n элементов по mМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ ГОСУДАРСТВЕННОЕ ВЫСШЕЕ УЧЕБНОЕ ЗАВЕДЕНИЕ «ДОНЕЦКИЙ НАЦИОНАЛЬНІЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Методические указания и варианты к индивидуальному заданию по курсу «ОДМ, часть 1» для студентов, обучающихся по направлению подготовки «Компьютерные науки»
Донецк-2010 Тема1 Основные понятия комбинаторики: соединения без повторений
Правила суммы и произведения Важную роль при решении многих комбинаторных задач играют правила суммы и произведения. Сформулируем эти правила с точки зрения теории множеств и комбинаторики. Правило суммы Теоретико-множественная формулировка правила суммы Пусть A и B – конечные множества, | A | = m; | B | = n; A Ç B = Æ. Тогда объединение множеств: A È B содержит m + n элементов.
В общем случае. Пусть | M1 | = m1, | M2 | = m2 , … , | Mk | = mk и Mi Ç M j = Æ, " i,j=1.. k, i ¹ j. Тогда, | M | = | M1 È M2 È … È Mk | = m1 + m2 +…+ mk. Комбинаторная формулировка правила суммы Если объект a может быть выбран m способами, а объект b – n другими способами, то выбор "a или b" может быть осуществлен m + n способами. Выбор a и b – взаимоисключающий: выбор a исключает выбор b; выбор a не совпадает с каким-либо способом выбора b.
В общем случае. Если объект a1 может быть выбран m1 способами; a2 – m2 cпособами; … ; ak – mk способами. Выбор "a1 или a2…или ak " может быть осуществлен m1 + m2 + … + m k способами. Например: Из Киева в Донецк в течение суток отправляется 3 поезда, 1 самолет и 2 автобуса. Сколько существует способов выехать из Киева в Донецк? Решение: По правилу суммы имеем N= 3+1+2 = 6 способов.
Правило произведения Теоретико – множественная формулировка правила произведения
Если A и B – конечные множества и | A | = m, | B | = n, то мощность множества A´B равна m´n.
В общем случае. Если | M1 | = m1, | M2 | = m2, … , | Mk |=mk, то | M1 ´ M2 ´ … ´ Mk | = m1´m2´…´mk.
Комбинаторная формулировка правила произведения
Если объект a может быть выбран m способами, и после этого объект b может быть выбран n способами, то выбор пары (a, b) может осуществляться m´n способами (выбор a и b независимы). В общем случае. Пусть объект a1 может быть выбран m1 способом, объект a2 – m2 способами; объект ak – mk способами, причем выбор a1 не влияет на число способов выбора a2, … ,ak, выбор a2 на число способов выбора a3, … ,ak и т.д. Тогда, выбор упорядоченного множества объектов (a1, a2 …ak) – в указанном порядке можно осуществить m1´ m2´… ´mk способами. Например: Сколько различных танцующих пар можно составить из 3-х девушек и 2-х юношей?
Решение: Число способов выбрать одну девушку из трех равно 3, при каждом способе выбора девушки число способов выбрать юношу постоянно и равно 2.По правилу произведения имеем N = 3´2 = 6 пар.
Сложный выбор объектов
Часто в комбинаторных задачах выбор объектов происходит в несколько ступеней, на некоторых работает правило суммы, на других – правило произведения. При сложном выборе объектов важно обеспечить полный перебор всех возможных случаев.
Например: Имеется три различных флага. На флагштоке поднимается сигнал, состоящий не менее, чем из 2-х флагов. Сколько различных сигналов можно поднять на флагштоке, если порядок сигналов учитывается? Решение: Сигнал может состоять либо из 2-х флагов, либо из 3-х. Одновременное выполнение 2-х действий невозможно. Пусть N – общее число способов поднять сигнал, состоящий не менее, чем из 2 флагов; N2 – число способов поднять сигнал, состоящий ровно из 2 флагов; N3 – ровно из 3 флагов. По правилу суммы имеем: N = N2 + N3 . Далее N2 и N3 находим по правилу произведения: N2=3´2=6; N3=3´2´1=6. В итоге имеем: N=12.
Соединения без повторений
Соединения – простые комбинаторные объекты, к которым относятся перестановки, сочетания и размещения.
Перестановки Перестановка из n элементов – упорядоченная последовательность элементов n-элементного множества (кортеж). Различные перестановки отличаются только порядком элементов в них.
Определим 0!=1
Пусть A = {1,2,3}.Число различных перестановок равно 3!=6.
Сгенерируем все перестановки во множестве A: {123, 132, 213, 231, 312, 321}.
Например: 1) Число способов стать в очередь за стипендией из 17 человек? P17=17! 2) Сколькими способами можно расставить на полке 5 книг? P5=5! 3) Сколько различных слов можно образовать, переставляя буквы в слове “ковш”? P4=4!
Размещения из n элементов по m
Размещения – упорядоченная последовательность из m элементов множества, содержащего всего n элементов. Различные размещения отличаются составом элементов и (или) порядком их следования.
Пусть A={1,2,3}. Сгенерируем всевозможные размещения из 3 по 2: {12, 21, 13, 31, 23, 32}.
1) Сколькими способами можно расставить на полке 5 книг из 7? Решение: Поскольку порядок книг на полке имеет значение, то число способов равно 1) Сколько различных четырёхсимвольных идентификаторов можно получить в алфавите {A,B,C,D,E}. Решение: С учетом того, что порядок символов в идентификаторе имеет значение, получим Замечание: Формула При m = n
Сочетания
Сочетания из n по m – последовательность из m элементов, взятых из n-элементного множества, без учета порядка следования элементов. Сочетание– произвольное (неупорядоченное) m-подмножество из n элементов.
1)
2)
3) Симметричность числа сочетаний:
4) Правило Паскаля. Для числа сочетаний из n по m справедливо следующее рекуррентное соотношение:
5) Бином Ньютона.
При a = x = 1,
Пусть A={1,2,3}. Сгенерируем всевозможные сочетания из 3 по 2: {12, 31, 32}.
Например: 1) Сколькими способами можно выбрать 4 человека из 52 в президиум собрания? Решение: Поскольку порядок выбора не имеет значения, получим:
2) Определить число способов, которыми можно выбрать 5 карт из 36 так, чтобы среди них были 3 карты одного достоинства? Решение: В колоде из 36 карт четыре масти и в каждой 9 достоинств (короли, тузы…). Число способов выбрать одно достоинство равно 9 или
Тогда, число способов выбрать 3 карты одного достоинства равно 9* Оставшиеся две карты могут быть любыми из 33 карт, то есть
Основные понятия комбинаторики: соединения с повторениями
До сих пор рассматривали соединения из множеств, состоящих из различных элементов. Часто на практике имеют место случаи, когда среди рассматриваемых элементов есть одинаковые.
Пусть дано множество А, состоящее из n элементов, в котором n1 элементов принадлежит первому типу; n2 элементов принадлежит второму типу элементов, nk - k-тому типу. Элементы одного и того же типа неразличимы между собой.
Спецификацией множества А называется набор (n1, n2, … ,nk).
Следствие: Если множество А, | А | = n, состоит из объектов 2 типов: m-одного типа, (n – m) –другого:
В общем случае:
Например: Сколько различных чисел можно получить, переставляя цифры числа 12341234? Решение: В числе 8 цифр: две-“1”; две-“2”; две-“3”; две-“4”. Например: Сколько различных перестановок можно образовать из всех букв слова “Миссисипи”? Решение: Всего в слове 9 букв, из них – 4 буквы “и”, три буквы ”с”, одна буква ”м” и одна буква ”п”.
Размещения с повторениями (m перестановки с неограниченными повторениями)
Пусть А = {a1, a2,…, an} , где a1, a2,…, an – “представители” 1-го, 2-го, … n-го типа элементов. Объектов каждого типа имеется в неограниченном количестве, элементы одного типа неразличимы между собой. Рассмотрим следующую схему выбора упорядоченной последовательности из m элементов: выбираем элемент на 1-е место, имеется n вариантов выбора. После этого элемент возвращается обратно и может быть выбран еще, т.е. на 2-е место имеется n претендентов и т.д. На m-е место также имеется n претендентов.
Например: Сколько различных сигналов могут дать 4 светофора одновременно?
Решение: Число различных сигналов на одном светофоре равно 3. Разные светофоры могут подавать одинаковые сигналы. Тогда, N- число различных сигналов, равно числу различных размещений с повторениями из 3 по 4:
Сочетания с повторениями
Пусть А = {a1, a2,…, an}, где a1, a2,…, an - “представители” 1-го, 2-го, …, n-го типа элементов. Объектов каждого типа имеется в неограниченном количестве, элементы одного типа неразличимы между собой. Сочетания с повторениями отличаются составом элементов, входящих в выбираемое множество. Порядок элементов не имеет значения. Имеет значение, сколько элементов каждого типа вошло в сочетание. Рассмотрим определенное сочетание. Пусть в него входят: r1 объектов 1-го типа, r2 объектов 2-го типа, . . . . . . . . . . rn объектов n-го типа;
Некоторые ri могут быть равны 0. Сочетанию можно поставить в соответствие следующую схему:
Вертикальные черточки отделяют элементы одного типа от элементов другого. Если элементов какого-либо типа нет, две черты будут рядом. Количество черточек равно (n-1). Каждому сочетанию с повторениями соответсвует схема и наоборот, каждая подобная схема соответствует некоторому сочетанию с повторениями.
Количество сочетаний с повторениями из n по m равно числу таких схем.
Всего в схеме (n – 1) + m объектов, (n – 1) – черточек и m – нулей. Число схем равно числу различных перестановок из (n + m – 1) – элементов, среди которых (n – 1) – одинаковых “ | ” и m – одинаковых “0”.
Например: 1) В кондитерской продают 4 вида пирожных. Сколькими
способами один человек может купить 8 пирожных?
2) В кондитерской продают 4 вида пирожных. Сколькими способами 8 различных человек могут купить по 1 пирожному?
Формулы пересчета для основных видов комбинаторных соединений

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 Например:
Например: .
. .
. верна для всех m £ n.
верна для всех m £ n. .
. Различные сочетания отличаются составом элементов, но не их порядком.
Различные сочетания отличаются составом элементов, но не их порядком. Þ
Þ  ;
; ;
;  ;
; 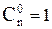 ;
;  при m £ 0 и m ³n .
при m £ 0 и m ³n . .
. .
.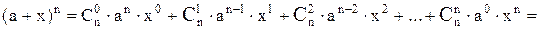
 .
. ,
,  ,где
,где , k = 0,1… n - биномиальные коэффициенты.
, k = 0,1… n - биномиальные коэффициенты. .
. .
.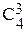
 . По правилу произведения имеем:
. По правилу произведения имеем: 
 .
. .
. .
. .
.
 .
. .
.










