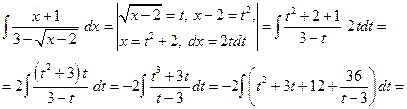|
|
Интегрирование неправильных дробейВсякую неправильную дробь путем деления числителя на знаменатель можно представить в виде суммы некоторого многочлена и правильной дроби:
где Пример 20.Найти интеграл Подынтегральная дробь является неправильной, поскольку степень числителя больше степени знаменателя. Для того, чтобы ее проинтегрировать, необходимо сначала выделить целую часть, т.е. представить дробь в виде суммы многочлена и правильной дроби:
После этого интеграл может быть представлен в виде суммы простых интегралов:
ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 8.1. Интегралы вида (R – рациональная функция) Неопределенный интеграл вида Сделаем подстановку
Выразим
Тогда где Пример 21.Найти интеграл Воспользуемся универсальной тригонометрической подстановкой (16), которая позволит перейти к интегралу от дробно-рациональной функции.
Несмотря на то, что универсальная подстановка дает возможность проинтегрировать всякую функцию вида 1. Если подынтегральная функция четная относительно
После подстановки получается интеграл от рациональной функции. Пример 22.Найти интеграл Подынтегральная функция четна относительно sin x и Итак,
Тогда получаем:
2. Если подынтегральная функция нечетная относительно 3. Если подынтегральная функция нечетная относительно Пример 23. а)Найти интеграл Подынтегральная функция нечетная относительно
б) Найти интеграл Подынтегральная функция нечетная относительно
8.2. Интегралы вида 1.По крайней мере один из показателей степени, m или n – нечетное положительное число. Если n – нечетное положительное число, то применяют подстановку 2. Если оба показателя степени, m и n – четные положительные числа, то для преобразования подынтегральной функции используют формулы понижения степени:
Пример 24. а)Найти интеграл
б)Найти интеграл Показатели степени у
Найдем два последних интеграла.
Окончательно получаем:
8.3. Интегралы вида С помощью тригонометрических формул:
интегралы такого вида можно представить в виде суммы (разности) простых интегралов. Пример 25.Найти интеграл Преобразуем подынтегральное выражение, пользуясь формулой (20):
Тогда можно представить исходный интеграл как разность двух интегралов:
Интегрирование некоторых иррациональных выражений Интегрирование выражений вида
Интеграл вида Пример 26.Найти интеграл Это интеграл вида
9.2. Интегралы от выражений вида Интеграл вида Пример 27.Найти интеграл
Пример 28.Найти интеграл С помощью замены переменной перейдем к интегралу от дробно-рациональной функции.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
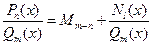 , (15)
, (15)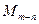 и
и 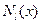 – многочлены,
– многочлены, 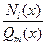 – правильная дробь,
– правильная дробь, 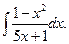
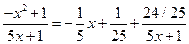 .
.
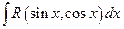
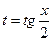
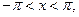 которая называется универсальной тригонометрической подстановкой, сводится к неопределенному интегралу от рациональной функции одной переменной
которая называется универсальной тригонометрической подстановкой, сводится к неопределенному интегралу от рациональной функции одной переменной 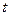 .
.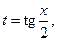
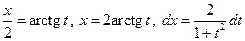 . (16)
. (16)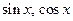 через
через 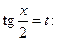

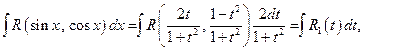
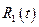 – рациональная функция от
– рациональная функция от 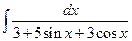 .
.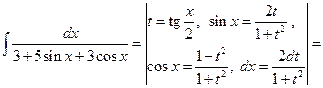


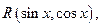 однако на практике она часто приводит к слишком сложным рациональным функциям. Поэтому наряду с универсальной подстановкой полезно знать и другие подстановки, которые в некоторых случаях быстрее приводят к цели.
однако на практике она часто приводит к слишком сложным рациональным функциям. Поэтому наряду с универсальной подстановкой полезно знать и другие подстановки, которые в некоторых случаях быстрее приводят к цели.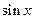 и
и 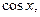 то есть
то есть 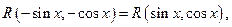 то применяется подстановка
то применяется подстановка 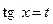 , так как
, так как 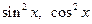 выражаются рационально через
выражаются рационально через 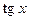 :
: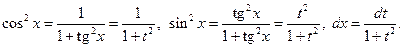
 .
.
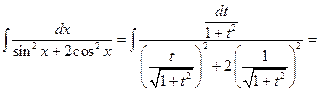
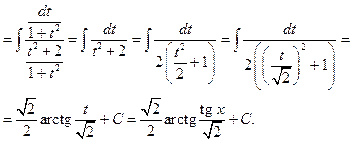
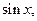 то есть
то есть 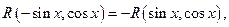 то он приводится к интегралу от рациональной функции заменой:
то он приводится к интегралу от рациональной функции заменой: 
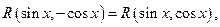 то он приводится к интегралу от рациональной функции заменой
то он приводится к интегралу от рациональной функции заменой 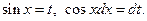
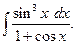
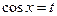 .
.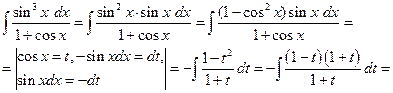
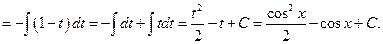
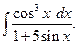
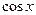 , поэтому сделаем подстановку
, поэтому сделаем подстановку  .
.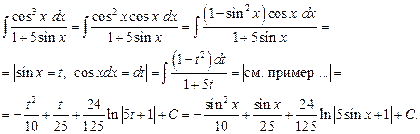
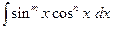
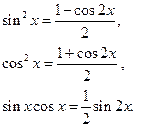 (17)
(17)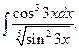
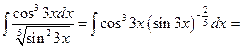
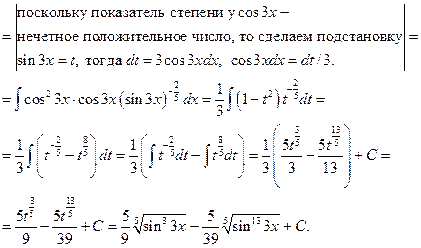
 .
. и
и 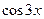 - целые положительные числа, поэтому преобразуем подынтегральную функцию с помощью формул (17):
- целые положительные числа, поэтому преобразуем подынтегральную функцию с помощью формул (17):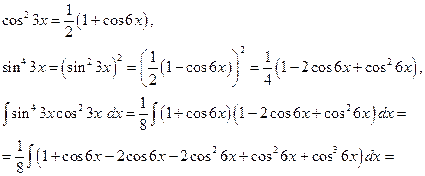
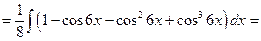
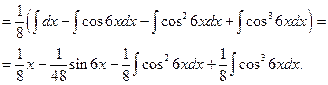
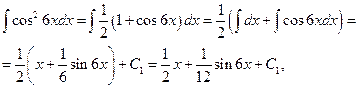
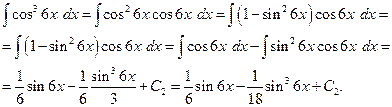
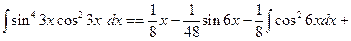
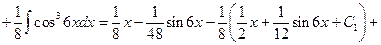
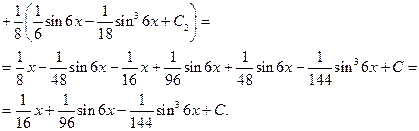

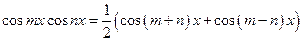 , (18)
, (18)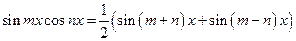 , (19)
, (19)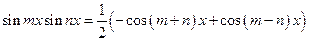 (20)
(20)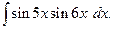
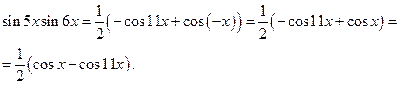

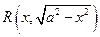 ,
, 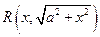 ,
, 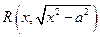
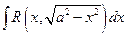 может быть приведен к интегралу от рациональной функции с помощью замены
может быть приведен к интегралу от рациональной функции с помощью замены  или
или 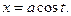 Для интеграла вида
Для интеграла вида 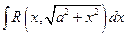 с этой целью используют замены
с этой целью используют замены 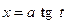 или
или 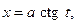 а для интеграла вида
а для интеграла вида 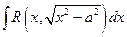 - замены
- замены 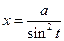 или
или  .
.
 (точно также можно воспользоваться и подстановкой
(точно также можно воспользоваться и подстановкой 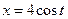 ).
).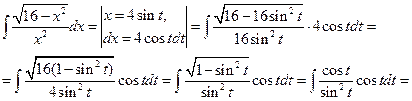
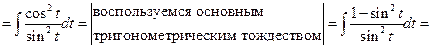

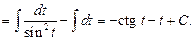
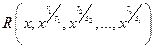
 приводится к интегралу от рациональной функции с помощью замены
приводится к интегралу от рациональной функции с помощью замены 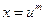 , где m = НОК (
, где m = НОК (  .
.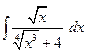 .
.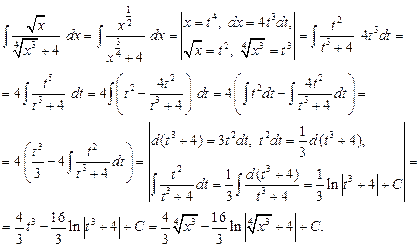
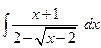 .
.