
|
|
Подведение под дифференциалИНДИВИДУАЛЬНЫЕ ДОМАШНИЕ ЗАДАНИЯ К РАЗДЕЛУ «ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ для индивидуальной самостоятельной работы по разделу «Интегральное исчисление» курса «Математика» для студентов профилей 12.03.04 «Биотехнические и медицинские аппараты и системы», «Менеджмент и управление качеством в здравоохранении» очной формы обучения
Воронеж 2015 Понятие первообразной функции Функция F(x) называется первообразной для функции f(x) на некотором промежутке изменения переменной Понятие неопределенного интеграла Неопределенным интегралом от функции f(x) называется множество всех первообразных для этой функции. Обозначение: ∫ f(x)dx = F(x) +C, где F(x) – некоторая первообразная для f(x), C – произвольная постоянная, Свойства неопределенного интеграла 1. Производная от неопределенного интеграла по переменной интегрирования равна подынтегральной функции:
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:
3. Неопределенный интеграл от производной от некоторой функции равен сумме этой функции и произвольной постоянной:
4. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
5. Неопределенный интеграл от суммы функций равен сумме неопределенных интегралов от слагаемых:
6. Постоянный множитель можно выносить за знак неопределенного интеграла:
Таблица основных неопределенных интегралов
Пример 1.Найти интеграл Преобразуем подынтегральное выражение, а затем воспользуемся свойством 5 и первым табличным интегралом.
5. Замена переменной Введение новой переменной помогает привести заданный интеграл к табличному или сводящемуся к табличному. Общих методов подбора новой переменной не существует. Однако в некоторых случаях могут быть даны следующие рекомендации. Линейная замена Интегралы вида
Итак,
где F – первообразная функции f. Пример 2.Найти интеграл Согласно свойству 5, этот интеграл может быть представлен в виде суммы интегралов:
Найдем первый интеграл, упростив его с помощью линейной замены.
Очевидно, что проще было бы избежать введения новой переменной, а воспользоваться формулой (7) и сразу записать: Пользуясь формулой (7), найдем остальные интегралы:
Окончательно запишем:
Пример 3.Найти интеграл Преобразуем подынтегральное выражение и с помощью замены переменной сведем этот интеграл к табличному.
Подведение под дифференциал Если в подынтегральном выражении уже есть дифференциал функции Заметим, что в этом случае можно не вводить новую переменную t, а записать интеграл в виде:
Формулу (8) называют также формулой подведения под дифференциал. Пример 4.Найти интеграл
Пример 5.Найти интеграл
Пример 6.Найти интеграл
Пример 7.Найти интеграл
Пример 8.Найти интеграл
Пример 9.Найти интеграл
6. Интегрирование по частям Метод интегрирования по частям основан на формуле
Применение этой формулы целесообразно тогда, когда интеграл в правой части формулы проще, чем исходный интеграл. В некоторых случаях необходимо применять формулу несколько раз. В частности, этим методом пользуются для нахождения интегралов вида
и где Также с помощью интегрирования по частям находятся интегралы вида
В общем случае за u обозначается та функция, которая упрощается при дифференцировании, а за v – та, которая упрощается при интегрировании. Так, в интегралах вида (10) за u необходимо обозначать В интегралах вида (11) и (12) за u необходимо обозначить Пример 10.Найти интеграл
Пример 11.Найти интеграл
Пример 12.Найти интеграл
Пример 13.Найти интеграл Для нахождения этого интеграла метод интегрирования по частям необходимо применить дважды.
Пример 14. Найти интеграл

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 , если существует производная F′(x) при любых x из рассматриваемого промежутка и F′(x) = f(x).
, если существует производная F′(x) при любых x из рассматриваемого промежутка и F′(x) = f(x). . (1)
. (1) . (2)
. (2) (3)
(3) (4)
(4) (5)
(5) где
где 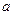 – постоянная. (6)
– постоянная. (6)








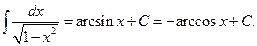
 .
.

 упрощаются с помощью замены
упрощаются с помощью замены  :
:
 (7)
(7)











 т.е. интеграл имеет вид
т.е. интеграл имеет вид  , то его можно упростить с помощью замены переменной
, то его можно упростить с помощью замены переменной  Тогда
Тогда  и получаем:
и получаем:  .
. . (8)
. (8) .
.








 .
.

 .
.
 . (9)
. (9) (10)
(10) (11)
(11) -многочлен степени k,
-многочлен степени k,  .
. (12)
(12) поскольку при дифференцировании этой функции происходит понижении степени (функция «упрощается»).
поскольку при дифференцировании этой функции происходит понижении степени (функция «упрощается»).



 соответственно.
соответственно.



 .
.






