
|
|
Методика изучения понятия «призма», элементов и свойств призмы.Содержание материала в 11 кл.: понятие многогранника; призма, параллелепипед; пирамида, усечённая пирамида; правильные многогранники На изучение материала отводится 17 ч. Цели: уточнить понятие многогранника и сформулировать определение, систематизировать изученные свойства многогранника, изучить новые понятия: наклонная призма (парал-д); высота призмы, пирамиды; произвольная пирамида; правильные многогранники. Особое внимание уделяется правильной призме. Мотивация: необходим для изложения теории объемов; обладают симметрией как многие тела в природе, поэтому имеют практическую значимость; для док-ва важнейших теоритических положений в стереометрии. А. В Погорелов. ПризмаМногогранник сост. из 2-х многоугольников, лежащих в разных плоскостях и совмещ. параллельным переносом и всех отрезков соед. соответствующие точки этих многогр-в. В.В Шлыков.Многогранник у которого 2 грани – равные n – угольники Для запоминания полезно выделить составные элементы определения. Для слабых учащихся достаточно сформулировать определение данное в 10 классе: Призма – это многогранник, у которого 2 грани равные n - угольники, а остальные – параллелограммы. Затем вводим понятие прямой и наклонной призмы. Прямая призма - это призма, у которой боковые ребра перпендикулярны плоскости основания. Другие призмы называются наклонными. Свойства призмы: · Основания призмы являются равными многоугольниками. · Боковые грани призмы являются параллелограммами. · Боковые ребра призмы параллельны и равны. · Объём призмы равен произведению её высоты на площадь основания: V=S*h · Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания. · Площадь боковой поверхности произвольной призмы S=P*l, где P— периметр перпендикулярного сечения, l — длина бокового ребра. · Площадь боковой поверхности правильной призмы S=P*h, где · Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы. · Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах. Параллелепипед рассматривается как частный случай призмы.
Методика изучения понятия «Параллелепипед», его элементов и св-в. Параллелепипед рассматривается как частный случай призмы. Сначала дается само понятие, а затем рассматриваются элементы параллелепипеда. Рекомендуется использовать бумажные модели фигуры. Если основание призмы есть параллелограмм, то она называется параллелепипедом. У параллелепипеда все грани – параллелограммы. Грани параллелепипеда, не имеющие общих вершин, называются противолежащими. Параллелепипед, боковые ребра которого перпендикулярны к плоскости основания, называется прямым параллелепипедом. У него все боковые грани прямоугольники, а основания параллелограммы. Если все грани параллелепипеда – прямоугольники, то его называют прямоугольным параллелепипедом. Длины трех его ребер, которые выходят из одной вершины, называются измерениями прямоугольного параллелепипеда. Свойства параллелепипеда.(Следует обратить внимание учащихся на то, что используются два факта: признак параллельности двух плоскостей и равенство параллелограммов по двум смежным сторонам и углу между ними) Теорема: У параллелепипеда: 1) противолежащие грани равны и параллельны; 2) все четыре диагонали пересекаются в одной точке и делятся в ней пополам. Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. Доказательство: Это выплывает из пространственной теоремы Пифагора. Если

Замечание: в прямоугольном параллелепипеде все диагонали равны.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
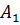 ...
... 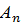 и
и  …
… 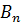 (называются основаниями) соотв. параллельными сторонами
(называются основаниями) соотв. параллельными сторонами  ║
║  )...(
)...(  ║
║  ), а остальные n-граней параллелограммы у каждого из которых 2 стороны являются соответствующими сторонами оснований
), а остальные n-граней параллелограммы у каждого из которых 2 стороны являются соответствующими сторонами оснований — периметр основания призмы,
— периметр основания призмы,  — высота призмы.
— высота призмы.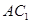 – диагональ прямоугольного параллелепипеда
– диагональ прямоугольного параллелепипеда  , то
, то  – ее проекции на три попарно перпендикулярные прямые (рис. 6). Следовательно,
– ее проекции на три попарно перпендикулярные прямые (рис. 6). Следовательно, 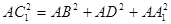 .
.