
|
|
Методологические линии изучения многогранников и их характеристикаВыделяют 2 методологические линии: 1. Классификация многогранников – позволяет уч-ся дать опред соответственных многогранников с помощью родового понятия и видового отличия (Если объем одного понятия входит как часть в объем другого понятия, то первое понятие называется видовым, а второе – родовым.) 2. Изучение количественных характеристик (объем, площадь поверхности) · Классификация многогранников: · Правильные многогранники (Платоновы тела – октаэдр, додекаэдр, икосаэдр, куб, правильный тетраэдр); · Призма (прямая, правильная, куб, наклонная); · Пирамида (правильная, прав тетраэдр); · Усеченная пирамида. По поводу каждого многогранника выясняются вопросы: Определение; Обозначения; Элементы (бок грани, основания, ребра, высоты, поверхность, диагональное сечение); Свойства; Классификация (прямой, наклонный, правильный, неправельный); Построение тела и его сечений и решение з-ч.
Методические особенности изучения пирамид, трудности и пути их устранения. Поскольку наглядные представления о пирамиде давалось уже есть в 10 кл., то учителю остаётся актуализировать знания. Наиболее сложными элементами явл понятие вершины (называют и записывают первой), также высота пирамиды. Учитель должен показать где находятся центры окружностей и какие эти окружности: Если все боковые ребра равны, то: около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр; Если боковые грани наклонены к плоскости основания под одним углом, то: в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр. Должны быть вопросы проверяющие сознательность усвоения при введении правильной пирамиды. Дана пирамида SABC, где ABC – равносторонний треуг. Будет ли она правильной? Особенности для прав пирамиды: - вводится понятие апофемы; - док. свойство в правильной пирамиде, что отрезок соедин. вершину с центром основания явл высотой пирамиды. Что такое центр основания пирамиды? Это центр правильного многоугольника.(многоуг рассм в 9 кл). Можно до её формулир провести практ работу, предложить нарисовать правил пирамиду, найти центр, найти вершину описанной окруж и чем явл данный отрезок для пирамиды. Для того чтобы дать название усеченной пирамиды, можно принести модель пирамиды у которой можно отсечь верхнюю часть плоскости // плоскости основания. Многогранник гранями которого явл два n-угольника и n-четырёх угольников назыв усеченной пирамидой. Па аналогии вводим понятия высоты между // плоскостями. И вводим понятие правильной усеченной пирамиды.
Методика изучения перпендикулярности прямой и плоскости Если 2 прямые перп-ны одной пл-ти,то они паралл-ны.
Признак: Если прямая перп-на 2-ум пересекающимся прямым, лежащим в пл-ти, то она перп-на этой пл-ти. Подвести к формулировке можно, задав вопросы уч-кам о способах задания пл-ти (если анализировать df и вспомнить, чем отлич-ся признак, то достаточно вспомнить задание пл-ти с помощью 2-х перес-ся прямых). С помощью стереометр-ого ящика подвести к необходимости рассм-ния 2-х случаев: прямая проходит через точку пересечения прямых лежащих в пл-ти и не проходит (проводим прямую Д-во признака явл. одним из наиболее сложных, поэтому: 1) Иметь каркасную модель 2) Подготовить таблицу 3) Компьютерная анимация с последующим показом готового рисунка на доске или таблице. Дополнительные построения должен подсказать учитель. Последующий поиск док-ва по след.схеме: 1)OL–медиана треуг-каABL, 2) PL-общая, AP=B, сл-но AQ=BQ,сл-но Док-во запис-ся в обратном порядке и может быть предложен след.план: 1. AP=BP, AQ=BQ 2. 3. 4. Для док-ва многих утв-ний в данной теме исп-ся теоремы о сущ-нии и ед-ти пл-ти перп-ной данной прямой и обратная ей.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 через точку пересечения, тогда
через точку пересечения, тогда  ).
). , если тр-кABL–равнобедр,т.е.AL=BL – ?
, если тр-кABL–равнобедр,т.е.AL=BL – ?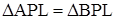 – ?
– ? (по 3-м сторонам)
(по 3-м сторонам) (по 2-м катетам).
(по 2-м катетам).
 –равнобедр.,т.к.AL=LB,LO-медиана,сл-но LO-высота,
–равнобедр.,т.к.AL=LB,LO-медиана,сл-но LO-высота,