Понятие определённого интеграла, его геометрический смысл. Свойства определённого интеграла
5.1. Понятие определённого интеграла, его геометрический смысл
Пусть функция  определена на определена на  . Разобьём . Разобьём  произвольным образом точками произвольным образом точками  на на  частичных отрезков длиной частичных отрезков длиной  . Выберем в каждом из них произвольно точку . Выберем в каждом из них произвольно точку  и найдем значения функции в каждой из этих точек и найдем значения функции в каждой из этих точек 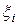 , то есть , то есть  . Сумма вида . Сумма вида
 (5.1) (5.1)
называется n-ой интегральной суммой функции  на на  . .
 Геометрический смысл интегральной суммы (5.1) – сумма площадей прямоугольников с основаниями Геометрический смысл интегральной суммы (5.1) – сумма площадей прямоугольников с основаниями  и высотами и высотами  (рис.1). Обозначим через (рис.1). Обозначим через  длину наибольшего частичного отрезка данного разбиения длину наибольшего частичного отрезка данного разбиения  . Найдем предел интегральной суммы . Найдем предел интегральной суммы  , когда , когда  так, что так, что  . .
Определение. Если существует конечный предел  суммы (5.1), не зависящий от способа разбиения отрезка суммы (5.1), не зависящий от способа разбиения отрезка  на частичные отрезки и выбора в них точек на частичные отрезки и выбора в них точек  , то этот предел называется определённым интегралом от функции , то этот предел называется определённым интегралом от функции  по отрезку по отрезку  и обозначается: и обозначается:  . .
 , ,
 – подынтегральная функция, – подынтегральная функция,  – подынтегральное выражение, – подынтегральное выражение,  – отрезок интегрирования, – отрезок интегрирования,  и и  – нижний и верхний пределы интегрирования, – нижний и верхний пределы интегрирования,  – переменная интегрирования. – переменная интегрирования.
Теорема. Если функция  непрерывна на непрерывна на  , то она интегрируема на , то она интегрируема на  , т.е. предел интегральной суммы (5.1) существует. , т.е. предел интегральной суммы (5.1) существует.
Если  , то геометрически определённый интеграл выражает площадь фигуры, ограниченной графиком функции , то геометрически определённый интеграл выражает площадь фигуры, ограниченной графиком функции  , осью , осью  и прямыми и прямыми   . Эта фигура называется криволинейной трапецией. . Эта фигура называется криволинейной трапецией.
В общем случае, когда функция  на отрезке на отрезке  принимает значения разных знаков, определённый интеграл выражает разность площадей криволинейных трапеций, расположенных над осью принимает значения разных знаков, определённый интеграл выражает разность площадей криволинейных трапеций, расположенных над осью  и под ней, т.к. и под ней, т.к.  расположенной под осью расположенной под осью  , принимает отрицательное значение. , принимает отрицательное значение.
5.2. Свойства определённого интеграла
Далее будем рассматривать функцию  непрерывную на непрерывную на  . По определению полагают, что определённый интеграл от функции с равными верхним и нижним пределами интегрирования равен нулю . По определению полагают, что определённый интеграл от функции с равными верхним и нижним пределами интегрирования равен нулю
 . (5.2) . (5.2)
1. При перестановке пределов интегрирования определённый интеграл меняет знак на противоположный
 . (5.3) . (5.3)
2. Аддитивность по области интегрирования.
Каковы бы ни были числа  , если , если  интегрируема на большем из отрезков, концами которых являются эти точки, то интегрируема на большем из отрезков, концами которых являются эти точки, то  интегрируема и на меньших отрезках иимеет место равенство интегрируема и на меньших отрезках иимеет место равенство
 . (5.4) . (5.4)
Доказательство. Пусть  , т.к. предел интегральной суммы не зависит от способа разбиения , т.к. предел интегральной суммы не зависит от способа разбиения  , то будем разбивать , то будем разбивать  так, чтобы точка с была точкой разбиения, т.е. так, чтобы точка с была точкой разбиения, т.е.  , тогда , тогда  . Переходя к пределу при . Переходя к пределу при  , получаем равенство (5.4). , получаем равенство (5.4).
Далее пусть  , тогда по доказанному , тогда по доказанному 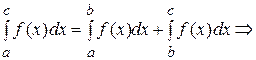  . .
3. Постоянный множитель можно вынести за знак определённого интеграла, т.е.
 . (5.5) . (5.5)
4. Определённый интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т.е.
 . (5.6) . (5.6)
Доказательство. Очевидно, что
 , переходя к пределу, получим , переходя к пределу, получим 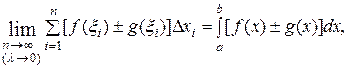

Итак,  . .
Свойство 4 распространяется на сумму любого конечного числа слагаемых.
Свойства 3,4 называются свойствами линейности.
Далее будем считать, что  . .
5. Если всюду на  верно неравенство верно неравенство  , то , то  . .
6. Монотонность.
Если всюду на  верно неравенство верно неравенство  , то , то
 . .
7. Оценка модуля интеграла.
Модуль определенного интеграла не превосходит интеграла от модуля подынтегральной функции, то есть
 . (5.7) . (5.7)
Следствие.Если всюду на  верно неравенство верно неравенство  , то , то  . .
8. Если  и и  – соответственно наименьшее и наибольшее значения функции – соответственно наименьшее и наибольшее значения функции  на на  , то , то
 . (5.8) . (5.8)
9. Теорема о среднем.
На отрезке  существует точка существует точка  такая,что такая,что
 . (5.9) . (5.9)
Доказательство. Пусть  , так что , так что  для любых для любых  . Тогда в силу монотонности и линейности определённого интеграла имеем: . Тогда в силу монотонности и линейности определённого интеграла имеем:
 и, разделив на и, разделив на  , получаем , получаем  . Так какнепрерывная на отрезке функция принимает все промежуточные значения между наибольшим и наименьшим, то найдётся по крайней мере одна точка . Так какнепрерывная на отрезке функция принимает все промежуточные значения между наибольшим и наименьшим, то найдётся по крайней мере одна точка  на отрезке на отрезке  такая, что такая, что   . Число . Число  называется средним значением функции называется средним значением функции  на отрезке на отрезке  . .
9¢. Обобщенная теорема о среднем для интегралов.
Если функция  интегрируема и неотрицательна на отрезке интегрируема и неотрицательна на отрезке  , а функция , а функция  удовлетворяет на этом отрезке условию удовлетворяет на этом отрезке условию  , где , где  и и  , то , то
 . .
10. Интеграл с переменным верхним пределом.Если функция  определена и дифференцируема на определена и дифференцируема на  и имеет место равенство и имеет место равенство  , то , то  – первообразная для функции – первообразная для функции  . .
11. Формула Ньютона-Лейбница.Если 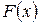 – первообразная функции – первообразная функции  на на  , то , то
 . (5.10) . (5.10)
Доказательство. Наряду с 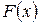 первообразной функции первообразной функции  является функция является функция  . А т.к. всякие две первообразные одной и той же функции отличаются на константу, то справедливо равенство: . А т.к. всякие две первообразные одной и той же функции отличаются на константу, то справедливо равенство:  . Полагая в этом равенстве сначала . Полагая в этом равенстве сначала  , а затем , а затем  , получим , получим  , ,  . Вычитая из первого равенства второе, получим формулу Ньютона-Лейбница. Разность в правой части этой формулы записывают также в виде . Вычитая из первого равенства второе, получим формулу Ньютона-Лейбница. Разность в правой части этой формулы записывают также в виде  . .
Формула (5.10) даёт простой метод вычисления определённого интеграла: определённый интеграл от непрерывной функции равен разности значений любой её первообразной, вычисленных для верхнего и нижнего пределов интегрирования. Таким образом, задача вычисления определённого интеграла сводится к нахождению неопределённого интеграла. Здесь используются те же методы интегрирования.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 определена на
определена на  . Разобьём
. Разобьём  на
на  частичных отрезков длиной
частичных отрезков длиной  . Выберем в каждом из них произвольно точку
. Выберем в каждом из них произвольно точку  и найдем значения функции в каждой из этих точек
и найдем значения функции в каждой из этих точек 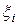 , то есть
, то есть  . Сумма вида
. Сумма вида (5.1)
(5.1) на
на  Геометрический смысл интегральной суммы (5.1) – сумма площадей прямоугольников с основаниями
Геометрический смысл интегральной суммы (5.1) – сумма площадей прямоугольников с основаниями  и высотами
и высотами  (рис.1). Обозначим через
(рис.1). Обозначим через  длину наибольшего частичного отрезка данного разбиения
длину наибольшего частичного отрезка данного разбиения  . Найдем предел интегральной суммы
. Найдем предел интегральной суммы  , когда
, когда  так, что
так, что  .
. суммы (5.1), не зависящий от способа разбиения отрезка
суммы (5.1), не зависящий от способа разбиения отрезка  , то этот предел называется определённым интегралом от функции
, то этот предел называется определённым интегралом от функции  по отрезку
по отрезку  .
. ,
, – подынтегральное выражение,
– подынтегральное выражение,  и
и  – нижний и верхний пределы интегрирования,
– нижний и верхний пределы интегрирования,  – переменная интегрирования.
– переменная интегрирования. , то геометрически определённый интеграл выражает площадь фигуры, ограниченной графиком функции
, то геометрически определённый интеграл выражает площадь фигуры, ограниченной графиком функции  и прямыми
и прямыми 
 . Эта фигура называется криволинейной трапецией.
. Эта фигура называется криволинейной трапецией. расположенной под осью
расположенной под осью  . (5.2)
. (5.2) . (5.3)
. (5.3) , если
, если  . (5.4)
. (5.4) , т.к. предел интегральной суммы не зависит от способа разбиения
, т.к. предел интегральной суммы не зависит от способа разбиения  , тогда
, тогда  . Переходя к пределу при
. Переходя к пределу при  , тогда по доказанному
, тогда по доказанному 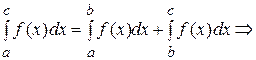
 .
. . (5.5)
. (5.5) . (5.6)
. (5.6) , переходя к пределу, получим
, переходя к пределу, получим 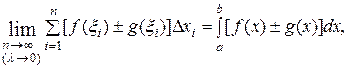

 .
. , то
, то  .
. , то
, то .
. . (5.7)
. (5.7) , то
, то  .
. и
и  – соответственно наименьшее и наибольшее значения функции
– соответственно наименьшее и наибольшее значения функции  . (5.8)
. (5.8) такая,что
такая,что . (5.9)
. (5.9) , так что
, так что  для любых
для любых  . Тогда в силу монотонности и линейности определённого интеграла имеем:
. Тогда в силу монотонности и линейности определённого интеграла имеем: и, разделив на
и, разделив на  , получаем
, получаем  . Так какнепрерывная на отрезке функция принимает все промежуточные значения между наибольшим и наименьшим, то найдётся по крайней мере одна точка
. Так какнепрерывная на отрезке функция принимает все промежуточные значения между наибольшим и наименьшим, то найдётся по крайней мере одна точка 
 . Число
. Число  называется средним значением функции
называется средним значением функции  интегрируема и неотрицательна на отрезке
интегрируема и неотрицательна на отрезке  , где
, где  и
и  , то
, то .
. определена и дифференцируема на
определена и дифференцируема на  , то
, то  – первообразная для функции
– первообразная для функции 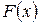 – первообразная функции
– первообразная функции  . (5.10)
. (5.10) . А т.к. всякие две первообразные одной и той же функции отличаются на константу, то справедливо равенство:
. А т.к. всякие две первообразные одной и той же функции отличаются на константу, то справедливо равенство:  . Полагая в этом равенстве сначала
. Полагая в этом равенстве сначала  , а затем
, а затем  , получим
, получим  ,
,  . Вычитая из первого равенства второе, получим формулу Ньютона-Лейбница. Разность в правой части этой формулы записывают также в виде
. Вычитая из первого равенства второе, получим формулу Ньютона-Лейбница. Разность в правой части этой формулы записывают также в виде  .
.