
|
|
Примеры решения типовых задач12 Примеры решения типовых задач
Пример 1.Вычислить интеграл Решение. Воспользуемся свойствами 3 и 4 и табличными интегралами (5), (2), (3), (9). Получим:
Пример 2. Вычислить интеграл Решение. Возведём в квадрат подынтегральную функцию, проведём тригонометрические преобразования, применим свойство 4 и табличные интегралы (2),(5)
Пример 3. Вычислить интеграл Решение. Применив тождественные преобразования, свойство 4 и табличные интегралы (2), (10), получим:
Пример 4.Вычислить интеграл Решение. Введём переменную
При замене переменной в неопределённом интеграле иногда более удобно заменять не Пример5. Вычислить интеграл Решение. Положим
Пример 6. Вычислить интеграл Решение. Применим известное тригонометрическое тождество, далее положим
Пример 7. Вычислить интеграл Решение. Положим
Пример 8. Вычислить интеграл Решение. Положим
Пример 9. Вычислить интеграл Решение. Положим
В некоторых случаях формулу интегрирования по частям необходимо применять несколько раз. Пример 10.Вычислить интеграл Решение. Положим
Задания для самостоятельной работы
n 1. Вычислить интегралы.
n 2. Вычислить интегралы с помощью метода замены переменной.
n 3. Вычислить интеграл методом интегрирования по частям.
Интегрирование рациональных функций
Рациональными функциями называются функции вида Число Теорема Безу.Многочлен Таким образом, Например: Будем рассматривать правильные рациональные дроби с действительными коэффициентами многочленов в числителе и знаменателе. Среди них назовём простейшими дроби вида: Теорема (о разложении правильной дроби в сумму простейших дробей). Всякую рациональную правильную дробь со знаменателем представимым в виде произведения можно разложить в виде суммы простейших рациональных дробей типа 1) – 2). В данном разложении каждому корню
Примеры решения типовых задач Рассмотрим два наиболее простых способа нахождения неопределённых коэффициентов на одном конкретном примере. Пример 1. Вычислить интеграл Решение. I метод – метод неопределённых коэффициентов. Разложим знаменатель на линейные и квадратичные множители с действительными коэффициентами: Приравниваем коэффициенты при одинаковых степенях При При При Тогда Далее находим неопределённый интеграл:
II метод – метод частных значений. Придадим аргументу
Пример 2. Вычислить интеграл Решение. Представим дробь в виде суммы простейших дробей с неопределёнными коэффициентами: Пример 3.Вычислить интеграл Решение. Выделим целую часть дроби:
Разложим знаменатель дроби на множители с действительными коэффициентами:
При При При
Задания для самостоятельной работы
n 4. Вычислить интеграл от дроби, содержащий в знаменателе квадратный трехчлен.
n 5. Вычислить интегралы от рациональных функций.
4. Интегрирование некоторых тригонометрических и
В этом параграфе для интегралов от некоторых классов тригонометрических и иррациональных выражений будут даны рационализирующие подстановки, то есть замены переменной, приводящие исходный интеграл к интегралу от рациональной дроби. Здесь через 4.1. Интегрирование тригонометрических функций
I. Интегралы вида Подставляя в подынтегральное выражение вместо
В случае, когда имеет место тождество
Если Если II. Для отыскания интегралов вида
При нахождении интегралов вида 1) хотя бы одно из чисел
2) оба числа
4.2. Интегрирование некоторых иррациональных функций
Не для всякой иррациональной функции можно найти первообразную в виде элементарной функции. Рассмотрим интегралы от некоторых иррациональных функций, которые с помощью определённых подстановок приводятся к интегралам от рациональных функций новой переменной. I. Интеграл вида II. Интегралы вида
К рассмотренным интегралам могут быть преобразованы интегралы Если в трехчлене Возведя обе части равенства
Если же в трехчлене

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.

 .
.
 .
.

 .
.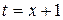 ,
,  . Тогда
. Тогда  . Используем формулу (2.1)
. Используем формулу (2.1)
 .
. как функцию
как функцию  , а наоборот, задавать
, а наоборот, задавать  .
. . Тогда
. Тогда  . Используя формулу (2.1) и табличный интеграл (3), получим:
. Используя формулу (2.1) и табличный интеграл (3), получим: .
.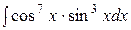 .
. . Тогда
. Тогда  . Используя табличный интеграл (2), имеем:
. Используя табличный интеграл (2), имеем: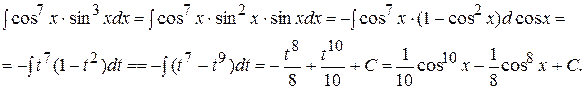

 .
. . Тогда
. Тогда  и по формуле интегрирования по частям получим:
и по формуле интегрирования по частям получим:
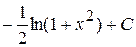 , где
, где  .
. .
. Тогда
Тогда  и по формуле интегрирования по частям получим:
и по формуле интегрирования по частям получим: .
.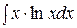 .
. . Тогда
. Тогда  и по формуле интегрирования по частям получим:
и по формуле интегрирования по частям получим: .
. .
. . Тогда
. Тогда  , по формуле интегрирования по частям имеем:
, по формуле интегрирования по частям имеем:  . Далее, пусть
. Далее, пусть  . Тогда
. Тогда  , ещё раз применив формулу интегрирования по частям, имеем:
, ещё раз применив формулу интегрирования по частям, имеем: 
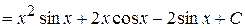 .
. ;
;
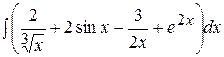 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
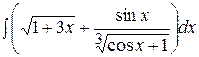 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
 ,
, 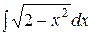 ;
;
 ,
, 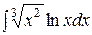 ;
;
 ,
,  ;
;
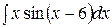 ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
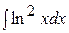 ,
,  ;
;
 ,
, 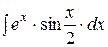 ;
;
 ,
,  ;
;
 ,
,  .
.
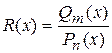 , где
, где  – многочлены степени
– многочлены степени  соответственно. Приведём необходимые в дальнейшем сведения из алгебры о рациональных функциях.
соответственно. Приведём необходимые в дальнейшем сведения из алгебры о рациональных функциях. называется корнем или нулём многочлена
называется корнем или нулём многочлена 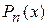 , если
, если 
 тогда и только тогда, когда число а является корнем данного многочлена.
тогда и только тогда, когда число а является корнем данного многочлена.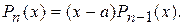 Корень а называется k-кратным, если
Корень а называется k-кратным, если  , где
, где 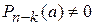 . Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя. В противном случае называется неправильной. Всякую неправильную рациональную дробь можно, деля числитель на знаменатель, представить в виде суммы многочлена, называемого целой частью дроби, и правильной рациональной дроби.
. Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя. В противном случае называется неправильной. Всякую неправильную рациональную дробь можно, деля числитель на знаменатель, представить в виде суммы многочлена, называемого целой частью дроби, и правильной рациональной дроби. .
. ,
, 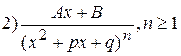 ,
,  .
. кратности
кратности  многочлена
многочлена  , где
, где  – действительные числа, называемые неопределёнными коэффициентами.
– действительные числа, называемые неопределёнными коэффициентами. .
. и запишем разложение данной дроби на простейшие с неопределёнными коэффициентами:
и запишем разложение данной дроби на простейшие с неопределёнными коэффициентами:  . Приведя к общему знаменателю правую часть, получим равенство числителей:
. Приведя к общему знаменателю правую часть, получим равенство числителей:  .
.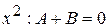 .
. .
.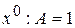 .
. и
и  .
.
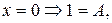

 ,
, . Тогда получим систему независимых уравнений, из которой имеем:
. Тогда получим систему независимых уравнений, из которой имеем:  .
. .
. . Приведя дроби в обеих частях к общему знаменателю, получим:
. Приведя дроби в обеих частях к общему знаменателю, получим: 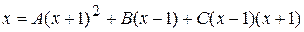 . Найдём неопределённые коэффициенты методом частных значений, придадим аргументу
. Найдём неопределённые коэффициенты методом частных значений, придадим аргументу  , откуда
, откуда  и
и  . Таким образом:
. Таким образом: 
 .
. .
. .
. . Умножая это равенство на общий знаменатель, получим:
. Умножая это равенство на общий знаменатель, получим:  . Приравняем коэффициенты при одинаковых степенях
. Приравняем коэффициенты при одинаковых степенях  .
. .
.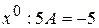 . Тогда
. Тогда  и
и . Итак, вычислим неопределённый интеграл:
. Итак, вычислим неопределённый интеграл: 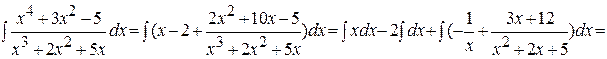


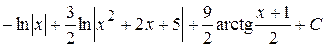 .
.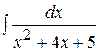
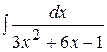 ;
;
 ;
;
 ;
;
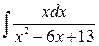 ;
;
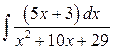 ;
;
 ;
;
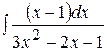 ;
;
 ;
;
 .
.
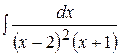 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
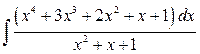 ;
;
 ;
;
 ;
;
 .
.
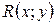 будем обозначать рациональные выражения относительно
будем обозначать рациональные выражения относительно  , то есть выражения, полученные путем применения конечного числа раз к аргументам
, то есть выражения, полученные путем применения конечного числа раз к аргументам  приводятся к интегралам от рациональной функции новой переменной
приводятся к интегралам от рациональной функции новой переменной 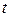 с помощью универсальной тригонометрической подстановки
с помощью универсальной тригонометрической подстановки .В этом случае
.В этом случае 
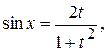

 .
.

 их выражения через
их выражения через 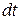 получим интеграл от рациональной дроби:
получим интеграл от рациональной дроби: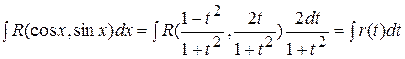 .
. для приведения подынтегральной функции к рациональному виду можно применять упрощённую подстановку
для приведения подынтегральной функции к рациональному виду можно применять упрощённую подстановку  .При этом
.При этом  .
. – нечетная функция относительно
– нечетная функция относительно 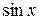 , т.е.
, т.е.  , то интеграл рационализируется подстановкой
, то интеграл рационализируется подстановкой  .
. , т.е.
, т.е.  , то интеграл рационализируется подстановкой
, то интеграл рационализируется подстановкой 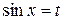 .
.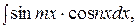

 используют следующие формулы:
используют следующие формулы:



 возможны следующие случаи:
возможны следующие случаи: или
или  – нечетное, например
– нечетное, например  , тогда
, тогда 

 ,
, 
 , где
, где  – постоянные,
– постоянные,  приводятся к интегралу от рациональной функции новой переменной
приводятся к интегралу от рациональной функции новой переменной  с помощью подстановки
с помощью подстановки  , где
, где  наименьшее общее кратное (НОК) знаменателей дробей
наименьшее общее кратное (НОК) знаменателей дробей 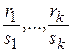 , т.е.
, т.е.  .
.

 тригонометрическими подстановками соответственно
тригонометрическими подстановками соответственно 

 сводятся к уже рассмотренным интегралам вида
сводятся к уже рассмотренным интегралам вида  , если из квадратного трёхчлена выделить полный квадрат суммы и сделать линейную замену переменной.
, если из квадратного трёхчлена выделить полный квадрат суммы и сделать линейную замену переменной.
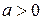 , то интеграл рационализируется подстановкой Эйлера
, то интеграл рационализируется подстановкой Эйлера 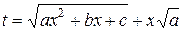 .
. в квадрат, получаем
в квадрат, получаем  ,
,  ,
,  ,
,  .Таким образом,
.Таким образом, 
 , где
, где  – рациональная функция от
– рациональная функция от  , а
, а 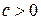 , то для рационализации интеграла можно применить другую подстановку Эйлера:
, то для рационализации интеграла можно применить другую подстановку Эйлера:  .
.