
|
|
Формулировка принципа оптимальности Беллмана.Оптимальное поведение обладает тем свойством, что каковыми бы не были первоначальные решения, и первоначальные состояния в начальный момент времени, последующие решения (то есть управления) должны составлять оптимальное поведение относительно состояния, получающегося в результате первого решения. Если вы не используете наилучшим образом то, чем вы располагаете, то вы никогда не распорядитесь наилучшим образом и тем, что вы могли иметь в дальнейшем.
На рисунке 1 дана иллюстрация этого принципа на примере задачи с одной фазовой координатой x. Кривая Предположим, что общая задача управления имеет вид: Найти
Максимальное значение целевого функционала задачи с начальным состоянием
и назовем эту функцию – функцией оптимального поведения. Отметим, что в то время как Тем самым наша исходная задача (1)является “погруженной” в более высокий класс задач, характеризуемый значениями
Если
Значение ФОП на всем интервале времени начинающимся в момент времени
В динамическом программировании существенную роль играет предположения относительно функции ФОП: 1)Однозначная функция, 2) Непрерывно дифференцируемая функция от Предположив это, можно в окрестности точки
Подставляя (5)в (4), получаем:
Рассмотрим предел следующего выражения:
Из (1):
Уравнение (8)является основным дифференциальным уравнением в частных производных, используемым в динамическом программировании. Оно называется уравнением Беллмана. Так как второй член в квадратных скобках уравнения (8)представляет собой скалярное произведение вектора
С уравнением связано, в качестве граничного условия, ограничение, накладываемое на конечное состояние:
Это условие показывает, что значение ФОП для задачи с начальным моментом и начальным состоянием, которые являются соответственно конечный момент времени
В общем случае это уравнение в частных производных первого порядка, как правило, не линейное. Как правило, не линейное уравнение не имеет аналитического решения. Следовательно, необходимо применять какие – либо численные методы решения. Это уравнение Беллмана можно представить в виде разносных схем для использования на ЭВМ. Но современные ЭВМ не позволяют найти решение с большой размерностью. Для решения задач Динамического программирования, память ЭВМ должна содержать Если, например, каждую фазовую координату разбить на 100 значений, а 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
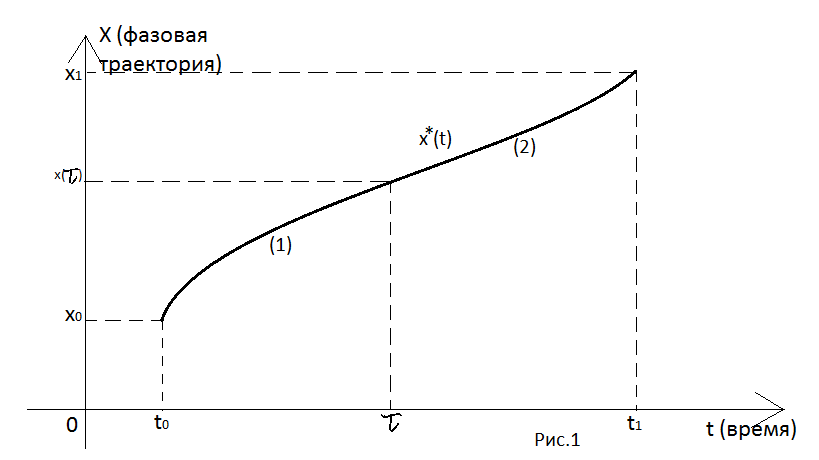
 - соответствующая оптимальная траектория. При этом предполагается, что начальное состояние и конечное фиксировано (задача с фиксированными концами). Вся траектория разделена на две части (1) и (2), относительно момента времени
- соответствующая оптимальная траектория. При этом предполагается, что начальное состояние и конечное фиксировано (задача с фиксированными концами). Вся траектория разделена на две части (1) и (2), относительно момента времени 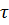 . Согласно принципу оптимальности Беллмана траектория (2) , определенная при
. Согласно принципу оптимальности Беллмана траектория (2) , определенная при  , должна представлять собой оптимальную траекторию по отношению к начальному состоянию
, должна представлять собой оптимальную траекторию по отношению к начальному состоянию  . Следовательно, часть (2) оптимальной траектории сама по себе должна быть оптимальной траекторией, в независимости от того, как она пришла в состояние, являющиеся начальным состоянием для части (2) траектории.
. Следовательно, часть (2) оптимальной траектории сама по себе должна быть оптимальной траекторией, в независимости от того, как она пришла в состояние, являющиеся начальным состоянием для части (2) траектории. , (1)
, (1) ,
, ,
,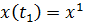 ,
,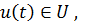
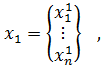
 .
. и начальным моментом времени
и начальным моментом времени 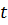 обозначим
обозначим (2)
(2) представляет собой функционал, зависящий от управления
представляет собой функционал, зависящий от управления  , то
, то 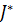 - является функцией зависящей от
- является функцией зависящей от  параметра:
параметра:  , (3)
, (3) 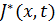 является функцией ФОП с начальным состоянием
является функцией ФОП с начальным состоянием 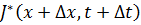 – будет ФОП для второй части оптимальной траектории с начальным моментом времени
– будет ФОП для второй части оптимальной траектории с начальным моментом времени 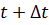 и начальным состоянием
и начальным состоянием  . Поскольку прирост ФОП на протяжении всего промежутка времени между
. Поскольку прирост ФОП на протяжении всего промежутка времени между  .
.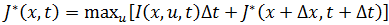 , (4)
, (4)  ФОП разложить в ряд Тейлора:
ФОП разложить в ряд Тейлора: (5)
(5)
 .
.  ,
, ,
, ,
, . (7)
. (7) , тогда
, тогда ,
, . (8)
. (8) 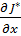 и вектора - столбца
и вектора - столбца  , то уравнение можно записать следующим образом:
, то уравнение можно записать следующим образом: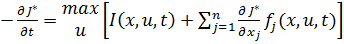 (9)
(9)  . (10)
. (10)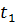 и конечное состояние
и конечное состояние  . Если бы уравнение Беллмана было решено, то мы получили бы ФОП, и, следовательно, оптимальное значение целевой функции для исходной задачи можно было бы определить как частное значение функции
. Если бы уравнение Беллмана было решено, то мы получили бы ФОП, и, следовательно, оптимальное значение целевой функции для исходной задачи можно было бы определить как частное значение функции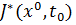 .
. - ячеек памяти, где
- ячеек памяти, где 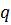 - размер сетки (число дискретных значений) применяющихся каждой фазовой координатой.
- размер сетки (число дискретных значений) применяющихся каждой фазовой координатой. , то память должна состоять из 100мил ячеек. Это трудно реализовать на ЭВМ. Беллман назвал это препятствие – “проклятие размерности”.
, то память должна состоять из 100мил ячеек. Это трудно реализовать на ЭВМ. Беллман назвал это препятствие – “проклятие размерности”.