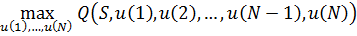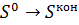|
|
Специфика метода динамического программирования.Министерство образование и науки Российской Федерации Московский Авиационный Институт (Национальный Исследовательский Университет)
Факультет № 1: ”Авиационная техника”. Кафедра: “Внешнее проектирование и эффективность авиационных комплексов”. Специальность: ”Моделирование и исследование операций в организационно – технических системах”.
Курсовая работа По Численному моделированию задач специальности. “Решение целочисленной задачи нелинейного программирования методом динамического программирования ”.
Выполнилстудент гр.01-316 Секретарёв Максим Дмитриевич ПринялГорлов Валентин Михайлович
Москва
Содержание 1)Постановка задачи………………………………………………………стр.2 2)Теория………………………………………………………………………….стр.3 Технология системного моделирования…………………..стр.3 А)Динамическое программирование………………….…стр.3 Б)Специфика метода динамического программирования…………………………………………….стр.4 В)Сущность подхода динамического программирования……………………………………………..стр.5 Г)Принцип оптимальности и уравнение Беллмана………………………………………………………………стр.6 Е)Решение многошаговых задач оптимизации методом динамического программирования..…стр.10 3)Решение поставленной задачи………………………………….стр.15 4)Решение контрольного варианта………………………………стр.19 5)Решение поставленной задачи, с измененными исходными данными…………………………………………………….стр.21
Постановка задачи. Вариант №9. Решить задачу методом динамического программирования. Составить оптимальный план использования Пусть
Необходимо максимизировать
Исходные данные:
Для проверки сделать контрольный расчет для варианта (из лекций). Сделать расчеты для заданного
Теория. Технология системного моделирования. Динамическое программирование. В пятидесятые годы прошлого века был развит новый общий метод решения оптимизационных задач динамического программирования. Динамическое программирование представляет собой математический метод оптимизации решений, приспособленный для исследования многошаговых (многоэтапных) операций. Рассмотрим некоторую физическую систему, которая может с течением времени менять свое состояние. Пусть в любой момент времени ей соответствует некоторый вектор состояния Будем считать, что система из одного состояния в другое переходит за счет управления. То есть всю систему мероприятий, с помощью которой система меняет свое состояние во времени, обозначим вектором С процессом изменения состояния
Для постановки задачи оптимизации необходимо еще учесть условия, накладываемые на начальное состояние В других задачах эти состояния могут быть ограничены заданием области начальных данных (состояний)
В общем виде задача оптимального управления формулируется следующим образом: Из множества возможных уравнений Специфика метода динамического программирования. Специфика метода динамического программирования заключается в том, что задача отыскания ОУ Идея метода заключается в том, что бы отыскания максимума сложной функции многих переменных свести к операции - последовательной максимизации функции одной переменной. То есть вместо того, что бы один раз решать сложную задачу, мы предпочитаем много раз решать задачу относительно более простую.
В основе метода динамического программирования лежит принцип оптимальности, сформулированный Беллманом Р. для широкого круга процессов или систем, сформулированный следующим образом: Оптимальная стратегия обладает тем свойством, что каковыми бы не были начальные состояния и начальные решения, последующие решение должно составлять оптимальную стратегию лишь относительно состояния рассматриваемое в данный момент времени. Другими словами оптимальная стратегия не зависит от “предыстории” системы и определяется ее состоянием в данный момент времени. Принцип оптимальности динамического программирования не предполагает, что выбирая управление на данном шаге можно забыть обо всех остальных. Напротив, управление на каждом шаге должно выбираться с учетом его последствий. Общее правило формулирования управления таково: в процессе многошагового планирования управление на каждом шаге должно приниматься с учетом “будущего”, однако среди всех шагов существует такой, на который это правило не распространяется. На последний шаг, единственный из всех, можно планировать так, что бы он приносил наибольшее приращение критерия Спланировав его оптимально, можно к нему “пристроить” предпоследний, к этому в свою очередь еще предпоследний, и.т.д. Поэтому процесс динамического программирования удобно разворачивать в возвратном времени. То есть с конца процесса к началу. Оптимальное управление на предпоследнем шаге зависит от того, каково было возможное состояние оптимального управления на последнем шаге. Необходимо выбрать такое управление, которое переводило бы систему в конечное состояние
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
однотипных поисковых средств, если задана вероятность 
обнаружение объекта в 
– ом районе одним поисковым средством. Известно, что объект может находиться в одном из районов поиска с вероятностью 
.
- количество средств, назначаемых в 
, а математическое ожидание обнаружения объекта определяется:
.
при ограничениях:
,
.
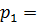
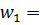
, для 
и 
. Результаты свести в таблицу.
. Обычно вектор 
– многомерный, состоящий из конечного набора величин 
– называемых переменными состояния.
. Вектор 
, то есть ее состояние, изменилось в некотором заранее предписанном образе.
, который зависит от состояния системы 
.
и конечное состояние 
. В простейшем случае оба эти состояния полностью заданы.
и области конечных значений 
.
, которое переводит систему из начального состояния 
принимал максимальное значение.
.
и при этом позволяло бы получить максимальное приращение функции 
шаге зависит от того, какие оптимальные шаги были сделаны на предыдущих шагах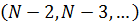 
. Планирование управления в динамическом программировании зависит от того, какие управления были выбраны на предыдущих шагах 
.
