
|
|
Достаточные условия экстремума.Пусть
Разложим функцию в ряд Тейлора в окрестности стационарной точки.
(При этом Обозначая
В силу того, что второе слагаемое в скобках бесконечно мало по сравнению с первым, знак приращения
В алгебре: Def. Вещественно значная функция векторного аргумента Из определения квадратичной формы ясно, что второй дифференциал функции является квадратичной формой Def. Квадратичная форма Def. Квадратичная форма Def. Квадратичная форма называется полуопределённой, если (или Def. Квадратичная форма называется неопределённой, если
Критерий Сильвестра : Для того чтобы квадратичная форма была положительно определённой необходимо и достаточно, чтобы все главные миноры матрицы квадратичной формы были положительны. Для того чтобы квадратичная форма была отрицательно определённой необходимо и достаточно чтобы главные миноры матрицы квадратичной формы чередовались по знаку начиная с минуса: Если миноры будут ++++… или –+–+… но среди них встречаются нулевые то форма будет полуопределённой. Δ▲. Пример: Форма А= Все миноры положительны, форма положительно определена . В самом деле, нетрудно проверить, что:
Т°.Если квадратичная форма будет положительно определённой то функция, в испытуемой точке, функция будет иметь минимум; если отрицательно определённой то функция будет иметь максимум. Если форма полуопределена, то для ответа на вопрос о экстремуме функции требуется привлечение производных более высокого порядка. Во всех остальных случаях – экстремума нет. Δ▲. Примеры: 1°. Исследовать на экстремум функцию: Необходимые условия экстремума:
Достаточные условия экстремума: составим матрицу из вторых производных:
Функция в точке (0,0) имеет минимум. Впрочем, это ясно если построить линии уровня функции, u = const:
2°. Необходимые условия экстремума: Достаточные условия экстремума:
при этом ясно, что на линии
Наибольшие и наименьшие значения функции В замкнутой области.
Пусть функция Чтобы найти наибольшее и наименьшее значение функции в замкнутой ограниченной области D нужно найти все внутренние точки D «подозрительные» на экстремум и сравнить со значениями функции в граничных точках области. Наибольшее (наименьшее) из этих значений и будет наибольшим (наименьшим) значением функции в области. Примеры: 1°.Найти наибольшее значение функции Получаем: Наибольшее значение функции u(x,y):
20. Найти наибольшее и наименьшее значение функции:
а). Из условия:
Найти наибольшее и наименьшее значение функции
Из необходимых условий следует, что: а1). x = 0, y = 0; ( а3). y = 0; x = Последняя система, очевидно, решений не имеет.
б).Теперь надо посмотреть функцию x2 + y2 = 1 Þ y2 = 1 – x2 Þ Для нее: б1). x = 0; (
в). И, наконец, надо посмотреть точки x = ±1 при этом в1). x = ± 1, (
Вывод: наибольшее значение функции в области наименьшее значение
3°. Для функции одного переменного, если внутри промежутка имелось только одна точка локального экстремума, то в ней обязательно достигалось наименьшее либо наибольшее значение. Для функций многих переменных это, вообще говоря, не так. Δ. Для примера рассмотрим функцию Отсюда следует: а1). x = 0, y = 0. а2). x = 2, y = 2 – не принадлежат прямоугольнику. Достаточное условие экстремума в точке (0,0):
Функция

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 определена, непрерывна и имеет непрерывные производные первого и второго порядка в некоторой окрестности стационарной точки
определена, непрерывна и имеет непрерывные производные первого и второго порядка в некоторой окрестности стационарной точки 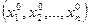 . Тогда:
. Тогда:
 =
= 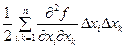 .
.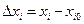 .
. 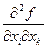 – вычислены в точке
– вычислены в точке  ,
, 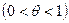 .
.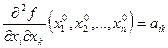 , получим
, получим 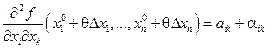 , где
, где при
при  , и, следовательно,
, и, следовательно,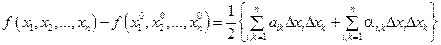 .
.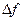 определяется знаком второго дифференциала функции (если он не обращается в нуль). Следовательно от знака второго дифференциала зависит наличие экстремума функции в исследуемой точке.
определяется знаком второго дифференциала функции (если он не обращается в нуль). Следовательно от знака второго дифференциала зависит наличие экстремума функции в исследуемой точке. называется квадратичной формой, а квадратная матрица
называется квадратичной формой, а квадратная матрица 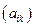 – матрицей квадратичной формы.
– матрицей квадратичной формы.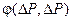 , матрица которой состоит из
, матрица которой состоит из 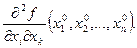 От свойств этой квадратичной формы и зависит имеет ли функция экстремум в рассматриваемой точке или нет.
От свойств этой квадратичной формы и зависит имеет ли функция экстремум в рассматриваемой точке или нет. называется положительно определённой, если она принимает положительные значения при всех значениях аргументов, не равных нулю одновременно.
называется положительно определённой, если она принимает положительные значения при всех значениях аргументов, не равных нулю одновременно. 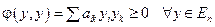 , причем
, причем  .
.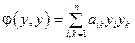 называется отрицательно определённой, если
называется отрицательно определённой, если 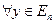
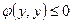
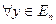


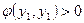 и
и 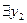
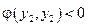 .
.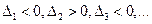
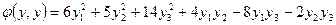 имеет матрицу:
имеет матрицу: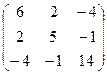 . Ее миноры:
. Ее миноры: 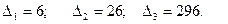
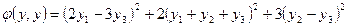 .
.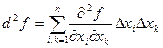 т.е. второй дифференциал функции,
т.е. второй дифференциал функции,
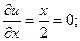
 .
.


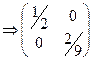 .
.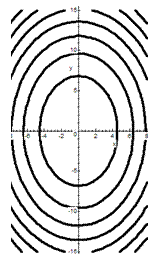 Главные миноры положительны, значит второй дифференциал положителен:
Главные миноры положительны, значит второй дифференциал положителен: 
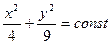 (эллипсы). Функция
(эллипсы). Функция  задает эллиптический параболоид.
задает эллиптический параболоид.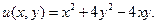
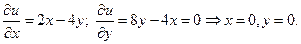
 Þ
Þ  . Второй дифференциал – полуопределён. Обратим внимание на то,что:
. Второй дифференциал – полуопределён. Обратим внимание на то,что:
 функция равна нулю, а вне этой линии u > 0. (параболический цилиндр).
функция равна нулю, а вне этой линии u > 0. (параболический цилиндр).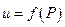 определена и непрерывна в ограниченной замкнутой области D. По теореме Вейерштрасса, функция в этой области достигает наибольшего и наименьшего значения.
определена и непрерывна в ограниченной замкнутой области D. По теореме Вейерштрасса, функция в этой области достигает наибольшего и наименьшего значения. в треугольнике:
в треугольнике: 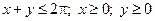 .
.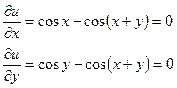 . Внутри области
. Внутри области 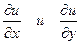 обращаются в ноль только в точке
обращаются в ноль только в точке  На границах области функция u = 0.
На границах области функция u = 0.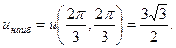
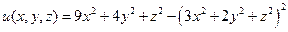 при условии
при условии 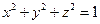 .
.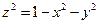 и, исключая из
и, исключая из 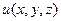 переменную
переменную  получим:
получим: . Сформулируем новую задачу:
. Сформулируем новую задачу: в круге x2 + y2
в круге x2 + y2  1.
1.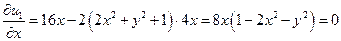 ;
; .
. ; (
; ( 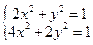 .
.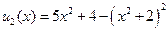 для
для 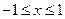 .
.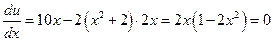 и, следовательно :
и, следовательно : = 0) б2). x =
= 0) б2). x =  = 1,
= 1,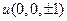 =
=  =
= 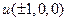 = 0.
= 0.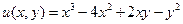 в прямоугольнике:
в прямоугольнике: 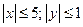 . Необходимые условия экстремума:
. Необходимые условия экстремума: 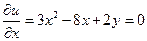 ,
,  .
.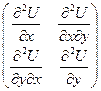 =
=  , D1 = – 8; D2 = 12.
, D1 = – 8; D2 = 12.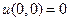 . Однако это значение не является наибольшим в области, ибо:
. Однако это значение не является наибольшим в области, ибо: 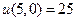 . ▲
. ▲