Полнота множеств логических связок и нормальные формы

Определение. Множество логических связок Q называется полным, если для каждого высказывания логики высказываний существует логически эквивалентное ему высказывание, содержащее только связки из Q.

Теорема. Множество {Ø, Ù, Ú} является полным.

Следствие. Для любого высказывания можно построить логически эквивалентное ему высказывание в дизъюнктивной или конъюнктивной нормальной форме (ДНФ или КНФ).

Дизъюнктивная нормальная форма. Пусть F — высказывание, содержащее атомы A₁, … , A_n. В общем случае ДНФ формулы F имеет вид

ДНФ(F): ,

где – атом или отрицание атома F, причем в конъюнктивную компоненту входит либо атом либо его отрицание.

Конъюнктивная нормальная форма формулы F

КНФ(F): ,

Таблицы истинности(Использование таблиц истинности для приведения высказывания к ДНФ или КНФ)

Пример. Привести к ДНФ (КНФ) следующее высказывание (A®B)®A

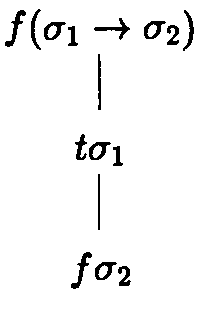
ДНФ(F) º t₁ Ú t₂ º (A Ù B) Ú (A Ù ØB)

КНФ(F) º f₃ Ù f₄ º (A Ú ØB) Ù (A Ú B)

Задание 2. Привести к ДНФ и КНФ следующие высказывания

1. (B®C)®((A®B)®(A®C))

2. (A®B)®((B®C)®(A®C))

3. (A®B) Ù (A Ù ØB)

Семантические таблицы Бета

Методы доказательства — это алгоритмические процедуры, следуя которым мы можем устанавливать, является ли высказывание тавтологией, и выполнимо ли множество высказываний. Эти методы разрабатываются в теории автоматического доказательства теорем и составляют основу логического программирования.

Первый из описанных методов алгоритмического доказательства использует семантические таблицы. Генцен в 1934 г. впервые доказал, что существует некоторая алгоритмическая процедура проверки тавтологичности формул. Бет и Хинтикка в 1955 г. построили алгоритм, устанавливающий, является высказывание тавтологией или нет.

При помощи семантических таблиц Бета можно исследовать возможность того, что данное высказывание принимает значение t или значение f.

Помеченные формулы и атомарные семантические таблицы

Пусть s - высказывание. Обозначим через fs утверждение «s ложно», а через ts — утверждение «s истинно». При этом fs и ts будем называть помеченными формулами.

Пусть А, s₁, s₂ – высказывания. Атомарными будем называть следующие семантические таблицы

tA	fA

В семантических таблицах ветвление обозначает дизъюнкцию, а последовательное соединение — конъюнкцию утверждений.

Построение семантической таблицы составного высказывания К начинается с того, что в корень семантической таблицы записывается помеченная формула tK или fK. Затем выполняется разворачивание семантической таблицы высказывания К с использованием атомарных формул.

Пример. Пусть К º (AÙØA)Ú(BÚ(CÙD)). Здесь A, B, C, D – атомы. Построим семантическую таблицу с корнем tK.

Вывод: Высказывание К выполнимо.

К является истинным (или гипотеза tK верна), если верна гипотеза tB или верны гипотезы tC и tD.

Основные понятия, необходимые для построения семантических таблиц

1. Вершинами семантической таблицы называются все помеченные формулы, встречающиеся в этой таблице.

2. Особые и обычные вершины.Вершина семантической таблицы называется особой, если она встречается как корень некоторой атомарной семантической таблицы. В противном случае, вершина называется обычной.

3. Противоречивая ветвь.Ветвь семантической таблицы называется противоречивой, если для некоторого высказывания s помеченные формулы ts и fs являются вершинами этой ветви.

4. Замкнутость таблицы.Семантическая таблица называется замкнутой, если каждая непротиворечивая ее ветвь не содержит обычных вершин. В противном случае, семантическая таблица называется незамкнутой.

5. Семантическая таблица противоречива, если каждая ее ветвь противоречива.

Не нашли, что искали? Воспользуйтесь поиском по сайту: