
|
|
Экстремум функции двух переменных12 Функция
Максимумы и минимумы функции называются экстремумами, а Необходимое условие экстремума: Если Точки, в которых частные производные первого порядка обращаются в ноль (или не существуют), называются критическими или стационарными. Исследование их на экстремум проводят с помощью достаточных условий существования экстремума функции двух переменных. Пусть 1) 2) 3) Условный экстремум Рассмотрим функцию Для отыскания условного экстремума исследуется на обычный экстремум функция Лагранжа Необходимые условия экстремума функции Лагранжа имеют вид:
Из этой системы Пример №21 Найти экстремумы функции Решение: Составляем функцию Лагранжа: Находим частные производные и составляем необходимые условия экстремума функции Лагранжа:
В данном случае Для исследования на экстремум в полученных критических точках вычисляем значения
Если Итак,
Задания:
а) b) c) 2. Найти условные экстремумы функций: а) b) c) Типовые примеры. Задание 1. Найти область определения функции z= Решение. Областью определения функции z= Найдём частные производные функции z. При нахождении z’x функция z дифференцируется по х, в предположении, что у=const. z’x= При нахождении z’y функция z дифференцируется по у, в предположении, что х=const z’y= Задание 2. Дана функция z=х Решение. Найдём частные производные функции z.
Подставим найденные производные в заданное выражение. Х x(у+е ху+хе 2ху+хе 2ху+хе Задание 3. Найти частные производные и частные дифференциалы функции z=ctg Решение. Найдём частные производные:
Найдём частные дифференциалы. dz dz
Задание 4. Вычислить значения частных производных f' f' f’ f’ f' f' f' Задание 5. Найти полный дифференциал функции z=ln(х cos 2y) Решение. Полный дифференциал функции определяется формулой dz= Найдём частные производные функции
Полный дифференциал dz= Задание 6. Вычислить значение производной сложной функции z= Решение. Производная сложной функции z=z(х;у), где х=х(t); у=у(t) может быть вычислена по формуле
Найдём все производные:
Тогда
Найдём значение производной
Задание7. Вычислить значения частных производных неявной функции е Решение. Если функция z задана неявно, т.е. в виде уравнения F(x;у;z)=0, то частные производные этой функции могут быть заданы по формулам:
Нам задана неявная функция е F Следовательно
Найдём производные в точке М
Задание 8.
S: z= Решение. Если уравнение поверхности задано в явной форме z=f(x,у), то уравнение касательной плоскости в точке М z- Уравнение нормали
Найдём частные производные данной функции и их значения в точке М f f Отсюда, применяя формулы, будем иметь z-1=2(x-2)+2(y+1) или 2х+2у-z-1=0 – уравнение касательной плоскости и
Решение. Если уравнение поверхности задано в неявной форме F (x,y,z)=0, то уравнение касательной плоскости и нормали будут иметь вид
Найдём частные производные функции F (x,y,z) и их значения в точке М
Следовательно уравнение касательной плоскости: -12(х-0)+0(у-2)-12(z+2)=0 или х+z+2=0 Уравнение нормали
Задание 9. Найти градиент функции Z= Решение. Градиентом функции z=f(x,y) называется вектор, проекциями которого на координатные оси являются соответствующие частные производные данной функции.
Найдём частные производные функции z и их значения в точке М
Следовательно, gradz=2 Задание 10. Исследовать на экстремум функцию z= Решение. Найдём частные производные:
Используя необходимое условие экстремума:
Составим систему уравнений
Решив эту систему найдём четыре стационарные точки.
Стационарные точки М Найдём производные второго порядка
И составим дискриминант ∆=А 1) Для точки М ∆=А В точке М 2) Для точки М ∆=144-36>0; А>0. В точке М 3) Для точки М ∆=36-144<0. Экстремума нет 4) Для точки М ∆=36-144<0. Экстремума нет Расчетные задания. Задание 1. Найти область определения указанных функций и частные производные.
3. z= 5. z= 7. z=arccos (x+y) 8. z= 9. z= 11. z= 13. z= 15. z= 17. z=arccos (x+2y) 18. z= arcsin (2x-y) 19. z= 21. z= 23. z= 25. z= 27. z= 29. z= Задание 2. 1. Дана функция z= 2. Дана функция z=х 3. Дана функция z=( 4. Дана функция z=arcsin 5. Дана функция z= 6. Дана функция z= 7. Дана функция 8. Дана функция z 9. Дана функция 10. Дана функция 11. Дана функция 12. Дана функция 13. Дана функция 14. Дана функция 15. Дана функция 16. Дана функция 17. Дана функция 18. Дана функция 19. Дана функция 20. Дана функция 21. Дана функция 22. Дана функция 23. Дана функция 24. Дана функция 25. Дана функция 26. Дана функция 27. Дана функция 28. Дана функция 29. Дана функция 30. Дана функция Задание 3. Найти частные производные и частные дифференциалы следующих функций
Задание 4. Вычислить значения частных производных f
30. Задание 5. Найти полные дифференциалы указанных функций 1.
Задание 6. Вычислить значение производной сложной функции z=z(х,у) где
Задание 7. Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
Задание 8. Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке
Задание 9. Найти градиент следующих функций в данной точке 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 имеет максимум ( минимум) в точке
имеет максимум ( минимум) в точке  если для любой точки
если для любой точки  , находящейся в некоторой
, находящейся в некоторой  - окрестности точки
- окрестности точки  , выполняется условие
, выполняется условие 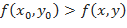
 ;
; , где
, где  – положительное достаточно малое число.
– положительное достаточно малое число. .
.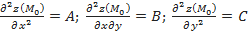 , а затем дискриминант
, а затем дискриминант  Тогда достаточные условия экстремума функции запишутся в следующем виде:
Тогда достаточные условия экстремума функции запишутся в следующем виде: – экстремум есть, при этом, если
– экстремум есть, при этом, если  ( или
( или 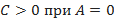 ), в точке
), в точке  ( или
( или  ) – максимум;
) – максимум; – экстремума нет;
– экстремума нет; – требуются дополнительные исследования.
– требуются дополнительные исследования. , определенную и дифференцируемую в области
, определенную и дифференцируемую в области  , координаты точек которой удовлетворяют системе уравнений связи
, координаты точек которой удовлетворяют системе уравнений связи  . В этой области нужно найти такую точку
. В этой области нужно найти такую точку  , чтобы выполнялось условие
, чтобы выполнялось условие  . Такие задачи называются задачами отыскания условного экстремума функции
. Такие задачи называются задачами отыскания условного экстремума функции 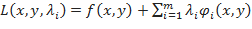 .
.
 уравнений с
уравнений с 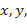
 . Числа
. Числа 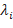 называются коэффициентами Лагранжа.
называются коэффициентами Лагранжа. при условии
при условии  .
.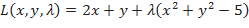 .
.

 .
.
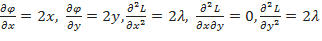 и составляем определитель:
и составляем определитель: .
. имеет в точке
имеет в точке  , следовательно, в точке
, следовательно, в точке  условный минимум,
условный минимум, 
 , следовательно, в точке
, следовательно, в точке  условный максимум,
условный максимум,  .
. ;
; ;
; .
.
 при
при 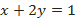 ;
;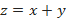 при
при 
 и её частные производные.
и её частные производные.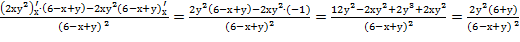

 у+х
у+х 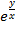 . Показать, что х
. Показать, что х 



 +у(х+е
+у(х+е 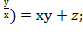

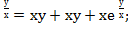
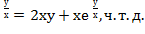
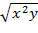

 ;
; =
= 

 f’
f’  , f’
, f’  в точке М
в точке М  (1;
(1;  для функции
для функции 
 =-
=- 
 ;
; ;
; ;
; (М
(М  ;
;

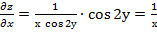

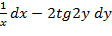
 , где х=е
, где х=е  ; у=2-е
; у=2-е  , при t
, при t 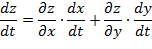



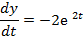

 в точке t
в точке t 
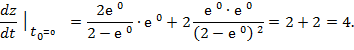
 в точке М
в точке М  ;
; 

 ;
;
 F
F  F
F 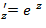


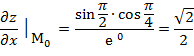

 в точке М
в точке М 
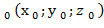 имеет вид
имеет вид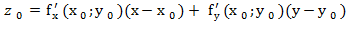 .
.

 (f
(f 
 (f
(f 
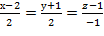 - уравнение нормали.
- уравнение нормали. в точке М
в точке М 
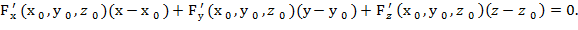

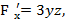




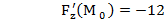
 или
или 
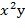 в точке М
в точке М 
 =
= 
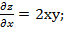



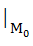 = 1
= 1







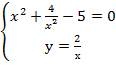
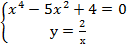

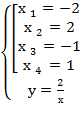
 (-2;-1); М
(-2;-1); М  (2;1); М
(2;1); М  (-1;-2); М
(-1;-2); М 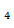 (1;2)
(1;2)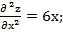
 =6у;
=6у; 
 для каждой стационарной точки
для каждой стационарной точки ; В=
; В= 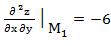 ; С=
; С= 
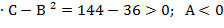 .
. =-8-6+30+12=28
=-8-6+30+12=28 =8+6-30-12=-28
=8+6-30-12=-28 2. z=arcsin (x-y)
2. z=arcsin (x-y) 4. z=
4. z= 
 6. z=
6. z= 

 10. z=
10. z= 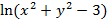
 12. z=
12. z= 
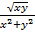 14. z=arcsin
14. z=arcsin 
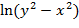 16. z=
16. z= 
 20. z=
20. z= 
 22. z=
22. z= 
 24. z=
24. z= 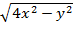
 26. z= arcsin (3x-y)
26. z= arcsin (3x-y) 28. z=
28. z= 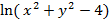
 30. z=
30. z= 
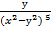 . Показать, что
. Показать, что  =
= 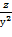
 . Показать, что
. Показать, что 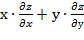 =z
=z tg
tg  . Показать, что
. Показать, что  . Показать, что
. Показать, что  . Показать, что
. Показать, что  . Показать, что
. Показать, что  =
= 
 Показать, что
Показать, что 
 . Показать, что
. Показать, что  =
= 
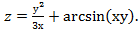 Показать, что
Показать, что  =0
=0 . Показать, что
. Показать, что 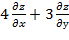 =0
=0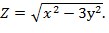 Показать, что 3у
Показать, что 3у  =0
=0 tg
tg 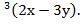 Показать, что 3у
Показать, что 3у 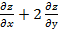 =0
=0 . Показать, что
. Показать, что  Показать, что
Показать, что 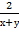
 Показать, что
Показать, что  =2
=2 . Показать, что
. Показать, что  =0
=0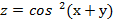 . Показать, что
. Показать, что  =0
=0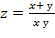 . Показать, что
. Показать, что  Показать, что
Показать, что  arc
arc 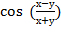 . Показать, что
. Показать, что 
 Показать, что
Показать, что  =0
=0 Показать, что
Показать, что  ). Показать, что
). Показать, что  . Показать, что
. Показать, что 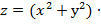 tg
tg  Показать, что
Показать, что 
 . Показать, что
. Показать, что 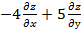 =0
=0 . Показать, что
. Показать, что  =0
=0 . Показать, что
. Показать, что  =0
=0 . Показать, что
. Показать, что 















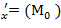 , f
, f  , f
, f  для данной функции f(х,у,z) в точке
для данной функции f(х,у,z) в точке 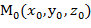


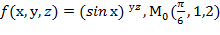

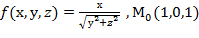







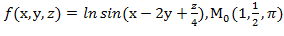




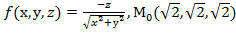




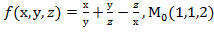
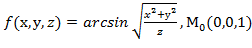


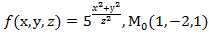
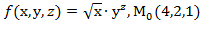
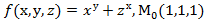
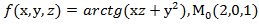

























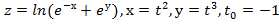



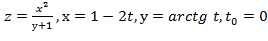


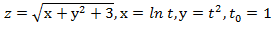
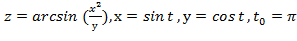









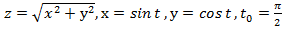


 =4
=4 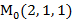
 =2
=2 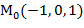

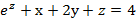

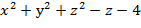 =0
=0 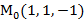
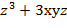 +3у=7
+3у=7 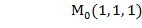
 х+
х+ 

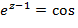 х
х  у+1
у+1 
 =0
=0 


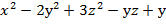 =2
=2 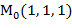
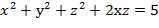
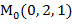
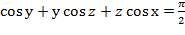
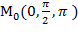













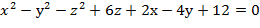
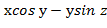 =
= 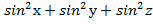 =
= 





 +
+  =2
=2 
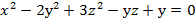

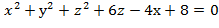


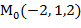



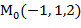




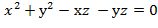
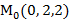
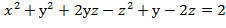

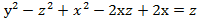

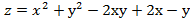



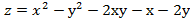





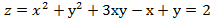




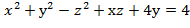







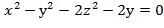




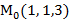








 )
)