
|
|
Предел и непрерывность функции.12 Дифференциальное исчисление функции одной переменнойи нескольких переменных Методические указания и задания Для выполнения типового расчета По курсу «Математика» Направление подготовки
Продукты питания из растительного сырья Саратов 2013 Дифференциальное исчисление функции одной переменной:метод. указания и задания для выполнениятипового расчета по курсу «Математика» для направления подготовки 260100.62 Продукты питания из растительного сырья / сост. Н.В. Дьяконова //ФГБОУ ВПО «Саратовский ГАУ».- Саратов, 2013.- Методические указания и задания для выполнения типового расчета по дисциплине «Математика» составлены в соответствии с программой и предназначены для студентов направления подготовки 260100.62 Продукты питания из растительного сырья, 221400.62 Управление качеством. Они содержат рекомендации, примеры и задания к выполнению типового расчета. Позволяют студентам освоить основные математические методы, необходимые для анализа процессов и явлений в ходе поиска оптимальных решений практических задач, обучает методам обработки и анализа результатов эксперимента. Курс нацелен на формирование ключевых компетенций, необходимых для эффективного решения профессиональных задач и организации профессиональной деятельности.
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ 1. Работа выполняется на листах формата А4 (210х297), которые затем скрепляются. 2. Решение заданий следует сопровождать краткими пояснениями. 3. Исходные данные для заданий типового расчета представлены в таблицах. Из таблицы каждый студент выбирает строки с номерами вариант, которые соответствуют номеру в списке группового журнала.
Определение 4.1. Если каждому значению переменной Переменная Определение 4.2. Совокупность значений Пример1: Функция Определение 4.3.Если функция Основными способами задания функции являются: табличный, графический, аналитический. К основным элементарным функциям относят следующие, аналитическим способом заданные функции:
Определение 4.4. Функция Наименьшее такое число называется периодом функции. Пример №2. Найти область определения функции Решение: Областью определения функции является отрезок Задания: Найти область определения функции: 1) 2) 3) 4)
Предел и непрерывность функции. Определение 4.5. Пусть функция Определение 4.6. Функция
Определение 4.7. Если функция Свойства пределов. Теорема 1:Предел алгебраической суммы двух, трёх и вообще определённого числа переменных равен алгебраической сумме пределов этих переменных:
Пример №3 Теорема 2: Предел произведения двух, трёх или вообще определённого числа переменных равен произведению пределов этих переменных Пример №4 Теорема 3: Предел частного двух переменных равен частному пределов этих переменных, если предел знаменателя отличен от нуля: Пример №5 Пример №6Найти Здесь знаменатель и числитель при
Первый замечательный предел:
Второй замечательный предел:
Задания: Вычислить указанные пределы: 1) 2) 3) 4) 5) 6) 7) 8) 9) 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , при надлежащему некоторой области, соответствует одно определённое значении другой переменной
, при надлежащему некоторой области, соответствует одно определённое значении другой переменной  , то
, то  ,
,  .
.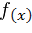 называется областью определения функции ( или областью существования функции ).
называется областью определения функции ( или областью существования функции ).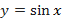 определена при всех значениях
определена при всех значениях 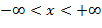 .
. , где
, где  - действительное число;
- действительное число;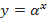 , где
, где  , где
, где  ,
, 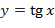 ,
, 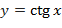 ,
,  ,
,  .
.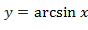 ,
,  ,
,  ,
,  ,
, 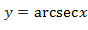 ,
,  .
. .
. .
. , т.к.
, т.к. 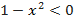 при
при  , следовательно, функция
, следовательно, функция  не определена при этих значениях
не определена при этих значениях  ( Ответ:
( Ответ:  );
); ( Ответ:
( Ответ:  );
);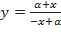 ( Ответ:
( Ответ: 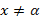 );
); при
при 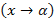 , если для каждого положительного числа
, если для каждого положительного числа  , как бы мало оно ни было, можно указать такое положительное число
, как бы мало оно ни было, можно указать такое положительное число  , что для всех
, что для всех  имеет место неравенство
имеет место неравенство  . Если
. Если 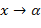 , то пишут:
, то пишут:  .
. ( или в точке
( или в точке  ), если она определена в некоторой окрестности точки
), если она определена в некоторой окрестности точки 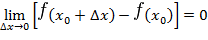
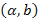 , где
, где 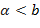 , то говорят, что функция непрерывна на этом интервале.
, то говорят, что функция непрерывна на этом интервале.

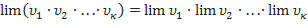
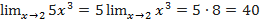 .
.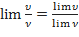 .
.

 стремится к нулю, и, следовательно, теорема 3 неприменима. Произведём следующее тождественное преобразование:
стремится к нулю, и, следовательно, теорема 3 неприменима. Произведём следующее тождественное преобразование: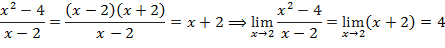
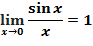

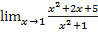 ;
; ;
; ;
;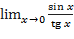 ;
;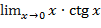 ;
; ;
;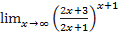 ;
; ;
;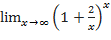 .
.