|
|
Решение задачи 2 (алгоритм обратной прогонки)12 В предыдущем решении задачи 2 вычисления проводились последовательно: от первого этапа до третьего. Такая последовательность вычислений известна как алгоритм прямой прогонки. Этот же пример может быть решен с помощью алгоритма обратной прогонки, в соответствии с которым вычисления проводятся от третьего этапа до первого. Алгоритмы прямой и обратной прогонки приводят к одному и тому же решению. Несмотря на то, что алгоритм прямой прогонки представляется более логичным, в специальной литературе, посвященной динамическому программированию, неизменно используется алгоритм обратной прогонки. Причина этого в том, что в общем случае алгоритм обратной прогонки может быть более эффективным с вычислительной точки зрения. Рекуррентное уравнение для алгоритма обратной прогонки в задаче 2 имеет вид:
где Этап 3.Так как узел 7 (
Этап 2.Так как маршрута (2,6) не существует, соответствующая альтернатива не рассматривается. Используя значения
Оптимальное решение второго этапа означает следующее. Если вы находитесь в узле (городе) 2 или 4, кратчайший путь к узлу 7 проходит через узел 5, а если находитесь в узле 3, кратчайший путь к узлу 7 проходит через узел 6. Этап I.Из узла 1 имеем три альтернативных маршрута: (1,2), (1,3) и (1,4). Используя значения
Оптимальное решение на первом этапе показывает, что кратчайший путь проходит через город 4. Далее из оптимального решения на втором этапе следует, что из города 4 необходимо двигаться в город 5. Наконец, из оптимального решения на третьем этапе следует, что город 5 связан с городом 7. Следовательно, полным маршрутом, имеющим кратчайшую длину, является 1-4-5-7, и его длина равна 21 км. Пример задачи 3 «замена оборудования» Компания планирует оптимальную политику замены имеющегося в настоящее время трехлетнего механизма на протяжении следующих 4 лет (n=4), т.е. вплоть до начала пятого года. Приведенная таблица содержит относящиеся к задаче данные. Компания требует замены механизма, который в эксплуатации 6 лет. Стоимость нового механизма равна 100 000 долл.
Решение задачи 3 Определение допустимых значений возраста механизма на каждом этапе является нетривиальной задачей. На рис. 10.4 представлена рассматриваемая задача замены оборудования в виде сети. В начале первого года имеется механизм трехлетнего возраста. Можем либо заменить его (3), либо эксплуатировать (С) на протяжении следующего года. Если механизм заменили, то в начале второго года его возраст будет равен одному году, в противном случае его возраст будет 4 года. Такой же подход используется в начале каждого года, начиная со второго по четвертый. Если однолетний механизм заменяется в начале второго или третьего года, то заменивший его механизм к началу следующего года также будет однолетним. К тому же, в начале 4-го года 6-летний механизм обязательно должен быть заменен, если он еще эксплуатируется; в конце 4-го года все механизмы продаются (П) в обязательном порядке. На схеме сети также видно, что в начале второго года возможны только механизмы со сроком эксплуатации 1 или 4 года. В начале третьего года механизм может иметь возраст 1, 2 или 5 лет, а в начале четвертого — 1,2,3 или 6 лет.
Рисунок 10.4 – Маршруты Решение данной задачи эквивалентно нахождению маршрута максимальной длины (т.е. приносящего максимальную прибыль) от начала первого года к концу четвертого в сети. При решении этой задачи используем табличную форму записи (числовые данные в таблице кратны тыс. долл.).
В начале первого года оптимальным решением при t = 3 является замена механизма. Следовательно, новый механизм к началу второго года будет находиться в эксплуатации 1 год. При t = 1 в начале второго года оптимальным решением будет либо использование, либо замена механизма. Если он заменяется, то новый к началу третьего года будет находиться в эксплуатации 1 год, иначе механизм будет иметь возраст 2 года. Описанный процесс продолжается до тех пор, пока не будет определено оптимальное решение для четвертого года (рис. 10.5).
Рисунок 10.5 – Последовательность получения оптимального решения Следовательно, начиная с первого года эксплуатации механизма, альтернативными оптимальными стратегиями относительно замены механизма будут (3, С, С, 3) и (3, 3, С, С). Общая прибыль составит 55 300 долларов.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 для
для  . Соответствующей последовательностью вычислений будет
. Соответствующей последовательностью вычислений будет 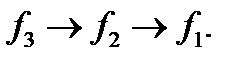
 = 7) связан с узлами 5 и 6 (х3 = 5 и 6) в точности одним маршрутом, альтернативы для выбора отсутствуют, а результаты третьего этапа можно подытожить следующим образом.
= 7) связан с узлами 5 и 6 (х3 = 5 и 6) в точности одним маршрутом, альтернативы для выбора отсутствуют, а результаты третьего этапа можно подытожить следующим образом.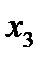



 +
+ 


 +
+ 

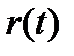 +s(t+1)-
+s(t+1)- 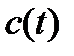
 +s(t)+s(1)-
+s(t)+s(1)-  -I
-I


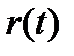 -
-