
|
|
Решение задачи 2 (алгоритм прямой прогонки)12 Тема 10. Динамическое программирование: задача о кратчайшем пути Цель: решение задачи о кратчайшем пути и задачи замены оборудования методами динамического программирования. Пример задачи 1 «о кратчайшем пути» Дана схема маршрута движения (рисунок 10.1) с указанными на ней длинами lij маршрутов (км). Определить кратчайший маршрут движения из пункта А в В (где i – исходный пункт, j - входящий).
Рисунок 10.1 – Метки на маршрутах Решение задачи 1 1. Определим шаги оптимизации: их всего четыре. 2. Присваиваем функцию длины маршрута на последнем шаге F4 = 0 и далее по шагам до начального (нулевого) шага: Шаг 3. F3 = l3,4 + F4 = 8 + 0 = 8. Шаг 2. На этом шаге два пункта (2/1) и (2/2).
F2,2 = l2 / 2,4 + F4 = 5 + 0 = 5. Шаг 1. На этом шаге также два пункта:
Шаг 0. Начало движения: 3. По выделенным на каждом шаге маршрутам (подчеркнуты линией) формируем кратчайший, составляющий целевую функцию F0 = 24. Пример задачи 2 «о кратчайшем пути» Для доставки продукции необходимо выбрать кратчайший путь между двумя городами. Сеть дорог, показанная на рис. 10.2, представляет возможные маршруты между исходным городом, находящимся в узле 1, и конечным пунктом в узле 7. Маршруты проходят через промежуточные города, обозначенные на сети узлами с номерами 2-6.
Рисунок 10.2 – Метки на маршрутах Решение задачи 2 (алгоритм прямой прогонки) Можно решить эту задачу посредством полного перебора всех маршрутов между узлами 1 и 7 (имеется пять таких маршрутов). Однако в большой сети полный перебор является неэффективным с вычислительной точки зрения. Чтобы решить эту задачу с помощью методов динамического программирования, сначала разделим ее на этапы. Вертикальные пунктирные линии на рис. 10.3 очерчивают три этапа задачи. Далее выполняются вычисления для каждого этапа в отдельности.
Рисунок 10.3 – Этапы задачи Общая задача состоит в вычислении кратчайших (постепенно накапливаемых) расстояний ко всем вершинам этапа с последующим использованием этих расстояний в качестве исходных данных для следующего этапа. Рассматривая узлы, относящиеся к первому этапу, замечаем, что каждый из узлов 2, 3 и 4 связан с начальным узлом 1 единственной дугой. Следовательно, для первого этапа имеем следующее. Этап 1.Кратчайший путь к узлу 2 равен 7 км (из узла 1), Кратчайший путь к узлу 3 равен 8 км (из узла 1), Кратчайший путь к узлу 4 равен 5 км (из узла 1). Далее переходим ко второму этапу для вычисления кратчайших (накопленных) расстояний к узлам 5 и 6. Рассматривая узел 5 первым, из рис. 10.2 замечаем, что есть три возможных маршрута, по которым можно достичь узла 5, а именно (2, 5), [ (3, 5) и (4, 5). Эта информация вместе с кратчайшими расстояниями к узлам 2, 3, и 4 определяет кратчайшее (накопленное) расстояние к узлу 5 следующим образом.
Аналогично для узла 6 имеем следующее.
Этап 2.Кратчайший путь к узлу 5 равен 12 км (из узла 4), Кратчайший путь к узлу 6 равен 17 км (из узла 3). Последним шагом является третий этап. Конечный узел 7 можно достигнуть как из узла 5, так и 6. Используя итоговые результаты этапа 2 и расстояния от узлов 5 и 6 к узлу 7, получаем следующее:
Этап 3.Кратчайший путь к узлу 7 равен 21 км (из узла 5). Приведенные вычисления показывают, что кратчайшее расстояние между узлами 1 и 7 равно 21 км. Города, через которые проходит кратчайший маршрут, определяется следующим образом. Из готовых результатов третьего этапа следует, что узел 7 связывается с узлом 5. Далее из итоговых результатов второго этапа следует, что узел 4 связывается с узлом 5. Наконец, из готовых результатов первого этапа следует, что узел 4 связывается с узлом 1. Следовательно, оптимальным маршрутом является последовательность 1-4-5-7. Теперь покажем, как рекуррентные вычисления динамического программирования можно выразить математически. Пусть
При i=1 полагаем Определение состояниясистемы приводит к следующему унифицированному положению. Принцип оптимальности:на каждом этапе оптимальная стратегия определяется независимо от стратегий, примененных на предыдущих этапах. Применение принципа оптимальности демонстрируется вычислениями для задачи 2. Например, на этапе 3 используем кратчайшие пути к узлам 5 и 6 и не интересуемся, как эти узлы были достигнуты из узла 1.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|







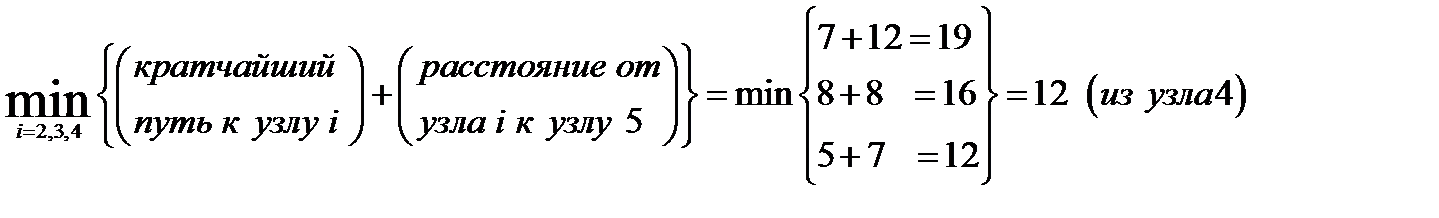



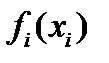 – кратчайшее расстояние до вершины
– кратчайшее расстояние до вершины  на этапе
на этапе  – расстояние от узла
– расстояние от узла  до узла
до узла  вычисляется из
вычисляется из 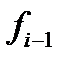 с помощью следующего рекуррентного уравнения:
с помощью следующего рекуррентного уравнения:
 . Это уравнение показывает, что кратчайшие расстояния
. Это уравнение показывает, что кратчайшие расстояния  . В действительности состояниесистемы на этапе i — это информация, связывающая этапы между собой, при этом оптимальные решения для оставшихся этапов могут приниматься без повторной проверки того, как были получены решения на предыдущих этапах. Такое определение состояниясистемы позволяет рассматривать каждый этап отдельно и гарантирует, что решение является допустимым на каждом этапе.
. В действительности состояниесистемы на этапе i — это информация, связывающая этапы между собой, при этом оптимальные решения для оставшихся этапов могут приниматься без повторной проверки того, как были получены решения на предыдущих этапах. Такое определение состояниясистемы позволяет рассматривать каждый этап отдельно и гарантирует, что решение является допустимым на каждом этапе.