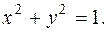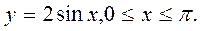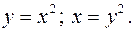|
|
Интегрирование тригонометрических функцийРассмотрим интеграл типа Действительно, Тогда, подставляя в данный интеграл вместо Пример13. Вычислить интеграл Решение. Подстановка
Универсальная подстановка нередко приводит к сложным вычислениям. Поэтому в указанных ниже случаях предпочтительней частные подстановки, также рационализирующие интеграл. если если если Пример14. Вычислить интеграл Решение. Положим
Рассмотрим интеграл вида 1. Одно из чисел m или n – нечетное, например
2. Оба числа m и n – четные. Тогда рекомендуется воспользоваться тригонометрическими формулами понижения степени:
Пример15. Вычислить интеграл Решение. Интегрирование некоторых иррациональных функций Рассмотрим интеграл следующего вида: где R - рациональная функция, Пример16. Вычислить интеграл Решение. Положив Контрольные задания Вычислить неопределенные интегралы. 5.1 5.2 5. 5. 5. 5. 5. 5. 5. 5. 5. 5.12 5.13
5.14
5.15
5.16
5.17
5.18
5.19
5.20
Указания к заданию 6. Пусть функция В каждом из полученных частичных промежутков Пусть Функция Выясним геометрический смысл суммы Римана
Рис.5
Таким образом, Свойства определенного интеграла Пусть все рассматриваемые функции являются непрерывными, так что определенные интегралы от них существуют. Тогда справедливы следующие соотношения: 1. 2. 3. 4. 5. 6. Если Если функции
Правую часть формулы часто обозначают символом Пример1. Вычислить определенный интеграл Решение.
Замена переменной в определенном интеграле Пусть функция Тогда:
Эта формула называется формулой замены переменной в определенном интеграле или формулой интегрирования подстановкой. Пример2. Вычислить определенный интеграл Решение. Сделаем замену переменной Тогда
Заметим, что при вычислении определенного интеграла к старой переменной не возвращаются.
Интегрирование по частям в определенном интеграле Теорема. Если функции Пример3. Вычислить Решение. Обозначим Тогда
Геометрические приложения определенного интеграла Площадь плоской фигуры Площадь Если часть кривой
Пусть фигура ограничена двумя кривыми
Рис.6
Рис. 7
Рис. 8
Пример 4. Вычислить площадь фигуры, ограниченной прямой Решение. Построим графики прямой и параболы (рис. 9).
Рис. 9
Найдем точки пересечения параболы и прямой:
Тогда получим:
Объем тела вращения Пусть функция
Если тело получено вращением кривой
Пример5. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями Решение. На рис.10 показана фигура, образующая тело вращения.
Рис. 10
Контрольные задания Вычислить площадь фигуры, ограниченной линиями (6.1-6.20) . Вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций, вокруг оси OX (6.1.1-6.1.20). Вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций вокруг оси OY (6.2.1-6.2.20). 6.1. 6.2. 6.3. 6.4. 6.5. 6.6. 6.7. 6.8. 6.9. 6.10. 6.11. 6.12. 6.13. 6.14. 6.15. 6.16. 6.17. 6.18. 6.19. 6.20.
6.1.1. 6.1.2. 6.1.3. 6.1.4. 6.1.5. 6.1.6. 6.1.7. 6.1.8. 6.1.9. 6.1.10. 6.1.11. 6.1.12. 6.1.13. 6.1.14. 6.1.15. 6.1.16. 6.1.17. 6.1.18. 6.1.19. 6.1.20.
6.2.1. 6.2.2. 6.2.3. 6.2.4. 6.2.5. 6.2.6. 6.2.7. 6.2.8. 6.2.9. 6.2.10. 6.2.11. 6.2.12. 6.2.13. 6.2.14. 6.2.15. 6.2.16. 6.2.17. 6.2.18. 6.2.19. 6.2.20. Требования к выполнению контрольной работы
К оформлению работ предъявляются следующие требования: 1. Работа выполняется в тетради со свободными полями для замечаний рецензента. 2. На обложке тетради должны быть указаны фамилия и инициалы студента, номер зачетной книжки, шифр, номер специальности, срок обучения, название дисциплины. 3. Контрольная работа должна содержать все задачи своего варианта, расположенные в порядке, указанном в задании. Перед решением каждой задачи должны приводиться ее условия. 4. Решение следует излагать подробно и аккуратно, делая необходимые объяснения и иллюстрации. 5. В случае получения от рецензента незачтенной работы следует исправить все отмеченные ошибки, внести необходимые исправления и прислать работу для повторной проверки. Рекомендуется при выполнении работы оставлять в конце тетради несколько чистых листов для внесения возможных исправлений после ее рецензирования. Варианты контрольных заданий приведены в конце каждого из разделов, раскрывающих каждую из перечисленных тем. Список литературы
1. Грес П.В. Математика для гуманитариев: Учебное пособие.- М.: Логос, 2006. 2. ДАНКО П.Е., ПОПОВ А.Г., КОЖЕВНИКОВА Т.Я. Высшая математика в упражнениях и задачах. М.: Высшая школа, 2006. 3. ЕРМАКОВ В.И. Сборник задач по высшей математике для экономистов: учебное пособие. М.:Инфра-М, 2005. 4. Красс М.С. Математика для экономистов: Учебное пособие/ М.С.Красс, Б.П.Чурынов.- СПб: Питер, 2004. 5. КРЕМЕР Н.Ш., ПУТКО Б.А., ТРИШИН Н.М., ФРИДМАН Н.М. Высшая математика для экономистов. М.: Банки и биржи, ЮНИТИ, 2008. ШИПАЧЕВ В.С. Высшая математика. М.: Высшая школа, 2005. Приложение 1 Содержание дисциплины (извлечение из рабочей программы дисциплины) РАЗДЕЛ 1. АЛГЕБРА И ГЕОМЕТРИЯ. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Тема 1.1. Элементы линейной алгебры. Алгебраические структуры. Матрицы и действия с ними. Определители и их свойства Обратная матрицы Теорема Крамера. Системы линейных алгебраических уравнений. Ранг матрицы. Теорема Кронекера-Капелли. Метод Гаусса-Жордана. Линейная балансовая модель. Тема 1.2. Аналитическая геометрия и линейная алгебра. Прямоугольная система координат в пространстве. Понятие вектора. Линейные операции над векторами. Теоремы о проекциях векторов. Векторные пространства. Линейные отображения. Линейная зависимость векторов. Скалярное, векторное, смешанное произведения векторов и выражение их через координаты. Векторное параметрическое уравнение прямой. Бюджетная линия и многотоварное бюджетное уравнение. Задача о делении отрезка в заданном отношении. Координатные уравнения прямой в пространстве. Координатные уравнения прямой на плоскости. Нормированное уравнение прямой. Угол между двумя прямыми на плоскости. Взаимное расположение прямых на плоскости. Координатное уравнение плоскости. Общие уравнения прямой в пространстве. Взаимное расположение прямых и плоскостей в пространстве. Некоторые приложения к экономике. Линии второго порядка. Многомерная геометрия кривых и поверхностей. Тема 1.3. Введение в анализ функций одной переменной. Множества. Грани числовых множеств. Абсолютная величина числа. Понятие функции. Классификация функций. Предел последовательности. Теоремы о сходящихся последовательностях. Действия с пределами. Бесконечно малые и бесконечно большие последовательности. Теоремы о сумме (разности), произведении и частном сходящихся последовательностей. Предельный переход в неравенствах. Монотонные последовательности. Число ℮. Предел функции в точке, Теоремы о пределах функции. Первый и второй замечательные пределы. Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых функций. Асимптотические формулы. Непрерывность функции в точке. Классификация точек разрыва. Основные свойства непрерывных функций. Понятие сложной и обратной функций. Тема 1.4. Дифференциальное исчисление функции одной переменной. Понятие производной, ее геометрический, механический и экономический смысл. Понятие дифференцируемости функции. Связь между понятиями дифференцируемости и непрерывности. Понятие дифференциала. Правила дифференцирования. Производная постоянной функции. Производные тригонометрических функций. Производная логарифмической функции. Производная обратной функции. Производная сложной функции. Вычисление производных показательных и обратных тригонометрических функций. Логарифмическая производная. Производная степенной функции. Таблица простейших элементарных функций. Дифференцирование функции заданной параметрически. Некоторые приложения к экономике. Теоремы Ферма, Ролля, Лагранжа, Коши и их геометрический смысл. Теорема Лопиталя. Теорема Тейлора. Признак монотонности. Необходимые и достаточные условия локального экстремума. Направления выпуклости и точки перегиба графика функции. Необходимое и достаточное условия точки перегиба. Асимптоты графика функции. Схема исследования функции и построения графика. РАЗДЕЛ 2. МАТЕМАТИЧЕСКИЙ АНАЛИЗ:ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ. Тема 2.1. Неопределенный интеграл. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла. Таблица основных интегралов. Непосредственное интегрирование. Метод подстановки. Метод интегрирования по частям. Интегрирование рациональных функций. Интегрирование некоторых иррациональных функций. Универсальная тригонометрическая подстановка. Частные тригонометрические подстановки. Вычисление интегралов от четных и нечетных степеней синуса и косинуса. Интегрирование иррациональностей с помощью тригонометрических подстановок.
Тема 2.2. Определенный интеграл. Понятие определенного интеграла, суммы Дарбу. Необходимое и достаточное условие интегрируемости. Некоторые классы интегрируемых функций. Свойства определенного интеграла. Теорема о среднем. Интеграл с переменным верхним пределом. Формула Ньютона- Лейбница. Замена переменной в определенном интеграле. Формула интегрирования по частям в определенном интеграле. Некоторые приложения определенного интеграла. Несобственные интегралы первого и второго родов. Формулы прямоугольников, трапеций, Симпсона (парабол). Тема 2.3. Функции нескольких переменных. Понятие функции нескольких переменных. Непрерывность функции нескольких переменных. Частные производные. Определение дифференцируемости. Дифференциал функции нескольких переменных и его геометрический смысл. Производная сложной функции. Векторный анализ элементы теории поля. Скалярное поле Производная по направлению. Градиент. Векторное поле. Экстремумы функций. Необходимое условие экстремума. Достаточное условие экстремума. Метод наименьших квадратов. Формула Тейлора. Вогнутые функции.
Тема 2.4. Двойной интеграл. Двойные интегралы. Определение и условие существования. Геометрический смысл двойного интеграла. Свойства двойного интеграла. Сведение двойного интеграла к повторному. Замена переменных в двойном интеграле. Интегрирование по неограниченным областям. Интеграл Эйлера-Пуассона. Некоторые приложения двойных интегралов. Приложение 2
Образец оформления титульного листа Контрольной работы Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный экономический университет»
Кафедра высшей математики
Контрольная работа по дисциплине
МАТЕМАТИКА Выполнил: __________ (Фамилия И.О.)________________
студент ____ курса (срок обучения) спец. _____________ группа______№ зачет. книжки ________________________
Подпись: ___________________________________________
Преподаватель: __________ (Фамилия И.О.) _____________
Должность: ___________(уч. степень, уч. звание) __________
Оценка: ______________ Дата: ________________________
Подпись: _____________________________________________ 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
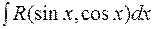 , где R обозначает рациональную функцию своих аргументов
, где R обозначает рациональную функцию своих аргументов 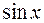 и
и  . Интеграл данного типа сводится к интегралу от рациональной функции с помощью, так называемой универсальной постановки
. Интеграл данного типа сводится к интегралу от рациональной функции с помощью, так называемой универсальной постановки  .
.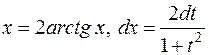 и
и 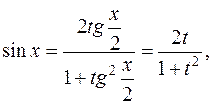
 =
= 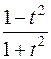 .
.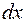 полученные выражения, будем иметь под знаком интеграла рациональную функцию.
полученные выражения, будем иметь под знаком интеграла рациональную функцию.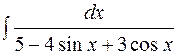 .
.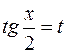 дает:
дает:
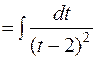 =
= 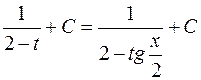 .
. , то применима подстановка
, то применима подстановка 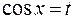 ;
;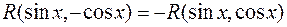 , то применима подстановка
, то применима подстановка 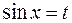 ;
; , то применима подстановка
, то применима подстановка 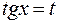 .
. .
. поэтому:
поэтому: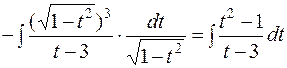 =
= 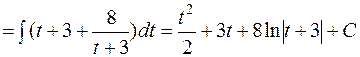 =
=  .
.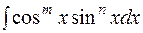 , где m и n-целые числа. Возможны следующие случаи:
, где m и n-целые числа. Возможны следующие случаи: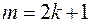 , тогда полагая
, тогда полагая 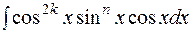 =
= 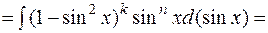


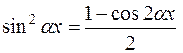 .
.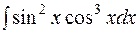 .
.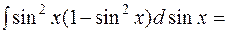
 =
=  .
.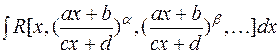 ,
,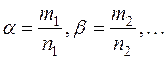 - рациональные числа. Данный интеграл сводится к интегралу от рациональной функции с помощью подстановки
- рациональные числа. Данный интеграл сводится к интегралу от рациональной функции с помощью подстановки  , где k - общий знаменатель всех дробных показателей.
, где k - общий знаменатель всех дробных показателей. .
.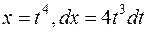 , получим:
, получим: 

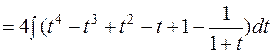 =
= 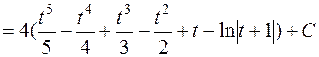 =
= 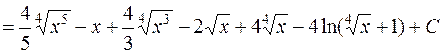 .
.
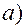
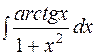
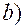
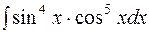
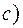
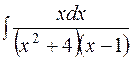
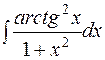
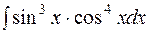
 .
.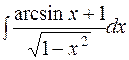
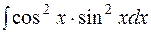
 .
.
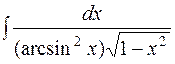
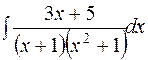 .
.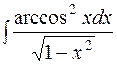

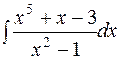 .
.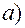
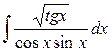
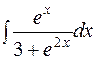
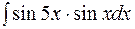 .
.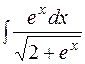

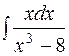 .
.

 .
.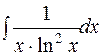
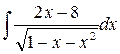
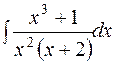 .
.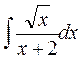

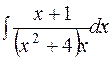

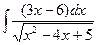
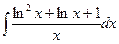 .
.

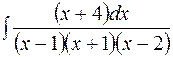 .
.
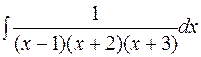
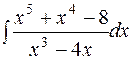 .
.

 .
.

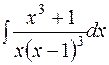 .
.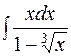

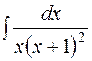 .
.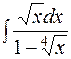
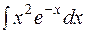
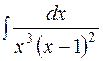 .
.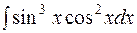
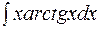
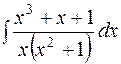 .
.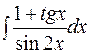
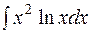
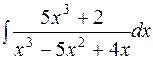 .
.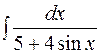

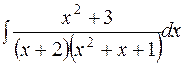 .
.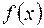 определена на отрезке
определена на отрезке 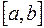 . Разобьем этот промежуток произвольным образом на n частей точками
. Разобьем этот промежуток произвольным образом на n частей точками  .
.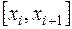 , где
, где 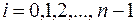 , выберем произвольную точку
, выберем произвольную точку  . Вычислим значение функции
. Вычислим значение функции  и умножим его на разность
и умножим его на разность 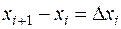 , после этого составим сумму
, после этого составим сумму 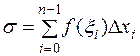 , которая называется интегральной суммой Римана для функции
, которая называется интегральной суммой Римана для функции 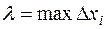 , т.е. длина наибольшего частичного промежутка. Если существует конечный предел интегральной суммы
, т.е. длина наибольшего частичного промежутка. Если существует конечный предел интегральной суммы 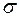 при
при 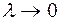 , не зависящий ни от способа разбиения промежутка
, не зависящий ни от способа разбиения промежутка  , то этот предел называется определенным интегралом функции
, то этот предел называется определенным интегралом функции  . Таким образом,
. Таким образом, 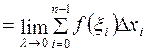 .
.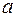 и
и 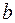 называются соответственно нижним и верхним пределами интеграла.
называются соответственно нижним и верхним пределами интеграла.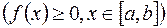 . В этом случае произведение
. В этом случае произведение 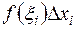 равно площади прямоугольника с основанием
равно площади прямоугольника с основанием 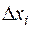 и высотой
и высотой 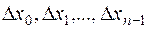 и высотами
и высотами 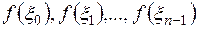 (рис. 5).
(рис. 5).


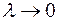 , т.е. площади криволинейной трапеции, ограниченной графиком функции
, т.е. площади криволинейной трапеции, ограниченной графиком функции 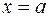 и
и 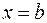 и отрезком
и отрезком  .
.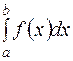
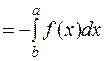
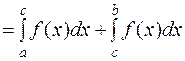
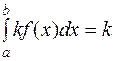

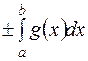

 .
.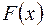 - какая-нибудь первообразная для
- какая-нибудь первообразная для  .
.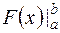 (знак двойной подстановки от
(знак двойной подстановки от  .
.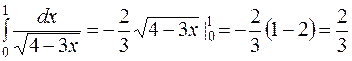 .
.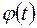 определена и непрерывна вместе со своей производной
определена и непрерывна вместе со своей производной  на отрезке
на отрезке 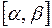 , причем
, причем 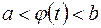 для любого
для любого 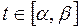 и
и 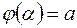 ,
, 
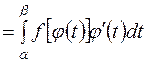
 .
.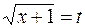 .
.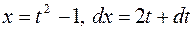 . Пересчитаем пределы интегрирования: при
. Пересчитаем пределы интегрирования: при 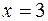
 , а при
, а при 
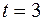 .
.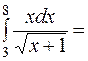
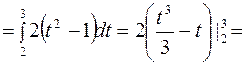
 .
. и
и 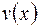 дифференцируемы на отрезке
дифференцируемы на отрезке 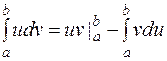 .
.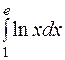 .
.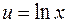 ,
,  .
. ,
, 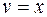 .
.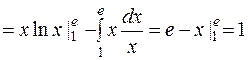 .
. криволинейной трапеции, ограниченной графиком
криволинейной трапеции, ограниченной графиком  , осью
, осью 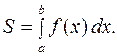
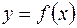 находится под осью
находится под осью  .
.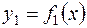 ,
, и
и  ,
, 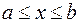 (рис. 8). Тогда ее площадь вычисляется по формуле
(рис. 8). Тогда ее площадь вычисляется по формуле 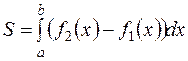 .
.
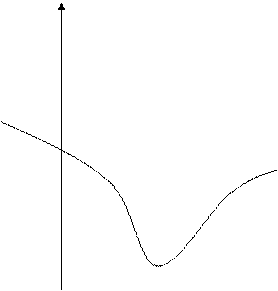
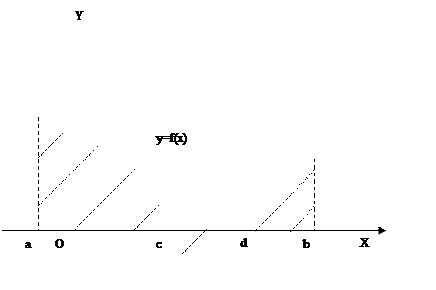

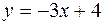 и параболой
и параболой  .
.

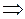
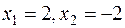 .
.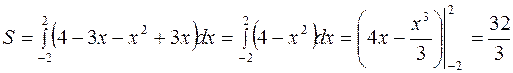 .
.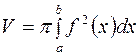 .
.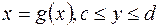 вокруг оси
вокруг оси 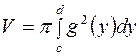 .
.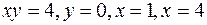 вокруг оси
вокруг оси 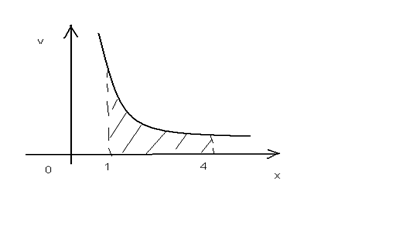
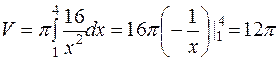 .
.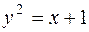 ;
; 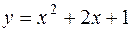 .
.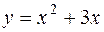 ;
; 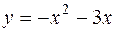 .
.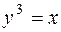 ;
; 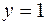 ;
;  ;
; 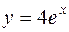 ;
;  ;
;  .
.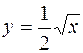 ;
;  ;
; 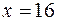 .
.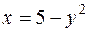 ;
; 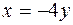 .
.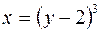 ;
;  .
.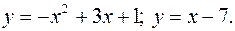
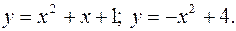
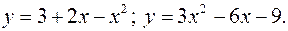
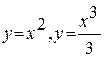 .
.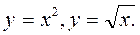 .
.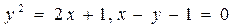 .
. .
. .
.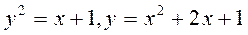 .
.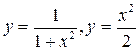 .
.

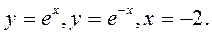
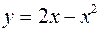 ;
; 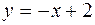 .
. ;
;  .
.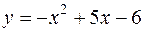 ;
; 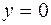 .
.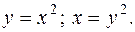
 .
.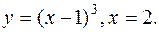
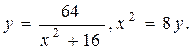
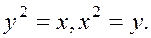

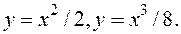

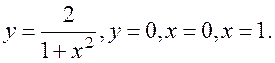
 .
.
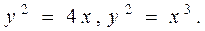
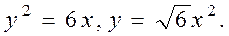


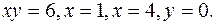

 ;
; 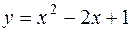 ;
; 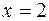 ,
, 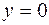 .
.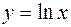 ;
; 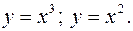

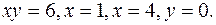

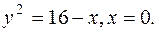
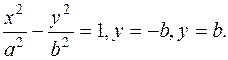
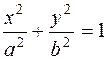 .
.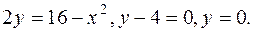
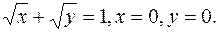
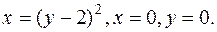

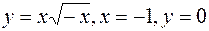 .
.