
|
|
Элементарная теория погрешностейПричины погрешностей. Для правильного понимания подходов и критериев, используемых при решении прикладных задач с применением ЭВМ, важно с самого начала признать, что получить точное решение задачи невозможно и не в этом цель вычислений. Получаемое решение y* почти всегда (за исключением некоторых весьма специальных случаев) содержит погрешность, т.е. является приближенным. Наличие погрешности решения обусловлено рядом весьма глубоких причин. Перечислим их. 10. Математическая модель является лишь приближенным описанием реального процесса. Погрешность, возникновение которой обусловлено данной причиной назовем погрешностью модели. 20. Исходные данные, как правило, содержат погрешности, поскольку они получаются в результате эксперимента (измерений), либо являются результатом решения некоторой вспомогательной задачи. Соответствующую погрешность назовем погрешностью исходных данных. Две перечисленные погрешности называют неустранимыми, т.к. они не могут быть устранены в дальнейших вычислениях. 30. Применяемые численные методы в большинстве случаев являются приближенными. Этот факт порождает погрешность метода. 40. При вводе исходных данных в ЭВМ, выполнении арифметических операций и выводе результатов производится округление вследствие конечности разрядной сетки ячеек ЭВМ. Полученная таким образом погрешность называется погрешностью округления или вычислительной погрешностью. Выводы и рекомендации. Таким образом, полная погрешность результата решения задачи на ЭВМ складывается из неустранимой погрешности и погрешностей метода и округления. Хотя, как было сказано, повлиять на неустранимую погрешность в процессе вычислений невозможно, это отнюдь не означает, что оценка ее величины не нужна. Достоверная информация, по крайней мере, о порядке величины неустранимой погрешности позволит осознанно выбрать метод решения задачи и разумно задать его точность. Желательно, чтобы величина погрешности метода dМ была в 2 – 10 раз меньше неустранимой погрешности. Большее значение dМ ощутимо снижает точность результата, меньшее – обычно требует увеличения затрат вычислительных ресурсов, практически уже не влияя на значение полной погрешности. Величина вычислительной погрешности dВ в основном определяется характеристиками используемой ЭВМ. Желательно, чтобы dВ была хотя бы на порядок меньше, чем dМ и крайне не желательно, чтобы dВ > dМ. Количественная оценка погрешности. Значащие и верные цифры. Пусть а – точное (вообще говоря, неизвестное) значение некоторой величины, а* – известное приближенное значение той же величины. Ошибкой или погрешностью приближенного числа а* называется разность а – а*. Количественными мерами ошибки являются абсолютная D = |а – а*| и относительная d = D / | a | погрешности. Так как значение а неизвестно, то непосредственное вычисление D и d по приведенным формулам невозможно. Более реальная задача состоит в получении некоторых верхних оценок В литературе по методам вычислений широко используется термин “точность”. Так, принято говорить о точности входных данных и решения, о повышении и снижении точности вычислений и т.д. Точность в качественных рассуждениях обычно выступает как противоположность погрешности, хотя для их количественного измерения выступают одни и те же характеристики. Точное значение величины – это значение, не содержащее погрешности. Повышение точности воспринимается как уменьшение погрешности, а снижение точности – как увеличение погрешности. Часто используемая фраза “найти решение с заданной точностью e” означает, что ставится задача о нахождении приближенного решения, принятая мера погрешности которого не превышает заданной величины e. Пусть приближенное число а* записано в виде десятичной дроби: а* = anan–1 …a0 . b1 b2 … bm. Значащими цифрами числа а* называются все цифры в его записи, начиная с первой ненулевой слева. Пример 1.1. У чисел а* = 0.0103 и а* = 0.0103000 значащие цифры подчеркнуты. Первое число имеет 3, а второе – 6 значащих цифр. Значащую цифру называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре. Замечание. Верная цифра приближенного числа, вообще говоря, не обязана совпадать с соответствующей цифрой в записи точного числа, так что термин “верная цифра” не следует понимать буквально. Пример 1.2. Пусть а = 1.0000; а* = 0.9999. Тогда D = 0.0001, т.е., согласно определению, у числа а* все значащие цифры – верные, хотя они не совпадают с соответствующими цифрами в записи точного числа. Количество верных цифр результата расчетов диктует правило, определяющее формат выводимых данных. Очевидно, что число значащих цифр, задаваемых в программе в процедурах вывода должно по возможности совпадать с числом верных цифр ответа. Подобное правило позволит правильно оценить качество результата и степень доверия к нему. Фраза “по возможности” употребляется в данном случае в связи со сложностью определения точного числа значащих цифр, как, впрочем, и многих других характеристик найденного решения. Одна из целей изучения вычислительных методов и состоит в достижении понимания того, что можно, а чего нельзя ожидать от результатов, полученных на ЭВМ. Погрешность арифметических операций. Исследуем влияние погрешностей исходных данных на погрешность результатов арифметических операций. Пусть а* и b* – приближенные значения чисел а и b. Утверждение 1.1. Абсолютная погрешность алгебраической суммы не превосходит суммы абсолютных погрешностей слагаемых, т.е. D(a* ± b*) £ D(a*) + D(b*). Данное соотношение легко выводится из свойства модуля суммы и разности. Несколько сложнее обстоит дело с величиной относительной погрешности. Утверждение 1.2. Пусть а и b – ненулевые числа одного знака. Тогда справедливы неравенства d(a* + b*) £ dmax; d(a* – b*) £ m×dmax, где dmax = max { d(a*), d(b*) }; m = |a + b| / |a – b|. Первое неравенство означает, что при суммировании чисел одного знака потери точности не происходит. При вычитании же чисел одного знака относительная ошибка возрастает в m > 1 раз и возможна существенная потеря точности. Так, если числа а и b близки настолько, что |a + b| >> |a – b|, то m >> 1 и не исключена полная потеря точности. Пример 1.3. Пусть при х = 1/1490 на 7-разрядной вычислительной машине (обычная точность ЭВМ 3-го поколения при использовании языка Фортран) вычисляется значение выражения y = a – b = cos x – cos 2x. Имеем a* = 0.9999998, b* = 0.9999991. Следовательно, y* = 7 ´ 10 – 7 = 0.0000007. То есть при 7 верных значащих цифрах исходных данных, когда d(a*) » d(b*) » 0.00001%, в результате имеем 1 верную значащую цифру, т.е. d(у*) »14.8%. Виновником катастрофической потери точности является предложенный метод решения задачи, в котором результат получается с помощью вычитания двух близких чисел. Вычисление по эквивалентной формуле Если для решения предлагаемой задачи нет подходящего метода, позволяющего исключить подобное вычитание, то для получения приемлемого результата следовало бы вычислить а и b с существенно большим числом верных цифр. Общий вывод. Выполнение арифметических операций над приближенными числами, как правило, сопровождается потерей точности. Единственная операция, при которой потери не происходит – сложение чисел одного знака. Наибольшая потеря точности может произойти при вычитании близких чисел одного знака. Особенности машинной арифметики. До сих пор речь шла об общих свойствах погрешностей вычислений, не зависящих от их аппаратной реализации. Однако применение ЦЭВМ имеет свои особенности, знание которых необходимо для его грамотного использования при решении научно-технических задач. В ЭВМ представимы не все числа, а лишь конечный набор рациональных чисел специального вида. Эти числа образуют представимое множество чисел вычислительной машины. Для всех остальных чисел возможно лишь их приближенное представление с ошибкой, которую называют ошибкой представления (или ошибкой округления). Обычно приближенное представление числа х в ЭВМ обозначают х* = fl(x). Обычно округление происходит по дополнению: если отбрасываемая цифра меньше 5, то сохраняемые цифры не меняются, если больше, то в младший сохраняемый разряд добавляется единица. В этом случае оценка относительной погрешности равна единице первого отброшенного разряда: d(х*) = eМ = 2–t , где t – число разрядов мантиссы в представлении числа с плавающей точкой. Величина eМ играет в вычислениях на ЭВМ фундаментальную роль; ее называют относительной точностью ЭВМ, а также машинным ипсилон. Его величину можно оценить непосредственно в ходе вычислительного процесса. Для этого достаточно включить в программу следующий фрагмент: e1 := 1.0; repeat e1 := e1 / 2.0; until р + e1 = р; epsilon := 2*e1;
Здесь р – вычисляемая величина, относительно которой и определяется машинное ипсилон. Отметим, что среди представимых на ЭВМ чисел нет не только ни одного иррационального, но и даже таких широко используемых в вычислениях чисел, как 0.1 и 0.01, поскольку их точные двоичные представления бесконечны, и они всегда записываются в памяти ЭВМ приближенно, с погрешностью, вызванной необходимостью округления. Эту особенность надо всегда учитывать. Для иллюстрации рассмотрим следующий пример программы. Пример 1.4. var x, b, s, h, s1, y : real; i, n : integer; begin {1-й блок} x := 0; s := 0; b := 10.7; h := 0.01; repeat s := s + 1/(x – b); x := x + h; until x >= b; writeln('x = ',x,' s= ',s:10); {2-й блок} n := round(b/h); s1 := 0; for i := 0 to n do begin х := i*h; s1 := s1 + 1/(х – b); end; writeln; writeln('n= ',n,' х = ',х,' s1= ',s1:10); readln; End. В обоих блоках вычисляются значения функции Из особенности машинного представления вещественных чисел (типа Real), в частности из необходимости их округления, следует, что операция сравнения двух вещественных чисел по совпадению некорректна. Иными словами, применение оператора вида “if x = b then…” скорее всего, приведет к тому, что используемое в нем логическое выражение будет почти всегда ложно. По той же причине в обоих блоках примера 1.4. не происходит переполнения, поскольку ни одно из значений х* и у* не совпадает с b, хотя их точные значения х и у в конце цикла равны b. В тех же случаях, когда логика алгоритма требует проверки совпадения, рекомендуется использовать следующий оператор “if abs(x – b) <= eps then…”, где значение eps достаточно мало, но существенно больше машинного ипсилон. Например, можно положить eps := 1.0e–6. Отметим, что сравнение по совпадению целых чисел (типа Integer) происходит корректно. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ 1. Вычислите значение машинного ипсилон в языке PASCAL при р = 1. Объясните, почему в алгоритме используется деление именно на 2, а не на другое число. 2^. Длина стороны квадрата a = 1, её приближенное значение a* задано с погрешностью D = ±0.1. Какова абсолютная погрешность площади квадрата? 3^. Приведите пример операции сложения, в котором из-за погрешности округления нарушается свойство коммутативности сложения. 4. Проведите расчеты по программе примера 1.4 и объясните столь большую разницу в ответах, полученных в 1 и 2 блоках. 5. Пусть необходимо вычислить значения некоторой функции f(x) на интервале [а, b] c шагом h. Выведете формулу для изменения аргумента х, представляющую собой обобщение аналогичной формулы х := i*h из второго блока примера 1.4. То же задание, когда задан не шаг h, а число n равноотстоящих точек на отрезке [а, b], х1 = а, xn = b.
Примеры решения заданий 2. Площадь квадрата S = a2. Отсюда S* = (a ± D)2 = (1 ± 0.1)2. Поскольку знак погрешности неизвестен, то надо найти оба значения S*: S*1 = 1.21; S*2= 0.81. Соответствующие погрешности площади равны: DS*1 = 0.21; DS*2 = 0.19. Т.к. вычисляется верхняя оценка погрешности, то берём максимум из двух чисел. Ответ: DS* = 0.21. 3. Нарушение коммутативности сложения: x = 349.7, y = 360.7, z =193.3. Округляем до целых после каждого действия: 349.7 + 360.7 = 710.4 » 710; 710 + 193.3 = 903.3 » 903. 193.3 + 360.7 = 554; 554 + 349.7 = 903.7 » 904.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
и 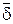 для соответствующих погрешностей.
для соответствующих погрешностей.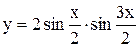 позволяет избежать такого вычитания и дает результат с 7 верными значащими цифрами у* = 6.756451 ´ 10 – 7.
позволяет избежать такого вычитания и дает результат с 7 верными значащими цифрами у* = 6.756451 ´ 10 – 7. на интервале [0, b] c шагом h = 0.01 при b = 10.7, и результаты суммируются. В первом случае изменение значения х происходит посредством его наращивания, т.е. с помощью оператора x := x + h. При этом, вследствие накопления ошибок округления, последнее значение х* превосходит 10.7 и составляет х* » 10.71. Во втором блоке используется более точная формула y := i*h, при этом последнее значение у* » 10.7, т.е. “заступа” не происходит. За счет такого различия в методе изменения аргумента значения s и s1 отличаются даже знаком. В дальнейшем рекомендуем применять для изменения аргумента в цикле формулу второго типа (см. задание 6).
на интервале [0, b] c шагом h = 0.01 при b = 10.7, и результаты суммируются. В первом случае изменение значения х происходит посредством его наращивания, т.е. с помощью оператора x := x + h. При этом, вследствие накопления ошибок округления, последнее значение х* превосходит 10.7 и составляет х* » 10.71. Во втором блоке используется более точная формула y := i*h, при этом последнее значение у* » 10.7, т.е. “заступа” не происходит. За счет такого различия в методе изменения аргумента значения s и s1 отличаются даже знаком. В дальнейшем рекомендуем применять для изменения аргумента в цикле формулу второго типа (см. задание 6).