
|
|
Этапы решения инженерной задачи с использованием ЭВМРешение серьезной инженерной задачи с использованием ЭВМ – достаточно длительный и сложный процесс. С определенной степенью условности его можно разбить на ряд последовательных этапов. 1. Постановка проблемы. Первоначально прикладная задача бывает сформулирована в слишком общем или расплывчатом виде: исследовать данное явление, спроектировать устройство, обладающее заданными свойствами, спрогнозировать поведение данного объекта и т.п. На первом этапе происходит конкретизация постановки задачи, формулируется цель исследования, так, чтобы найденное решение было полезным и в то же время могло быть получено с помощью существующих методов и в реальные сроки. 2. Выбор известной или построение новой математической модели, описывающей исследуемый объект или явление. Цель исследования ставит задачу словесно, или неформально. Для решения же задачи с помощью ЭВМ необходимо дать ее формализованное описание на языке математики, с помощью формул, графиков или иных математических объектов, которые связывают между собой исходные данные и результаты счета. Такое формализованное описание называют математической моделью объекта. В качестве примера можно привести любую школьную задачу по математике. Обычно такие задачи имеют два вида: прикладные задачи, формулируемые словесно (бригада рабочих копает яму, один рабочий может вырыть яму за 15 дней и т.д.) и числовые примеры (решить уже составленное уравнение, преобразовать выражение и т.п.). Задачи второго вида сформулированы математически, т.е. для них уже имеется модель (которая, возможно, что-то описывает) и надо выполнить определенные действия с этой моделью. В задачах же первого вида модель еще предстоит построить, т.е. что-то надо обозначить за х или у, составить одно или несколько уравнений, которые затем требуется решить. Процесс составления подобных соотношений, т.е. модели, и составляет содержание данного этапа. Часто имеется возможность выбора подходящей модели среди известных и принятых для описания соответствующих процессов, но нередко требуется и существенная модификация известной модели, а иногда необходимо создание принципиально новой модели. 3. Постановка вычислительной задачи. Чтобы уяснить понятие вычислительной задачи, рассмотрим пример. Необходимо найти значения двух интегралов:
Интегрирование по частям приводит нас к системе разностных уравнений I(n) = (n / 2) [ I(n – 1) + K(n – 1)], K(n) = (n / 2) [– I(n – 1) + K(n – 1)]. Для поиска начальных условий воспользуемся известными формулами:
Таким образом, в результате преобразований проблема свелась к решению достаточно стандартной задачи – системы разностных уравнений с известными начальными условиями. Подобные типовые задачи, которые уже не требуют каких-то аналитических выкладок, а сводятся лишь к более или менее простым вычислениям, называются вычислительными задачами. Таковыми можно считать расчет по набору явных формул, решение одного или системы алгебраических или дифференциальных уравнений, операции с матрицами, минимизация функции одной или нескольких переменных и др. 4. Выбор известного или построение нового численного метода. Поставленная вычислительная задача, несмотря на свою “типичность”, может быть очень сложной и поэтому нужны специальные численные методы ее решения. Перечислим две особенности численных методов, отличающих их от аналитических методов, используемых Вами, например, в курсе высшей математики. 1. Обычно численные методы сводятся к замене (как правило – приближенной) исходной сложной задачи одной или несколькими более простыми, для которых известны методы решения. 2. Ответ получается либо в результате выполнения набора конечных операций, либо как предел некоторой бесконечной числовой последовательности (подробнее о классах численных методов будет изложено в п. 4). Для решения одной и той же вычислительной задачи обычно может быть использовано несколько методов. Необходимо знать особенности этих методов, критерии, по которым оценивается их качество, чтобы выбрать наиболее эффективный способ решения проблемы. Кроме того, необходима определенная эрудиция в области существующих численных методов, чтобы иметь возможность в них ориентироваться. Данные обстоятельства свидетельствуют в пользу необходимости изучения специалистами в области технических дисциплин основ вычислительной математики. 5. Алгоритмизация и программирование. Как правило, выбранный на предыдущем этапе численный метод, содержит только принципиальную схему решений задачи, не включающую многие детали, без которых невозможна реализация метода на ЭВМ. Детальная проработка всех этапов численной схемы позволяет разработать алгоритм решения вычислительной задачи. Составление программы сводится к переводу этого алгоритма на выбранный язык программирования. 6. Отладка программы. Основу этого этапа составляет тестирование программы – проверка ее правильности на специально подготовленных тестовых задачах, имеющих известные решения. Подчеркнем важность тщательной подготовки тестовых задач. Как пишет в своей классической книге “Надежность программного обеспечения” Г. Майерс, ни в коем случае не следует использовать в качестве тестов “случайные наборы данных, которые можно тут же после использования выбросить, если, конечно, вы не хотите следом за ними выбросить и саму программу”. 7. Счет по программе. Обработка и интерпретация результатов. Полученные в результате расчетов необработанные выходные данные, как правило, представляют собой большие массивы чисел, содержательная интерпретация которых практически непосильна для человека. Поэтому обработку полученных результатов также рекомендуется возложить на ЭВМ. Зачастую первоочередной интерес представляет лишь небольшая часть полученной информации (например, значение одной из функций в выделенных точках) или некоторая, пусть даже грубая, интегральная характеристика объекта. Для того чтобы исследователь мог воспользоваться результатами расчетов, их необходимо представить в виде компактных таблиц, графиков или в иной удобной для восприятия форме. При этом надо максимально использовать возможности ЭВМ для подготовки такой информации. В заключение процитируем два основных тезиса, выдвинутых Р. В. Хеммингом еще в 60-х годах 20 столетия, и которыми, по нашему глубокому убеждению, следует постоянно руководствоваться при решении прикладных задач: - прежде, чем считать – подумай, что будешь делать с ответом; - цель расчетов – не числа, а понимание.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ 1. Для следующих прикладных задач постройте математическую модель проблемы, сформулируйте вычислительную задачу, найдите решение. 1.1.^ Имеется фанерный круг заданного диаметра D (рис.1.1). Выпилить из него прямоугольник максимальной площади.
1.2.^ Футболист, стоя на песчаном пляже, держит в руках мяч на высоте h0 = 1 м над землей. Затем он ударом ноги посылает мяч вертикально вверх с начальной скоростью v0 = 20 м/сек. На какой высоте над землей будет находиться мяч через 1, 2, 5 сек?
Примеры решения заданий
1.1. 1. Обозначим X и Y – ширину и высоту прямоугольника. Тогда его площадь равна S = X×Y. Однако размеры прямоугольника не могут быть произвольными, – он должен быть вписан в круг данного диаметра. Поэтому, если, например, Х известно, то Y по теореме Пифагора должно удовлетворять условию: X2 + Y2 = D2. Приведённые соотношения представляет собой формализованную запись условий задачи, т.е. её математическую модель.
2. Составим вычислительную задачу. Выразим Y из уравнения (2) и подставим полученное выражение в (1). Получим функцию одной переменной Х:
Для поиска экстремума функции одной переменной возьмём её производную и приравняем к 0:
Приведём к общему знаменателю, получим уравнение D2 – 2 X2 = 0, решение которого является требуемой вычислительной задачей. 3. Ответ:
1.2. 1. Очевидно, в математическую модель проблемы будет входить уравнение свободного падения, согласно которому высота над землёй брошенного тела через t сек равна H(t) = h0 + v0 t – Однако, уравнение (3) не учитывает, что если t достаточно велико, то при отсутствии отскока (футболист стоит на песчаном пляже), высота буде равна 0, т.к. мяч будет лежать на земле. Проще всего это условие можно учесть из уравнения (3). Если из него получим, что H(t) £ 0, то это будет означать, что мяч лежит на земле и ответом задачи будет 0. Окончательно получаем следующую модель:
где H(t) вычисляется по формуле (3). Расчёт по формулам (3), (4) представляет собой искомую вычислительную задачу. Ответ: через 1 сек h = 16.096 м, через 2 сек h = 21.386 м, через 5 сек h = 0 м.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ;
;  , n ³ 0, n – целое.
, n ³ 0, n – целое. ;
; .
.
 – математическая модель проблемы.
– математическая модель проблемы. .
.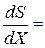
 = 0.
= 0.
 . (3)
. (3) , (4)
, (4)