
|
|
Теорема сложения вероятностейСуммой событий Аналогично определяется сумма нескольких событий. Теорема. Если
Следствие. Если
Пример 1. Среди лотерейных билетов 10 билетов с выигрышем по 100 рублей и 5 билетов с выигрышем по 500 рублей. Какова вероятность выигрыша при покупке одного билета? Решение.Обозначим события
События
Теорема. Сумма вероятностей попарно несовместных событий
Определение. Противоположными называют два единственно возможных события, образующих полную группу. Обозначение:
Пример 2. В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди двух наудачу извлеченных деталей есть хотя бы одна стандартная. Решение.Событие
Теорема умножения вероятностей Произведением двух событий Аналогично определяется произведение нескольких событий. Определение. Вероятность события Обозначение: Пример 3. Студент знает 25 вопросов из 30. Какова вероятность того, что он знает второй вопрос в билете, если а) он знает ответ на первый вопрос, б) он не знает ответа на первый вопрос? Решение. а) Событие
б) Событие
Теорема. Вероятность совместного появления событий
Пример 3*.В условиях предыдущей задачи найти вероятность того, что студент знает оба вопроса в билете. Решение. . Определение. Событие
Если
Пример 3. Студент выучил 20 билетов из 25 по математике и 17 из 20 по физике. Какова вероятность того, что он сдаст оба экзамена? Решение. Следствия из теорем сложения и умножения Теорема сложения вероятностей совместных событий Два события называются совместными, если появление одного из них не исключает появление других в одном и том же испытании. Теорема. Вероятность появления хотя бы одного из совместных событий равна
Пример 2*. (Условие см. выше) Решение.События:
Формула полной вероятности Теорема. Вероятностьсобытия
Пример 4. В группе спортсменов 20 лыжников, 6 велосипедистов, 4 бегуна. Вероятность выполнить классификационную норму такова: для лыжника – 0,9, для велосипедиста – 0,8, для бегуна – 0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму. Решение.
Вероятность гипотез. Формула Байеса Пусть событие
Пусть событие
Таким образом, получаем формулы Байеса, или формулы вероятностей гипотез, (1764 г.):
или
Пример 4*. (Условие см. выше). Найти вероятность того, что спортсмен, выполнивший норму, является бегуном. Решение.
Формулы Байеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие Схема Бернулли Пусть производится Найдем вероятность того, что при Вероятность одного события:
Число таких событий равно
Полученная формула носит название формулы Бернулли. Пример 5. В цехе 6 моторов. Для каждого мотора вероятность того, что он включен, равна 0,8. Найти вероятность того, что в данный момент: а) включено 4 мотора, б) включены все моторы, в) выключены все моторы Решение. Имеем а) по формуле Бернулли при
б) по формуле Бернулли при
в) по формуле Бернулли при
Если число испытаний Если вероятность появления события
Функция Таким образом, получаем
Пример 5. Найти приближенно вероятность того, что при 400 испытаниях событие наступит ровно 104 раза, если вероятность его появления в каждом испытании равна 0,2. Решение. По условию, Воспользуемся формулой Лапласа
По таблице находим
Интегральная теорема Лапласа: Если вероятность наступления события
где Функция Лапласа Свойства функции Лапласа. 1о. 2о. При Таким образом, получаем
где Пример 6. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена а) не менее 70 и не более 80 раз; б) не более 70 раз. Решение. а) По условию, Воспользуемся интегральной теоремой Лапласа:
Таким образом, имеем
б) По условию, Воспользуемся интегральной теоремой Лапласа:
Таким образом, имеем
С помощью функции Лапласа можно вычислить вероятность отклонения относительной частоты от постоянной вероятности:
Пример 7. Вероятность появления события в каждом из 10 000 независимых испытаний равна 0,75. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,001. Решение.По условию, Требуется найти вероятность
Получим Пример 8. Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти, какое отклонение относительной частоты появления события от его вероятности можно ожидать с вероятностью 0,9128 при 5000 испытаниях. Решение.По условию, Так как
По таблице находим, что 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
и  называют событие
называют событие  , состоящее в появлении хотя бы одного из событий.
, состоящее в появлении хотя бы одного из событий. .
. – попарно несовместные события, то
– попарно несовместные события, то .
. ,
,  .
. .●
.● .
. – событие, противоположное событию
– событие, противоположное событию 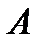 .
. .
. – общее число исходов,
– общее число исходов, – число исходов благоприятствующих событию
– число исходов благоприятствующих событию  ,
, . ●
. ● , состоящее в совместном появлении этих событий.
, состоящее в совместном появлении этих событий.
 .
. .●
.● .
. .●
.● .
. .
. .●
.● .
. .
. .●
.●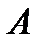 , которое может наступить лишь при условии появления одного из несовместных событий
, которое может наступить лишь при условии появления одного из несовместных событий 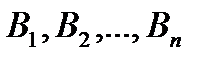 , образующих полную группу, равна
, образующих полную группу, равна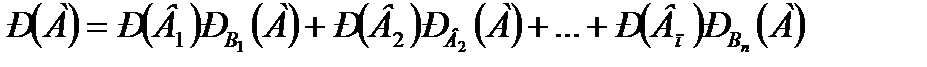 .
. ,
, .●
.●



 .
.






 .●
.● независимых испытаний, в каждом из которых вероятность появления события
независимых испытаний, в каждом из которых вероятность появления события 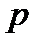 – испытания в схеме Бернулли. Обозначим вероятность ненаступления события
– испытания в схеме Бернулли. Обозначим вероятность ненаступления события  .Очевидно, что
.Очевидно, что  .
. раз. Обозначим эту вероятность
раз. Обозначим эту вероятность  .
. раз равна
раз равна .
. . Так как эти события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме всех возможных сложных событий. Поскольку вероятности этих событий равны между собой, то их сумма равна вероятности одного события, умноженной на их число.
. Так как эти события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме всех возможных сложных событий. Поскольку вероятности этих событий равны между собой, то их сумма равна вероятности одного события, умноженной на их число.
 ,
,  ,
,  .
.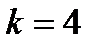 получим
получим
 .
. получим
получим .
. получим
получим .●
.● , где
, где  .
. задается таблицами для
задается таблицами для  ,
,  – четная функция, т.е.
– четная функция, т.е. 
 .
.
 при
при  ,
,  ,
,  ,
,  .
.

 .
. .
. .
.
 .●
.● до
до  раз приближенно равна
раз приближенно равна
 ,
, ,
, 


 .
.
 0,5.
0,5.
 ,
, ,
,  ,
, 
 ,
,  .
.

 ;
;
 .
.



 .
. ,
, 

 ;
; .
.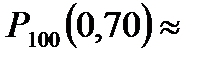




 .●
.● .
. ,
,  .
. .
. .
. .●
.● ,
,  ,
,  .
. или
или ,
,  .
. при
при  . Значит,
. Значит,  и
и  .●
.●