
|
|
Канонические уравнения метода силВ заданной системе по направлениям имеющихся жестких связей, в том числе и тех связей, которые отброшены при переходе к основной системе, перемещений быть не может, поэтому и в основной системе перемещения по направлениям отброшенных связей должны равняться нулю. А для этого реакции отброшенных связей должны иметь строго определенные значения. Условие равенства нулю перемещения по направлению любой i-ой связи из n отброшенных на основании принципа независимости действия сил имеет вид:
где первый индекс означает направление перемещения и номер отброшенной связи, а второй указывает на причину, вызвавшую перемещение, т.е. В методе сил реакцию k-ой связи принято обозначать через
где одинаковые индексы ( Вид уравнения (14.5), т.е. количество слагаемых в каждом из них и их общее число, определяется только степенью статической неопределимости системы и не зависит от ее конкретных особенностей.
28. Алгоритм расчета методом сил Независимо от особенностей рассматриваемой конструкции, можно выделить следующую последовательность расчета статически неопределимых систем методом сил: 1. Определить степень статической неопределимости. 2. Выбрать основную систему. 3. Сформировать эквивалентную систему. 4. Записать систему канонических уравнений. 5. Построить единичные и грузовые эпюры внутренних силовых факторов, возникающих в элементах рассматриваемой конструкции. 6. Вычислить коэффициенты при неизвестных и свободные члены системы канонических уравнений. 7. Построить суммарную единичную эпюру. 8. Выполнить универсальную проверку коэффициентов при неизвестных и свободных членов. 9. Решить систему канонических уравнений, т.е. определить реакции лишних связей. 10. Построить эпюры возникающих внутренних силовых факторов для заданной системы (иначе говоря, окончательные эпюры). 11. Выполнить статическую и кинематическую проверки.
29. Статическая проверка правильности эпюр М, Q и N заключается в составлении условий статического равновесия всей рамы в целом, ее узлов и отдельных произвольно выделенных частей рамы. Например, должны равняться нулю сумма проекций на вертикаль всех опорных реакций рамы и внешней нагрузки, сумма моментов всех реакций и внешней нагрузки относительно любой точки и т. д.
Рис. 15.12 Проверим равновесие рамы, показанной на рис. 14.12, а. Эпюры М, Q и N для этой рамы изображены на рис. 14.12, в, г, д. На рис. 15.12, а показаны все действующие на раму опорные реакции и заданная нагрузка. Составим уравнения равновесия:
Сумма моментов сил относительно опорного шарнира
Таким образом, условия равновесия рамы удовлетворяются. Проверка эпюры Q производится, кроме того, путем сопоставления ее с эпюрой М. Так, например, в сечении, гдекасательная к эпюре М параллельна оси элемента, поперечная сила Q должна равняться нулю; в тех сечениях прямого стержня, где касательная к эпюре М наклонена к оси в одну и ту же сторону, поперечная сила Q должна иметь одинаковые знаки; из двух сечений элементов в том, в котором касательная к эпюре М образует с осью элемента больший угол, имеется и большая поперечная сила и т. д. Этим требованиям удовлетворяют эпюры Q и Статическая проверка эпюр М, Q и Ошибки в найденных значениях неизвестных в большинстве случаев можно обнаружить с помощью так называемой деформационной проверки, сущность которой рассмотрим на примере рамы, изображенной на рис. 14.12, а. Отбросив из заданной рамы две связи, препятствующие перемещению ее нижнего конца, превратим раму в статически определимую систему (рис. 15.12,б). Приложим к этой системе реакции НА и RA отброшенных связей и заданную нагрузку (рис. 15.12, б); эпюра изгибающих моментов и перемещения в статически определимой системе от этих реакций и нагрузки будут в точности такие же, как и в заданной раме (рис. 14.12, я). Вычислим для проверки перемещение Аверт нижнего конца статически определимой рамы по вертикали; оно должно равняться нулю, так как в заданной раме этот конец опирается на шарнирно неподвижную опору. Для этого построим единичную эпюру изгибающих моментов М от единичной силы, действующей по направлению искомого перемещения (рис. 15.12, а). Перемножим эту эпюру с окончательной эпюрой М (см. рис. 14.12, в):
Проверим теперь, равно ли нулю горизонтальное перемещение
Таким образом, деформационная проверка производится в следующем порядке. 1. Заданная статически неопределимая система отбрасыванием лишних связей превращается в статически определимую. 2. По направлению каждой отброшенной связи прикладывается единичная сила (или момент — если рассматриваемая связь препятствует повороту поперечного сечения). 3. От каждой такой силы (или момента) строится единичная эпюра изгибающих моментов М. 4. Путем умножения эпюры М на суммарную (окончательную) эпюру изгибающих моментов (для заданной системы) определяется перемещение в полученной статически определимой системе (см. п. 1) по направлению каждой отброшенной связи. 5. Если подсчитанные таким образом перемещения по направлению каждой отброшенной связи равны нулю, то это свидетельствует о правильности окончательной эпюры изгибающих моментов.
Рис. 16.12 Статически определимая система, применяемая при проверке перемещений (см. п. 1), не обязательно должна совпадать с той основной системой, которая использована при расчете конструкции. Более того, проверяться могут перемещения в различных статически определимых системах. Так, например, для проверки правильности окончательной эпюры моментов (см. рис. 14.12, в) можно определить горизонтальное смещение крайнего правого сечения рамы, используя статически определимую систему, изображенную на рис. 16.12, а, и поворот этого же сечения, используя систему, показанную на рис. 16.12, б. Для деформационной проверки можно использовать единичные эпюры изгибающих моментов в основной системе, построенные при расчете рамы. Проверка в этом случае сводится к перемножению каждой такой единичной эпюры с окончательной эпюрой изгибающих моментов. Результат каждого перемножения должен равняться нулю. При деформационной проверке эпюр определяются перемещения в заданной системе, значения которых известны (равны нулю). Аналогичным способом можно найти любые перемещения в заданной статически неопределимой системе. Определение их производится в следующем порядке. 1. Путем отбрасывания лишних связей заданная статически неопределимая система превращается в статически определимую. 2. По направлению искомого перемещения к полученной статически определимой системе прикладывается соответствующая ему единичная сила (при линейном перемещении — сосредоточенная сила, а при угле поворота — сосредоточенный момент). 3. От единичной силы строится единичная эпюра изгибающих моментов М в статически определимой системе. 4. Путем умножения эпюры М на суммарную (окончательную) эпюру изгибающих моментов (для заданной системы) определяется искомое перемещение.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (14.2)
(14.2)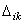 - это перемещение по направлению i-ой связи, вызванное реакцией k-ой связи;
- это перемещение по направлению i-ой связи, вызванное реакцией k-ой связи;  - перемещение по направлению i-ой связи, вызванное одновременным действием всей внешней нагрузки.
- перемещение по направлению i-ой связи, вызванное одновременным действием всей внешней нагрузки. . С учетом этого обозначения и в силу справедливости закона Гука перемещения
. С учетом этого обозначения и в силу справедливости закона Гука перемещения  (14.3)
(14.3) - единичное (или удельное) перемещение по направлению i-ой связи, вызванное реакцией
- единичное (или удельное) перемещение по направлению i-ой связи, вызванное реакцией  т.е. реакцией, совпадающей по направлению с Xk, но равной единице.
т.е. реакцией, совпадающей по направлению с Xk, но равной единице. ), и побочные (
), и побочные (  ). Главные перемещения всегда положительные, в отличие от побочных. Симметрично расположенные перемещения в соответствии с теоремой о взаимности перемещений равны друг другу, т.е.
). Главные перемещения всегда положительные, в отличие от побочных. Симметрично расположенные перемещения в соответствии с теоремой о взаимности перемещений равны друг другу, т.е.  , это свойство называется законом парности коэффициентов при неизвестных.
, это свойство называется законом парности коэффициентов при неизвестных.
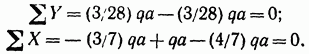

 построенные на рис. 14.12, в, г для статически неопределимой рамы.
построенные на рис. 14.12, в, г для статически неопределимой рамы. не может еще гарантировать правильности решения задачи, так как условия статики удовлетворяются и при неправильно найденных значениях неизвестных.
не может еще гарантировать правильности решения задачи, так как условия статики удовлетворяются и при неправильно найденных значениях неизвестных.
 нижнего конца рамы. Для этого перемножим эпюру М от единичной горизонтальной силы (рис. 15.12, г) с окончательной эпюрой М (см. рис. 14.12, в):
нижнего конца рамы. Для этого перемножим эпюру М от единичной горизонтальной силы (рис. 15.12, г) с окончательной эпюрой М (см. рис. 14.12, в):
