
|
|
Искусственное двойное лучепреломление12 Обычные прозрачные тела, не обладающие двойным лучепреломлением, тем не менее при определенном воздействии на них становятся двупреломляющими.
где σ – напряжение, k – коэффициент, зависящий от свойств вещества. Для наблюдения двойного лучепреломления исследуемое тело помещают между скрещенными поляризаторами, плоскости пропускания которых составляют угол 45° с направлением деформации (см. рис.). Если тело имеет вил пластинки или кубика, то при увеличении напряжения наблюдают усиление и ослабление прошедшего света.
Схема установки для наблюдения этого эффекта показана на рисунке. Между двумя скрещенными поляризаторами Р и Р' помещают ячейку Керра – исследуемую жидкость между обкладками конденсатора в кювете. При создании электрического поля, напряженность Е которого составляет угол 45° с плоскостями пропускания поляризаторов, среда становится оптически анизотропной, оптическая ось которой совпадает с направлением вектора
Эффект Керра объясняется тем, что при включении электрического поля происходит поляризация молекул вещества и их выстраивание по полю. Это и создает анизотропию вещества с преимущественным направлением – оптической осью – вдоль электрического поля. Наиболее важной особенностью эффекта Керра, обусловливающей его широкое применение, является весьма малая инерционность (до 10-12 с!). Это, в частности, позволяет осуществить практически безинерционный оптический затвор, с помощью которого изучают весьма быстро протекающие процессы. Кроме того, данный эффект используют для создания сверхкоротких световых импульсов. Этот эффект используют для управления режимом работы лазеров с целью получения сверхкоротких импульсов огромной мощности и во многих других весьма тонких физических экспериментах. Формула Рэлея-Джинса Рэлей и Джинс в 1900–1905 г. сделали попытку определить функцию спектрального распределения энергетической светимости, исходя из теоремы о равномерном распределении энергии по степеням свободы. Представим себе вакуумированую полость, стенки которой поддерживаются при постоянной температуре Т. В равновесном состоянии энергия излучения будет распределена в объеме полости с определенной плотностью, которая зависит только от температуры и не зависит от свойств стенок полости. Ученые исходили из того, что равновесное излучение в полости представляет собой систему стоячих волн. На каждое электромагнитное колебание приходится в среднем энергия, равная двум половинкам kT: ½kT – на электрическую, ½kT – на магнитную энергию волны (по классическим представлениям на каждую колебательную степень свободы приходится в среднем энергия, равная kT). Для функции спектрального распределения энергии равновесного излучения в полости, приходящуюся на диапазон длин волн dλ, Рэлей и Джинс получили формулу:
Или в зависимости от частоты света:
Формула Планка Формула Планка.Правильная формула для спектральной плотности энергетической светимости равновесного излучения, подтвержденная всеми экспериментальными исследованиями, была найдена Планком сначала полуэмпирическим путем. Спустя короткое время, Планк нашел теоретический вывод этой формулы, изложенный им 14 декабря 1900 г. на заседании Немецкого физического Общества. Этот день считается днем рождения квантовой физики. Гипотеза Планка состоит в том, что излучение и поглощение света веществом происходит не непрерывно, а дискретными порциями, называемыми квантами, величина которых пропорциональна частоте излучения. Энергия кванта: где Формула Планка может быть получена тем же методом, что и формула Рэлея-Джинса. Согласно Планку, энергия гармонического осциллятора может принимать не произвольные, а только избранные значения, образующие дискретный ряд:
Подставив выражение в формулу Рэлея-Джинса вместо kT, получим, что универсальная функция Кирхгофа принимает вид
И называется формула Планка.
В области больших длин волн

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Анизотропия при деформациях. При одностороннем сжатии или растяжении направление деформации становится выделенным и играет роль оптической оси. При одностороннем сжатии или растяжении направление деформации становится выделенным и играет роль оптической оси. Тело становится анизотропным и двупреломляющим, разность показателей преломления которого
Анизотропия при деформациях. При одностороннем сжатии или растяжении направление деформации становится выделенным и играет роль оптической оси. При одностороннем сжатии или растяжении направление деформации становится выделенным и играет роль оптической оси. Тело становится анизотропным и двупреломляющим, разность показателей преломления которого ,
, Анизотропия в электрическом поле. Возникновение двойного лучепреломления в жидкости и в аморфных телах под воздействием электрического поля – эффект Керра – нашел широкое применение как в науке, так и в технике эксперимента.
Анизотропия в электрическом поле. Возникновение двойного лучепреломления в жидкости и в аморфных телах под воздействием электрического поля – эффект Керра – нашел широкое применение как в науке, так и в технике эксперимента. . Возникающая разность показателей преломления обыкновенной и необыкновенной волн оказывается при этом равной
. Возникающая разность показателей преломления обыкновенной и необыкновенной волн оказывается при этом равной , где λ – длина волны света, В – постоянная Керра.
, где λ – длина волны света, В – постоянная Керра. .
.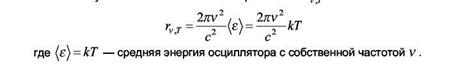
 Выражение получило название формулы Рэлея-Джинса. Эта формула удовлетворяет экспериментальным данным лишь при больших длинах волн (см. рис.). Интегрирование выражения по всем длинам волн в пределах от 0 до ∞ дает бесконечно большое значение. Отсюда следует, что по теории Рэлея-Джинса тепловое равновесие между излучением и веществом невозможно. Этот вывод, названный ультрафиолетовой катастрофой, противоречит опыту. Причина ультрафиолетовой катастрофы заключается в том, что в теории Рэлея-Джинса излучение в полости имеет бесконечное число степеней свободы, а вещество – конечное. Поэтому, если бы было справедливо равномерное распределение энергии по степеням свободы, то при тепловом равновесии вся энергия должна была бы сосредоточиться в излучении.
Выражение получило название формулы Рэлея-Джинса. Эта формула удовлетворяет экспериментальным данным лишь при больших длинах волн (см. рис.). Интегрирование выражения по всем длинам волн в пределах от 0 до ∞ дает бесконечно большое значение. Отсюда следует, что по теории Рэлея-Джинса тепловое равновесие между излучением и веществом невозможно. Этот вывод, названный ультрафиолетовой катастрофой, противоречит опыту. Причина ультрафиолетовой катастрофы заключается в том, что в теории Рэлея-Джинса излучение в полости имеет бесконечное число степеней свободы, а вещество – конечное. Поэтому, если бы было справедливо равномерное распределение энергии по степеням свободы, то при тепловом равновесии вся энергия должна была бы сосредоточиться в излучении.
 ,
, – постоянная Планка.
– постоянная Планка. Под осциллятором понимается не только частица, совершающая гармонические колебания, но, например, и стоячая волна определенной частоты в полости. Если осциллятор находится в полости, стенки которой поддерживаются при постоянной температуре, то наряду с излучением будут происходить и акты поглощения. Со временем установится вполне определенное состояние детального равновесия, в котором число актов излучения в среднем равно числу обратных актов поглощения. Планк доказал, что средняя энергия осциллятора может быть определена как
Под осциллятором понимается не только частица, совершающая гармонические колебания, но, например, и стоячая волна определенной частоты в полости. Если осциллятор находится в полости, стенки которой поддерживаются при постоянной температуре, то наряду с излучением будут происходить и акты поглощения. Со временем установится вполне определенное состояние детального равновесия, в котором число актов излучения в среднем равно числу обратных актов поглощения. Планк доказал, что средняя энергия осциллятора может быть определена как .
. .
.
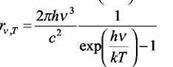
 , тогда
, тогда 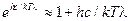 , и формула переходит в формулу Рэлея-Джинса.
, и формула переходит в формулу Рэлея-Джинса.