
|
|
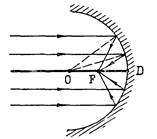
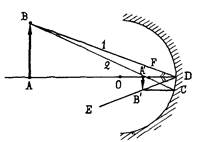
Понятие когерентности. Пространственная и временная когерентность волн.12 Преломление на сферических поверхностях.
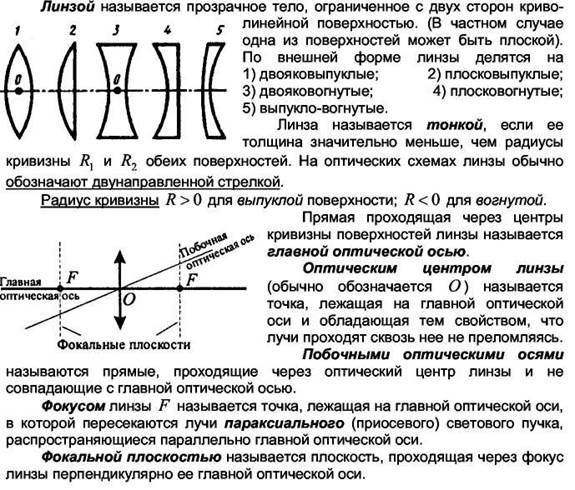
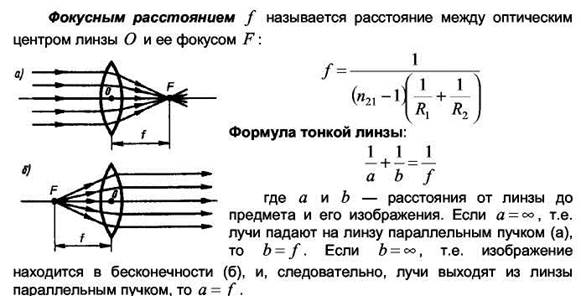
Линзы. Уравнение тонких линз
Понятие когерентности. Пространственная и временная когерентность волн. Когерентностью называют согласованное протекание волновых процессов. Степень согласованности называют степенью когерентности. Различают временную и пространственную когерентность. 1. Временная когерентность – обусловлена характером излучения естественных источников света. Когерентных источников в природе нет, их можно получить только делением одного источника на несколько. Излучение всегда связано с возбуждением атома в источнике. Если атом переходит из возбужденного состояния в невозбужденное, то происходит излучение фотона (квант света). В возбужденном состоянии атом находится ~10-8 c, затем излучается фотон, далее атом снова можно перевести в возбужденное состояние. Частота, амплитуда, направление и фаза колебаний каждого излучения атома могут быть различными. Поэтому даже излучение одного атома становится некогерентным по отношению к самому себе через время когерентности (ср. время жизни возбужденного атома). За это время атом излучает эл-маг. волну или цуг волн, длина которой называется длиной когерентности
На этом расстоянии волна когерентна по отношению к самой себе. Если для наблюдения интерференции источник делят на два световых пучка, то максимальная разность хода между ними примерно 3 м. Если больше, то они становятся некогерентными и интерференционной картины нет. Когерентность колебаний, которые совершаются в одной точке пространства, определяемая степенью монохроматичности, называется временной когерентностью. На качество интерференционной картины влияет степень немонохроматичности Если же источник состоит из совокупности различных атомов, то излучаемые длины волн будут лежать в широком диапазоне Как следует из формулы , ширина интерференционной полосы
Тогда максимальный порядок интерференции будет равен
В итоге длина когерентности будет определяться как
Для солнечного света lког~5λ, для лазеров lког составляет величину порядка сотен метров (иногда километров).
Два источника, размеры и взаимное расположение которых позволяют наблюдать интерференцию, называются пространственно-когерентными. При решении задач по интерференции рассматриваются точечные источники света. Однако реальные источники света имеют конечные размеры, что, несомненно, влияет на качество интерференционной картины. Увеличение размеров источника так же, как уменьшение степени монохроматичности, приводит к размытию интерференционных полос, и даже к их исчезновению. В большинстве опытов по интерференции в качестве источника света используется узкая щель (опыт Юнга, см. рис.). В этом случае интерференционную картину можно представить как наложение волн, идущих от отдельных бесконечно узких участков щели S. Таким образом, интервалы между соседними максимумами, от одного края щели будут заполняться максимумами от других частей щели. Если ширину щели сделать равной ширине интерференционной полосы
В нашем случае
где φ – угловая ширина щели относительно диафрагмы с вторичными источниками, λ – средняя длина волны. Если в качестве источника света использовать Солнце Таким образом, для наблюдения интерференции необходимо, чтобы выполнялись условия временной и пространственной когерентности. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|








 м – длина цуга электромагнитной волны, излучаемой источником из одного атома.
м – длина цуга электромагнитной волны, излучаемой источником из одного атома. световых волн, т.е. разброс длин волн. Идеальную монохроматическую волну получить практически невозможно, так как уровни энергии атома в возбужденном и невозбужденном состояниях представляют собой полосы определенной ширины. Поэтому частота излучения, а значит и длина волны, которые определяются разностью энергий этих уровней, меняются от одного акта излучения к другому.
световых волн, т.е. разброс длин волн. Идеальную монохроматическую волну получить практически невозможно, так как уровни энергии атома в возбужденном и невозбужденном состояниях представляют собой полосы определенной ширины. Поэтому частота излучения, а значит и длина волны, которые определяются разностью энергий этих уровней, меняются от одного акта излучения к другому.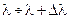 .
. . Таким образом, при образовании интерференционной картины интервал между соседними максимумами, соответствующими длине волны λ, будет заполняться промежуточными максимумами, соответствующими длинам волн из заданного диапазона. Следовательно, интерференционная картина будет размываться, и, в конце концов, может совсем исчезнуть. Это произойдет тогда, когда на месте максимума (m+1)-го порядка для длины волны λ окажется максимум m-го порядка для длины волны
. Таким образом, при образовании интерференционной картины интервал между соседними максимумами, соответствующими длине волны λ, будет заполняться промежуточными максимумами, соответствующими длинам волн из заданного диапазона. Следовательно, интерференционная картина будет размываться, и, в конце концов, может совсем исчезнуть. Это произойдет тогда, когда на месте максимума (m+1)-го порядка для длины волны λ окажется максимум m-го порядка для длины волны  , т.е.
, т.е. .
.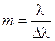 .
. .
. 2. Пространственная когерентность – вводится в связи с конечностью размеров реальных источников света.
2. Пространственная когерентность – вводится в связи с конечностью размеров реальных источников света. , то интерференционная картина полностью исчезнет.
, то интерференционная картина полностью исчезнет.  Это можно объяснить и тем, что вторичные источники S1 и S2 становятся некогерентными. В этом случае имеет смысл говорить о максимальном расстоянии dког между вторичными источниками, при котором они остаются когерентными – радиус когерентности. Из формулы получим
Это можно объяснить и тем, что вторичные источники S1 и S2 становятся некогерентными. В этом случае имеет смысл говорить о максимальном расстоянии dког между вторичными источниками, при котором они остаются когерентными – радиус когерентности. Из формулы получим .
. и
и  , тогда
, тогда ,
, , то
, то  . Обеспечить такое расстояние между двумя щелями практически невозможно.
. Обеспечить такое расстояние между двумя щелями практически невозможно.