|
|
Построение графиков функций в MatLab.Построение графика функции одной переменной. Построим график функции
Вывод графика функции состоит из следующих этапов: 1. Задание вектора значений аргумента x. Для того чтобы задать вектор, элементы которого, отличаются друг от друга на одинаковую величину (шаг), Используют двоеточие «:». Условно можно записать x = [начальное условие : шаг : конечное условие], если шаг равен 1, то его можно не указывать x = [начальное условие : конечное условие]. Для более точного построения графика функции следует задавать малый шаг при вводе вектора x. 2. Вычисление вектора y значений функции При этом операции в выражении для функции должны выполняться поэлементно. 3.Вызов команды plot(x, y) для построения графика. Создадим программу list_6
После выполнения команд на экране появляется окно Figure No. 1 с графиком функции в виде плавной кривой. Окно содержит меню, панель инструментов и область графика.
Оформление графиков.
Команда plot позволяет задать стиль, толщину и цвет линий, а также тип маркера. Приведем в таблице некоторые свойства линий:
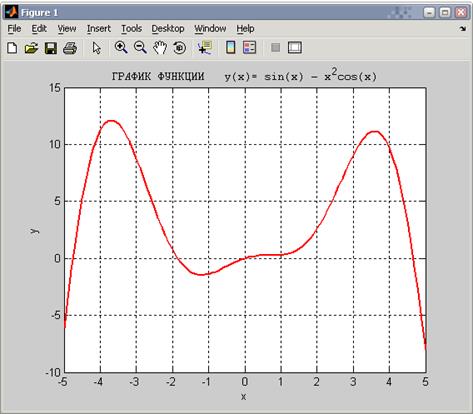
Построим график функции
Результатом выполнения программы будет график
Дополнительными элементами оформления графика являются: координатная сетка, подписи к осям, заголовок и легенда. Сетка наносится командой grid on. Подписи к осям размещаются при помощи команд xlabel, ylabel. Заголовок дается командой title. (Для использования русских букв в заголовке, в аргументе команды title следует изменить название шрифта на Courier.) Команда legend снабжает график информацией о линиях, размещенных на одних осях. Использование в аргументах команд некоторых математических обозначений в формате TeX позволяет добавлять формулы на график.
Внесем изменения в программу list_6:
В результате выполнения программы получим график
Сравнение нескольких функций можно производить, отобразив их графики на одних осях. Например, построим графики на отрезке
Текс программы list_7
В результате получим график
Примечание.Третий параметр в команде legend управляет размещением в графическом окне. (0 – система выбирает лучшее месть в поле графика; 1 – легенда размещается в правом верхнем углу, 2 – легенда размещается в левом верхнем углу; 3 – легенда размещается в правом нижнем углу, 4 – легенда размещается в левом нижнем углу).
Для расположения нескольких графиков на одних осях можно также использовать команду hold on. Команда plot(x, f, x, g) эквивалентна последовательности команд plot(x, f) hold on plot(x, g).
Внесем изменения в программу list_7
Результат работы программы:
Для размещения нескольких осей в одном графическом окне используется команда subplot, которая располагает графики в виде матрицы и используется с тремя параметрами: subplot(i, j, n), здесь iиj – число подграфиков по вертикали и горизонтали, а n – номер подграфика, который надо сделать текущим. Например, построим график табличной функции
и функции Программа list_8.
Результат работы программы:
Построение поверхностей в MATLAB. Пусть требуется построить график функции
на области определения Алгоритм построения включает этапы: 1. Разбиение области определения равномерной сеткой и создание матрицы с координатами узлов сетки. Сетка генерируется с помощью команды meshgrid: [X,Y] = meshgrid(-2:0.25:2,-2:0.25:2); 2. Вычисление значения функции Z = X.*exp(-X.^2 -Y.^2);
3. Использование одной из графических функций MATLAB – mesh или surf.
Для отображения каркасной поверхности используется функция mesh: mesh(X, Y, Z) Цвет линий поверхности соответствует значениям функции.
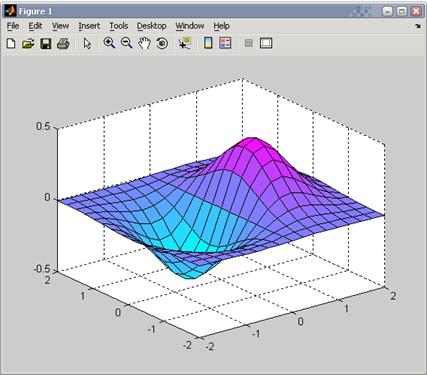
Функция surf строит каркасную поверхность и заливает каждую клетку определенным цветом, зависящим от значения функции в точках, соответствующим углам клетки: surf(X,Y,Z)
Команда colormap меняет палитру графического окна. Таблица палитры цветов.
Например, введем команду colormap('cool'). В результате получаем
Дополнительно, с помощью команды hidden off можно сделать каркасную поверхность видимой; shading flat можно убрать каркасные линии; shading interp можно изобразить поверхность, плавно залитую цветом; colorbar можно вывести рядом с графиком столбик, устанавливающий соответствие между цветом и значением функции.
Дополнительные элементы оформления графика являются такие как подписи к осям, заголовок и легенда выполняются так же как и при построении графиков функций одной переменной (см. Практика_MATLAB_3). Удаление координатной сетки выполняется командой grid off.
М-функции. Если в вычислениях часто используется некоторая функция Например, создадим функцию
Для этого открываем новый М-файл и набираем текст
Слово function в первой строке определяет, что данный файл содержит файл-функцию; myfun – имя функции; x – входной аргумент; f – выходной аргумент. Затем идет тело функции, которое состоит, в данном примере, из одной строки. Вообще, тело функции может состоять из нескольких строк, важно, чтобы окончательное значение функции записывалось в f. В конце ставиться «;» для подавления вывода лишней информации на экран. Сохраняем файл под именем функции myfun. Теперь созданную функцию можно использовать так же, как и встроенные функции sin, cos, и другие. Например, наберем в командной строке >> y = myfun(1.3) y = 0.51149 При создании функции использовались поэлементные операции, следовательно, её входным аргументом могут быть векторы, например, наберем в командной строке: >> x=[1.3 5.2] x = 1.3 5.2 >> y = myfun(x) y = 0.51149 -13.552 Построим график этой функции на отрезке Программа list_11
Результат работы программы – график функции
Интегрирование функций. Вычисление определенных интегралов В MatLab существует встроенная функция, реализующая алгоритм метода Симпсона с автоматическим выбором шага I = quad('имя функции', а, b) где имя функции – имя М-функции, задающей подынтегральное выражение; а, b – пределы интегрирования, I – значение интеграла. Для повышения точности вычислений следует задать дополнительный четвертый аргумент e – точность метода: I = quad('name', а, b, e). Например, требуется вычислить определенный интеграл
Сначала создадим файл-функцию, для вычисления подынтегрального выражения и сохраним её под именем fint
Затем в командном окне выполним команду I = quad('fint', -1, 1) В результате получим значение интеграла I = -0.66349
Вычисление интегралов от функций, заданных в виде таблицы. Пусть функция
Формула Симпсона для численного интегрирования имеет вид
Напишем М-функцию f_simps, реализующую алгоритм метода Симпсона в MatLab
Здесь: F – вектор значений табличной функции, M – четное число интервалов на которые разделён отрезок Например, для функции Выполняем в команды: M = 10; a = -1; b = 1; h = (b-a)/M; x = a:h:b; F = exp(-x).*sin(x); Int = f_simps(F, M, h)
Int = -0.6635 Вычисление двойных интегралов в MATLAB.
В MATLAB определена встроенная функция для приближенного вычисления двойных интегралов dblquad. Сначала следует написать файл-функцию для вычисления подынтегрального выражения а затем вызвать функцию в виде dblquad(’name’,a,b,c,d) где name – имя М-функции, задающей подынтегральное выражение; a,b, – верхний и нижний пределы интегрирования внутреннего интеграла по c,d – верхний и нижний пределы интегрирования внешнего интеграла по
Пример. Найдем значение двойного интеграла
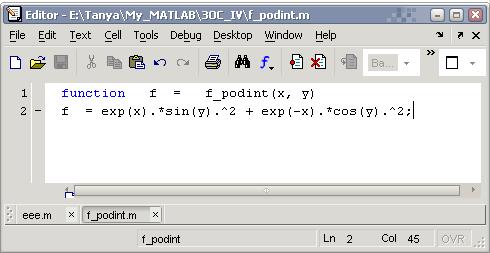
Создаем файл-функцию f_podint с двумя входными аргументами:
Теперь для вычисления интеграла вызываем встроенную функцию dblquad, например, набираем в командном окне >> I = dblquad('f_podint ',-pi, pi, 0, 1) I = 23.0975

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , на отрезке
, на отрезке  .
.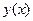 от каждого элемента вектора x.
от каждого элемента вектора x.








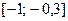 графики функций
графики функций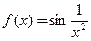 и
и  .
.





 на отрезке
на отрезке  в одном графическом окне и разных осях.
в одном графическом окне и разных осях.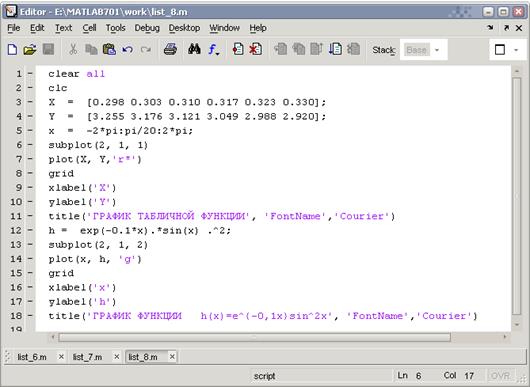


 .
. в узлах сетки.
в узлах сетки.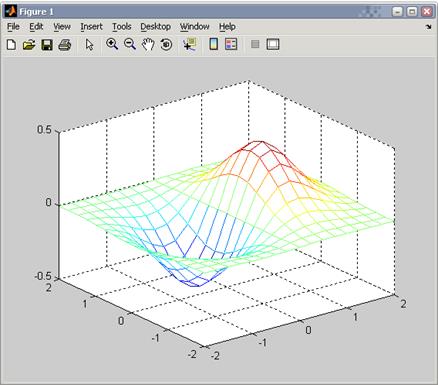

 .
.
 .
.
 .
.
 задана таблицей своих значений в точках
задана таблицей своих значений в точках  , (
, (  – четное) с постоянным шагом
– четное) с постоянным шагом  :
:



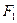

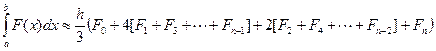 .
.
 , h – шаг таблицы.
, h – шаг таблицы. создадим таблицу, разделяя отрезок
создадим таблицу, разделяя отрезок  на 10 интервалов и для полученной табличной функции вычислим приближенное значение интеграла
на 10 интервалов и для полученной табличной функции вычислим приближенное значение интеграла  , используя функцию f_simps.
, используя функцию f_simps.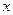 ;
; ;
; .
.