
|
|
Основы вычислений в MatLab.MATLAB 1. Command Window (Окно команд).
Математические выражения пишутся в командной строке после знака приглашения « >> ». Например, >> 1 + 2 Для выполнения действия нажмем клавишу «Enter». ans = >> | По умолчанию программа записывает результат в специальную переменную ans. Для сохранения результата под другим именем используют имя переменной и знак присваивания « = », например >> z = 1.25 /3.11 z = 0.40193 Редактировать в Command Window можно только текущую командную строку. Для того чтобы отредактировать ранее введенную команду, необходимо установить курсор в строку ввода и воспользоваться клавишами « Если команда заканчивается «;», то результат её действия не отображается в командной строке. Командное окно можно закрыть кнопкой « Главное Меню → Desktop → Desktop Layout → Default. Очистить командное окно можно с помощью меню: Главное Меню → Edit → Clear Command Window.
Главное меню системы MatLab. Главное меню MatLab содержит следующие пункты: File (Файл) – работа с файлами; Edit (Правка) – редактирование; View (Вид) – управление окнами; Web – связь с фирмой – разработчиком через Интернет; Window (Окно) – связь с окнами системы; Help (Справка) – связь со справочной системойMatLab.
Панель инструментов системы MATLAB. Кнопки панели инструментов имеют следующие назначения: New file (Создать) – выводит окна редакторов файлов; Open file (Открыть) – открывает окна загрузки файлов; Cut (Вырезать) – вырезает выделенный фрагмент и помещает в буфер обмена; Copy (Копировать) – копирует выделенный фрагмент в буфера обмена; Paste (Вставить) – переносит выделенный фрагмент из буфера обмена в строку ввода; Undo (Отменить) – отменяет результата предыдущей операции; Redo (Повторить) – повторяет результат предыдущей операции; Simulink – создает модель Simulink (расширения MatLab); Help Window (Помощь) – открывает окна справки.
4. Формат вывода результата вычислений. При вводе вещественных чисел для отделения дробной части используется точка! >> s = 0.3467819 s = 0.3468 Результат вычислений выводится в формате short(краткая запись числа), который определяется по умолчанию. Можно поменять формат на long (длинная запись числа). >> format long >> s s = 0.34678190000000 В списке Numerical Format имеются форматы чисел short– краткая запись числа; long– длинная запись числа; short e– краткая запись числа в формате с плавающей точкой; long e– длинная запись числа в формате с плавающей точкой; short g– вторая форма краткой записи числа; long g– вторая форма длинной записи числа;
Формат отображения числовых данных можно установить в меню File(файл) пункт Preferences(предпочтения). Перейти на вкладку Command Window (окно команд). В опции Text display(отображение текста), в списке Numeric format(числовой формат) установить short g, в опции Numeric display(отображение чисел) установить compact. Эти форматы вывода соответствуют выводу чисел в универсальной форме из пяти значащих цифр и с подавлением пробела между строками.
Основы вычислений в MatLab.
Для выполнения простейших арифметических операций в MatLab применяются операторы: · сложение и вычитание +, – ; · умножение и деление *, / ; · возведение в степень ^ .
Некоторые специальные переменные: ans – результат последней операции без знака присваивания; eps – относительная погрешность при вычислениях с плавающей точкой; pi – число i или j – мнимая единица; Inf – бесконечность NaN – неопределенное значение.
Некоторые встроенные элементарные функции MatLab: exp(x) – экспонента числа x; log(x) – натуральный логарифм числа x; sqrt(x) – квадратный корень из числа x; abs(x) – модуль числа x; sin(x), cos(x), tan(x), cot(x) – синус, косинус, тангенс, котангенс числа x; asin(x), acos(x), atan(x), acot(x) – арксинус, арккосинус, арктангенс, арккотангенс числа x; sec(x), csc(x) – секанс, косеканс числа x; round(x) – округление числа x до ближайшего целого; mod(x,y) – остаток от целочисленного деления x на y с учетом знака; sign(x) – возвращение знака числа x.
Вычислим значение выражение
>> exp(–2.5)*log(11.3)^0.3 – sqrt((sin(2.45*pi)+cos(3.78*pi))/tan(3.3)) ans = –3.2105
Если оператор не удается разместить в одной строке, то возможно продолжение его ввода в следующей строке, если в конце первой строки указать знак продолжения «…», например, >> exp(–2.5)*log(11.3)^0.3 – ... sqrt((sin(2.45*pi)+cos(3.78*pi))/tan(3.3))
Функции для работы с комплексными числами: Ввод комплексного числа >> z = 3 + 4i z = 3.0000 + 4.0000i Функции abs(z), angle(z) возвращают модуль complex(a,b) конструирует комплексное число по его действительной и мнимой части: conj(z)возвращает комплексно-сопряженное число; imag(z), real(z) возвращает мнимую и действительную часть комплексного числа z.
6. Векторы.
Ввод, сложение, вычитание, умножение на число. Вектор в MatLab формируется с помощью оператора квадратные скобки [ ]. При этом элементы вектора-столбца разделяют точкой с запятой «;», а элементы вектора-строки разделяют пробелом « » или запятой « , ». Введем вектор-столбец >> x = [1.3; 5.4; 6.9] x = 1.3 5.4 6.9 Введем вектор-строку >> y = [7.1 3.5 8.2] y = 7.1 3.5 8.2 Для транспонирования вектора применяют апостроф «’ »: >> z = y’ z = 7.1 3.5 8.2 Для нахождения суммы и разности векторов используются знаки « + » и «– »: >> с = x + z c = 8.4 8.9 15.1 Умножение вектора на число осуществляется как справа, так и слева при помощи знака « * ». >> t = 3*x t = 3.9 16.2 20.7 Векторы могут быть аргументами встроенных функций, например, >> d = sin(c) d = 0.8546 0.50102 0.5712 Для обращения к элементам векторов используются скобки (), например, >> x_2 = x(2) x_2 = 5.4 Последний элемент вектора можно выбрать, набрав команду >> X_end = x(end) X_end = 6.9 Из нескольких векторов можно составить один, например >> r = [x’ y] r = 1.3 5.4 6.9 7.1 3.5 8.2
Символ двоеточие « : » используется для выделения нескольких элементов из вектора, например >> w = r(3:5) w = 6.9 7.1 3.5 Символ двоеточие « : » также позволяет заменять элементы вектора, например, >> r(3:5)= 0 r = 1.3 5.4 0 0 0 8.2
Символ « : » также можно использовать для построения вектора, каждый элемент которого отличается от предыдущего на постоянное число, т.е. шаг, например >> h = [1:0.2:2] h = 1 1.2 1.4 1.6 1.8 2 Шаг может быть отрицательным (в этом случае начальное число должно быть больше конечного). Шаг, равный единице, можно не указывать >> k = [1:5] k = 1 2 3 4 5
Основные функции для работы с векторами.
Если вызвать функцию min или max с двумя выходными аргументами [m, k] = min(x), то первой переменной присваивается значение минимального (максимального элемента), а второй переменной присваивается номер этого элемента.
7 Матрицы.
Различные способы ввода матрицы. 1. Матрицу можно вводить как вектор-столбец, состоящий из двух элементов, каждый из которых является вектор - строкой и отделяется точкой с запятой. Например, введем матрицу
>> A = [3 1 –1; 2 4 3 ] A = 3 1 –1 2 4 3
2. Матрицу можно вводить построчно, выполняя последовательность команд: >> A = [3 1 –1 «Enter» 2 4 3] «Enter» В результате получим ту же матрицу.
Доступ к элементам матрицы осуществляется при помощи двух индексов – номеров строки и столбца: >> A(2, 3) ans = Создание матриц специального вида. Функция
Выделение блоков и заполнение матрицы при помощи индексации. Символ двоеточие « : » используется для выделения блоков из матрицы. Представляется в следующих формах:
Например, создадим матрицу
Для этого применяем последовательность команд >> T = zeros(5); >> T(1, :) = 1; >> T(end, 3:end) = –1 T = 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 –1 –1 –1 Действиями с матрицами и элементами матриц. Транспонирование матрицы из действительных чисел осуществляется с помощью апострофа « ’ ». Сложение и вычитание матриц одного размера осуществляется при помощи знаков « + » и « – ». Для умножения согласованных матриц используется знак «*». Этот же знак используется для произведения матрицы на число. Возведение квадратной матрицы в целую степень производится с использованием оператора « ^ ».
Некоторые функции для работы с матрицами. Функция
Сравнение матриц. Операторы отношения производят поэлементное сравнение двух матриц и возвращают матрицу той же размерности с элементами 1, где отношение истинно и 0, где отношение ложно:
< – меньше чем ( <= означает "меньше или равно"); > – больше чем ( >= означает "больше или равно").

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 » или«
» или«  ».
». », а кнопка « » служит для отделения окна от интерфейса системы. Вернуться к стандартной форме окна можно с помощью меню:
», а кнопка « » служит для отделения окна от интерфейса системы. Вернуться к стандартной форме окна можно с помощью меню: ;
; ;
;
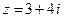
 и аргумент
и аргумент  комплексного числа
комплексного числа  , где
, где  ,
,  ;
; .
. .
.
 ;
; ;
;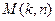 ,
,  ,
, 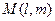 ,
,  ;
;  .
.