
|
|
Порядок аппроксимирующей функции12
Таблица 2.1.3 Таблица «невязок»
Решение задачи линейного программирования средствами MatLab Задача поиска условного экстремума функции многих переменных часто встречаются в экономических расчётах для минимизации затрат, максимализации прибыли и т. п. При этом экономическая задача описывается системами линейных уравнений и неравенств и относится к задачам линейного программирования. Типичным примером является так называемая задача производственного планирования, которая решает проблему оптимального выпуска товаров, дающего максимально возможный доход. Пример. Рассмотрим производство столов и стульев. Сведения о затратах ресурсов на единицу продукции, их наличии и о доходе от производимой продукции отражены в таблице 2.2.1.
Таблица 2.2.1. Затраты ресурсов
Доход (обозначим его символом
Для решения задач линейного программирования в MatLab используется функция linprog, которая ищет минимум для целевой функции Простейшие две формы обращения к ней состоят в следующем: x = linprog(f,A,b), x = linprog(f,A,b,Aeq,beq,lb,ub), [x,fv] = linprog(f,A,b,Aeq,beq,lb,ub), где f − вектор коэффициентов целевой функции − для нашего примера f=[10; 20]; A − матрица коэффициентов системы линейных неравенств A*x b − вектор свободных членов системы линейных неравенств A*x Aeq − матрица коэффициентов системы линейных равенств Aeq*x=beq − для нашего примера её нет (ставят пару пустых прямоугольных скобок []); beq − вектор свободных членов системы линейных равенств A*x=b − для нашего примера её нет (ставят пару пустых прямоугольных скобок []); lb и ub − вектора той же размерности, что и вектор x − ограничения на координаты lb x − искомый вектор оптимальных значений параметров; fv − значение целевой функции при оптимальном векторе параметров. Командное окно для решения нашей задачи имеет вид >> f=[10; 20]; >> A=[5 25;0.5 0;100 250;10 10]; >> b=[500; 15; 7500; 400]; >> lb=[0; 0]; >> [x,fv]=linprog(-f,A,b,[],[],lb) Optimization terminated. x = 25.0000 15.0000 fv = -550.0000 >> Так как функция linprog находит минимум, а нам необходимо найти максимум, то перед символом f в вызове функции поставлен знак минус. Таким образом, оптимальнее всего изготовить 25 стульев и 15 столов, при этом доход составит 550 руб. Задание.В соответствии с заданным вариантом (см. таблицу 2.2.2) найти оптимальное решение задачи производственного планирования.
Таблица 2.2.2 Варианты заданий 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 ), очевидно, равен
), очевидно, равен  , где
, где 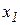 и
и 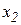 − искомые (вместе с
− искомые (вместе с  при наличии следующих ограничений:
при наличии следующих ограничений: ,
, ,
, ,
, ,
, .
. при наличии ограничений
при наличии ограничений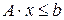 ,
, ,
, .
. b − для нашего примера A=[5 25;0.5 0;100 250;10 10];
b − для нашего примера A=[5 25;0.5 0;100 250;10 10];