|
Аппроксимация таблично заданной функции одной переменной методом наименьших квадратов
ОГЛАВЛЕНИЕ
Стр.
Предисловие 3
1. Задания к лабораторным работам 3
1.1. Варианты заданий к лабораторной работе № 1 3
1.2. Варианты заданий к лабораторной работе № 2 8
1.3. Варианты заданий к лабораторной работе № 3 12
1.4. Варианты заданий к лабораторной работе № 4 15
2. Расчётно-графические задания 19
2.1. Аппроксимация таблично заданной функции одной
переменной методом наименьших квадратов
2.2. Решение задачи линейного программирования
средствами MatLab
Отчётность по расчётно-графическому заданию
Литература
Предисловие
Настоящая методическая разработка состоит из двух независимых разделов:
- сборника вариантов заданий к лабораторным работам №№ 1-4;
- методических указаний к расчётно-графическим заданиям.
Первый раздел необходимо использовать совместно с работой Унру Н.Э. Информатика. Часть II. Методические указания к лабораторным работам для студентов 2 курса факультета РЭФ, обучающихся по специальностям "Радиотехника" и “Радиосвязь, радиовещание и телевидение”. – Новосибирск, НГТУ, 2009. – 59 с. Второй раздел − самодостаточный.
1. Задания к лабораторным работам
1.1. Варианты заданий к лабораторная работа № 1
Таблица 1.1.1
Системы линейных алгебраических уравнений
| N
вар.
| Система
уравнений
| N
вар.
| Система
уравнений
| |
|  
|
| 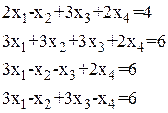
| |
| 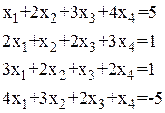
|
| 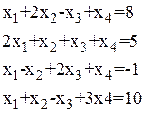
| |
| 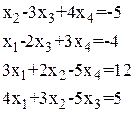
|
a
| 
| |
| 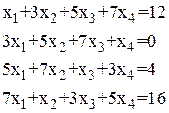
|
b
| 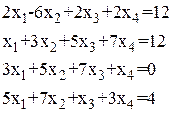
| |
| 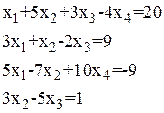
|
c
| 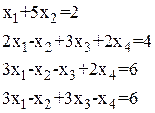
| |
| 
|
d
| 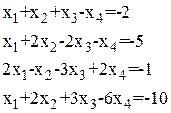
| |
| 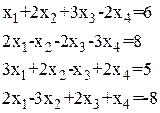
|
e
| 
| |
| 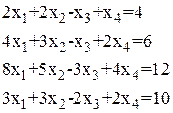
|
f
| 
|
Таблица 1.1.2
Нелинейные уравнения
| N вар.
| Вид уравнения 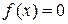
| a
| b
| |
| 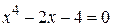
| -5
| 
| |
| 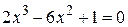
| - 
|
| |
| 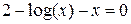
| 0.1
|
| |
| 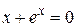
| -10
|
| |
| 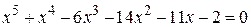
| -3
|
| |
| 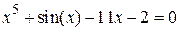
| - 
| 
| |
| 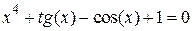
| -1.5
| 1.5
| |
| 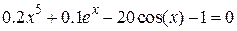
| -3
| 2.5
| |
| 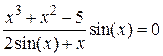
| -4
|
| |
| 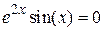
| -7
|
| | a
| 
|
|
| | b
| 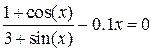
|
|
| | c
| 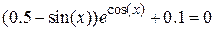
|
|
| | d
| 
| -7
| -2
| | e
| 
| -5
|
| | f
| 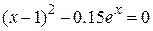
|
|
|
Варианты заданий к лабораторная работа № 2
Таблица 1.2.1
Аналитические выражения
| N вар.
| Исходные данные
| |
| 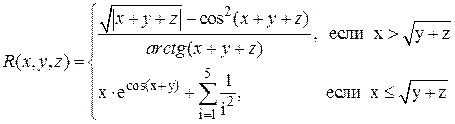
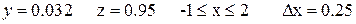
| |
| 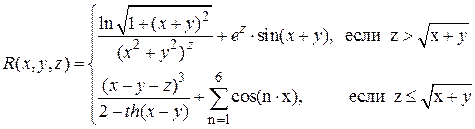
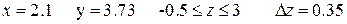
| |
| 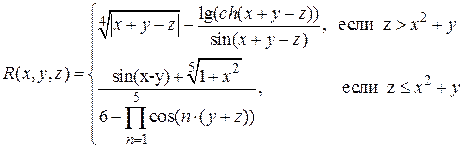
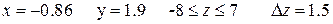
| |
| 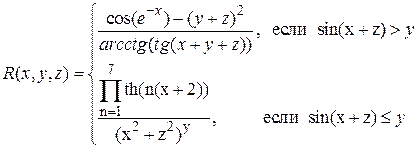
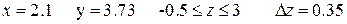
| |
| 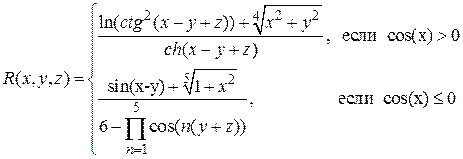
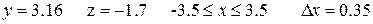
| |
| 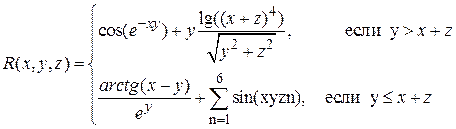
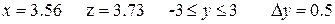
| |
| 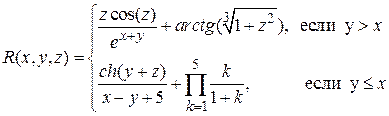
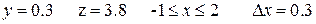
| |
| 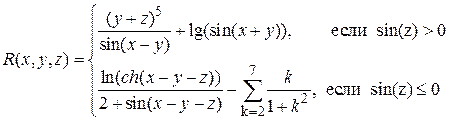

| |
| 
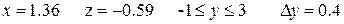
| |
| 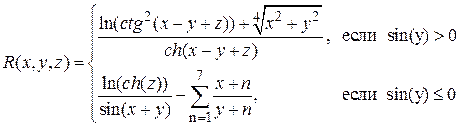
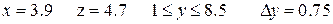
| | a
| 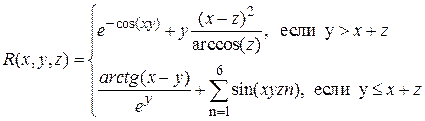
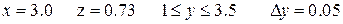
| | b
| 
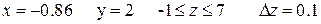
| | c
| 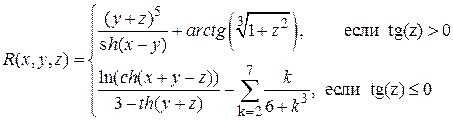
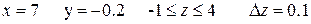
| | d
| 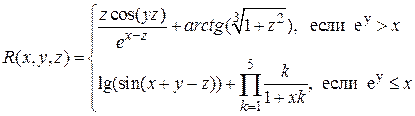
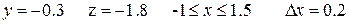
| | e
|  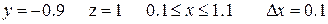
| | f
| 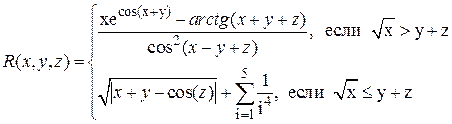
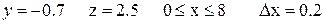
|
Таблица 1.2.2
Варианты функции f(x)
Варианты заданий к лабораторная работа № 3
Таблица 1.3.1
Исходные данные и тип интерполяционного полинома
Для анализа нелинейной цепи
| N вар.
| Векторы значений
| Тип полинома
| E,
В
| R, Ом
| | напряжения
| тока
| |
| [0.2, 0.4, 0.5]-1
| [0, 0.01, 0.04]-1
| степенной
|
|
| |
| [0.35, 0.5]-1
| [0.04, 0.6]-1
| экспоненциальный
|
|
| |
| [0.4, 0.6, 0.8]-1
| [0.002, 0.007, 0.017]-1
| степенной
|
|
| |
| [0.5, 0.7]-1
| [0.01, 0.5]-1
| экспоненциальный
|
|
| |
| [0.2, 0.4, 0.6]-1
| [0.0, 0.1, 0.26]-1
| степенной
|
|
| |
| [0.4, 0.6]-1
| [0.02, 0.065]-1
| экспоненциальный
|
|
| |
| [0.4, 0.6, 0.8]-1
| [0.02, 0.06, 0.14]-1
| степенной
|
|
| |
| [0.4, 0.8]-1
| [0.01, 0.06]-1
| экспоненциальный
| 1.5
|
| |
| [0.3, 0.4, 0.5]-1
| [0.003, 0.01, 0.04]-1
| степенной
|
|
| |
| [0.2, 0.5]-1
| [0.0005, 0.005]-1
| экспоненциальный
|
|
| | a
| [0.4, 0.5, 0.6]-1
| [0.02, 0.04, 0.065]-1
| степенной
|
|
| | b
| [0.2, 0.5]-1
| [0.01, 0.04]-1
| экспоненциальный
|
|
| | c
| [0.1, 0.5, 0.7]-1
| [0.04, 0.6, 1]-1
| степенной
|
|
| | d
| [0.4, 0.8]-1
| [0.002, 0.017]-1
| экспоненциальный
|
|
| | e
| [0.5, 0.6, 0.7]-1
| [0.01, 0.1, 0.5]-1
| степенной
|
|
| | f
| [0.2, 0.6]-1
| [0.01, 0.26]-1
| экспоненциальный
|
|
|
Таблица 1.3.2
Условия задачи Коши для дифференциального уравнения 1-го порядка
| N вар.
| y’=f(x,y), y(x0)=y0
| N вар.
| y’=f(x,y), y(x0)=y0
| |
| y’=y2+x2, y(0)=0.5
|
| y’=y-x, y(0)=1
| |
| y’=cos(x+y), y(0)=0
|
| y’=1+x-y2, y(0)=1
| |
| y’=e-y+x2, y(1)=0
| a
| y’=x3+y2, y(0)=0.5
| |
| y’=x ln(y), y(1)=1
| b
| y’=2.x+cos(y), y(0)=0
| |
| y’=x.y+8, y(0)=0
| c
| y’=ex-y2, y(0)=0
| |
| 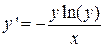 , y(1)=e , y(1)=e
| d
| 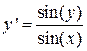 , , 
| |
|  , y(0)=1 , y(0)=1
| e
| 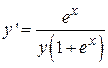 , y(0)=1 , y(0)=1
| |
| 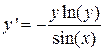 , , 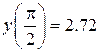
| f
| 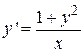 , , 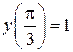
|
Таблица 1.3.3
Условия задачи Коши для системы
Дифференциальных уравнений 1-го порядка
| N вар.
| f1(x,y1,y2)
| f2(x,y1,y2)
| y1(a)
| y2(a)
| a
| b
| |
| 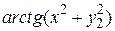
| 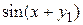
| 0.5
| 1.5
|
|
| |
| 
| 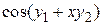
| -1
|
|
|
| |
| 
| 
|
|
|
|
| |
| 
| 
| -0.6
|
|
|
| |
| 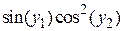
| 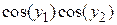
|
|
| -1
|
| |
| 
| 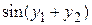
|
|
|
|
| |
| 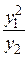
| 
|
|
|
|
| |
| 
| 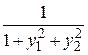
|
|
|
|
| |
| 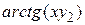
| 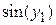
|
|
| -2
|
| |
| 
| 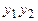
| -1
|
|
|
| | a
| 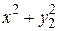
| 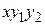
|
|
|
|
| | b
| 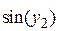
| 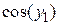
| 0.5
| -0.5
| -1
|
| | c
| 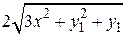
| 
| 0.5
| 1.2
|
|
| | d
| 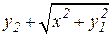
| 
| 0.8
| 3.5
|
|
| | e
| 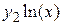
| 
| -2
| -1
|
|
| | f
| 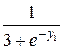
| 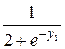
|
| -3
|
|
|
Таблица 1.3.4
Вид входных сигналов и параметры схемы при анализе переходных
Процессов
Вид 
| Параметры
| Вид 
| Параметры
| Вариант 0
 
    10 10
 3 3
  0 t
0 0 t
0   Т Т
|  =10 мкс =10 мкс
 =20 мкс
Т=30 мкс
R=50 Ом
L=0,1 мГн
C=12 нФ =20 мкс
Т=30 мкс
R=50 Ом
L=0,1 мГн
C=12 нФ
| Вариант 8
    2 2
 0 t 0 t
  T T
  -2 -2
|  =1 мс =1 мс
 =2 мс
Т=3,5 мс
R=200 Ом
L=20 мГн
C=800 нФ =2 мс
Т=3,5 мс
R=200 Ом
L=20 мГн
C=800 нФ
| Вариант 1
 
   5
0 5
0  t
0 t
0   T T
|  =5 мс =5 мс
 =20 мс
Т=40 мс
R=150 Ом
L=0,2 Гн
C=20 мкФ =20 мс
Т=40 мс
R=150 Ом
L=0,2 Гн
C=20 мкФ
| Вариант 9
   5 5
 0 t
0 0 t
0   T T
|  =5 мс =5 мс
 =20 мс
Т=40 мс
R=150 Ом
L=0,2 Гн
C=20 мкФ =20 мс
Т=40 мс
R=150 Ом
L=0,2 Гн
C=20 мкФ
| Вариант 2
 
  20 20
   7 7
  0 t
0 0 t
0   Т Т
|  =6 нс =6 нс
 =15 нс
Т=35 нс
R=1 кОм
L=1 мкГн
C=3 пФ =15 нс
Т=35 нс
R=1 кОм
L=1 мкГн
C=3 пФ
| Вариант a
  0
0    t t
  T
-15 T
-15
 
|  =100 нс =100 нс
 =200 нс
Т=650 нс
R=5 Ом
L=600 нГн
C=12 нФ =200 нс
Т=650 нс
R=5 Ом
L=600 нГн
C=12 нФ
| Вариант 3
 
   0 t 0 t
 -5 -5   Т Т
-20

|  =6 нс =6 нс
 =15 нс
Т=40 нс
R=150 Ом
L=1 мкГн
C=30 пФ =15 нс
Т=40 нс
R=150 Ом
L=1 мкГн
C=30 пФ
| Вариант b
   0 t 0 t
  -25 -25   T T

 -50 -50
|  =0,1 мс =0,1 мс
 =0,2 мс
Т=0,35 мс
R=20 Ом
L=0,4 мГн
C=400 нФ =0,2 мс
Т=0,35 мс
R=20 Ом
L=0,4 мГн
C=400 нФ
| Вариант 4
 
   20 20
  0 t
0 0 t
0   Т Т
|  =15 мкс =15 мкс
 =20 мкс
Т=50 мкс
R=25 Ом
L=80 мкГн
C=100 нФ =20 мкс
Т=50 мкс
R=25 Ом
L=80 мкГн
C=100 нФ
| Вариант c
  1
1
   0 t 0 t
  T T
 -25 -25
|  =15 мкс =15 мкс
 =40 мкс
Т=250 мкс
R=250 Ом
L=9 мГн
C=100 нФ =40 мкс
Т=250 мкс
R=250 Ом
L=9 мГн
C=100 нФ
| Вариант 5
 
 20 20

  7 7
  0 t
0 0 t
0   Т Т
|  =6 нс =6 нс
 =15 нс
Т=35 нс
R=1 кОм
L=1 мкГн
C=3 пФ =15 нс
Т=35 нс
R=1 кОм
L=1 мкГн
C=3 пФ
| Вариант d
  2
2     t t
  T
-15 T
-15
 
|  =100 нс =100 нс
 =200 нс
Т=650 нс
R=5 Ом
L=600 нГн
C=12 нФ =200 нс
Т=650 нс
R=5 Ом
L=600 нГн
C=12 нФ
| Вариант 6
 
   0 t
-5 0 t
-5   Т Т
 -20
-20

|  =6 нс =6 нс
 =15 нс
Т=40 нс
R=150 Ом
L=1 мкГн
C=30 пФ =15 нс
Т=40 нс
R=150 Ом
L=1 мкГн
C=30 пФ
| Вариант e
   0 t 0 t
  -25 -25   T T
 -50 -50
|  =0,1 мс =0,1 мс
 =0,2 мс
Т=0,35 мс
R=20 Ом
L=0,4 мГн
C=400 нФ =0,2 мс
Т=0,35 мс
R=20 Ом
L=0,4 мГн
C=400 нФ
| Вариант 7
 
   20 20
   0 t
0 0 t
0   Т Т
|  =15 мкс =15 мкс
 =20 мкс
Т=50 мкс
R=25 Ом
L=80 мкГн
C=100 нФ =20 мкс
Т=50 мкс
R=25 Ом
L=80 мкГн
C=100 нФ
| Вариант f
  3
3
   0 t 0 t
  T T
 -25 -25
|  =15 мкс =15 мкс
 =40 мкс
Т=250 мкс
R=250 Ом
L=9 мГн
C=100 нФ =40 мкс
Т=250 мкс
R=250 Ом
L=9 мГн
C=100 нФ
|
Таблица 1.3.5
Вид входных сигналов и параметры схемы при анализе переходных
Процессов
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|




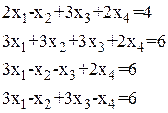
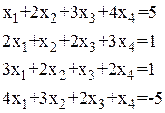
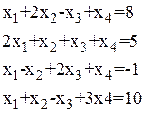
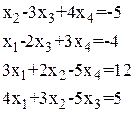

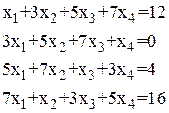
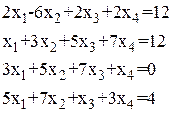
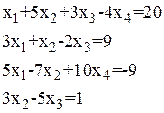
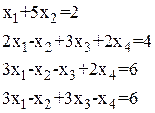

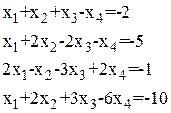
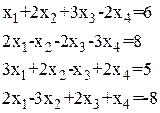

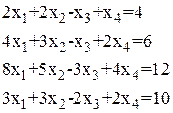

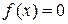
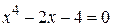

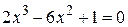
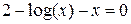
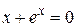
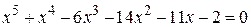
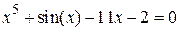
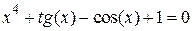
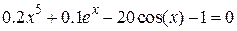
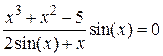
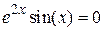

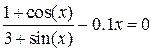
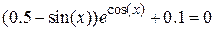


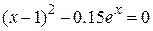
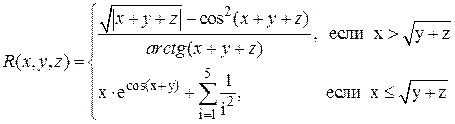
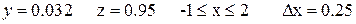
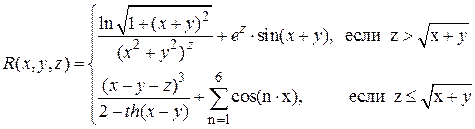
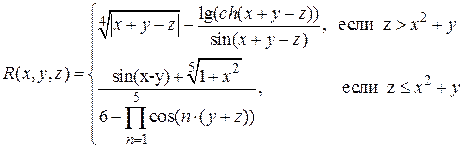
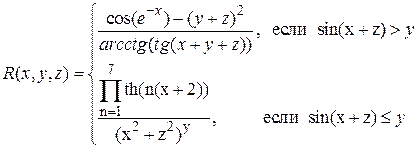
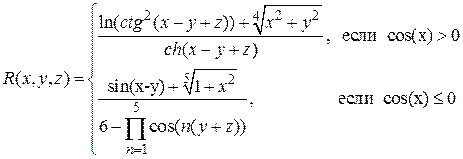
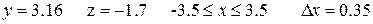
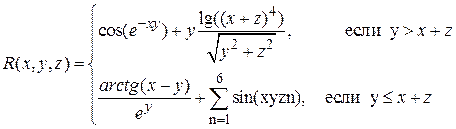
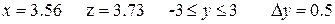
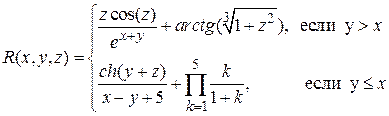
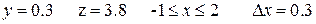
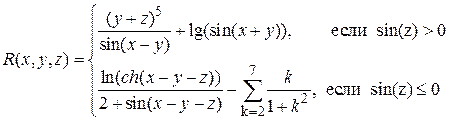


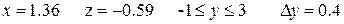
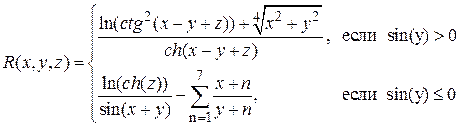
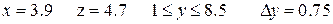
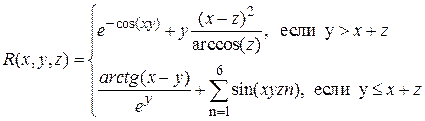
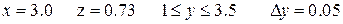

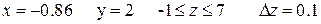
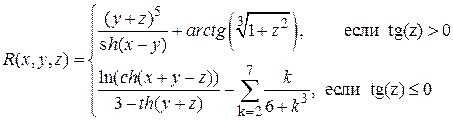
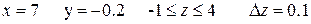
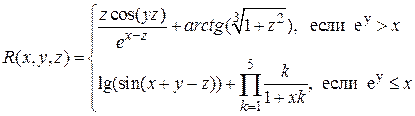
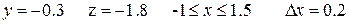

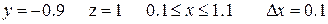
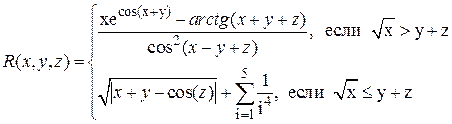
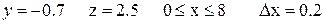





 -
-  -
- 




 -
- 





 1
1


 -1
-1






 -
-  -1
-1






 -
- 








 -
-  -
- 







 -
-  -
- 






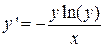 , y(1)=e
, y(1)=e
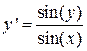 ,
, 
 , y(0)=1
, y(0)=1
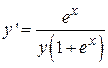 , y(0)=1
, y(0)=1
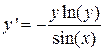 ,
, 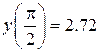
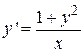 ,
, 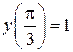
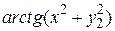
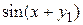

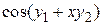




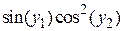
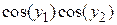

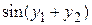
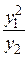


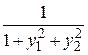
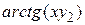
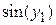

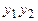
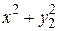
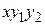
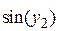
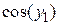
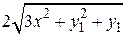

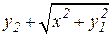

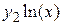

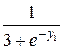
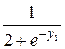




 10
10
 3
3

 0 t
0
0 t
0 
 Т
Т



 2
2
 0 t
0 t

 -2
-2





 0 t
0
0 t
0 

 20
20


 7
7

 0 t
0
0 t
0 


 t
t




 0 t
0 t




 0 t
0 t


 -50
-50


 20
20



 0 t
0 t -25
-25 20
20





 -20
-20



 -25
-25