
|
|
Возбуждение вихревых токов. Скин-эффект.Существование токов, которые замыкаются внутри электропроводящего объекта, было установлено Бернардом Леоном Фуко, обратившему внимание на нагревание металлических тел при быстром их вращении во внешнем магнитном поле, а физическая природа токов и причины их образования были выявлены Майклом Фарадеем, открывшим явление электромагнитной индукции. При размещении над поверхностью электропроводящего объекта плоской круговой катушки с переменным током, силовые линии создаваемого катушкой переменного магнитного поля будут пронизывать часть поверхности объекта. Изменение поля будет приводить к изменению магнитного потока, пронизывающего мысленно выделяемые на поверхности объекта контура, в которых, в соответствии с законом электромагнитной индукции, должны возникать индукционные токи. Поскольку, согласно правилу Ленца, эти токи должны быть направлены так, чтобы ослабить вызвавшее их поле, то контуры токов должны быть концентрическими окружностями (вихревые токи). Для вихревых токов характерна концентрация вблизи поверхности проводника (скин-эффект). Протекание вихревых токов вызывает нагрев металлических объектов и этот эффект часто используется в технике для термической обработки изделий, в том числе, для поверхностной закалки (см. 5.4). Применение вихревых токов для неразрушающего контроля известно с 1879 года, когда англичанин Хьюз для сравнения свойств металлических объектов использовал устройство с дифференциальным трансформаторным ВТП (см. далее п. 7), возбуждающие обмотки которого подключались к генератору переменного напряжения, а измерительные – к гальванометру. Широкое практическое применение вихретоковых методов контроля началось в сороковых годах нашего века. В настоящее время вихретоковые методы и приборы по распространенности и объемам контролируемой продукции занимают второе место после акустических методов. Переменный ток как источник электромагнитного поля. Для генерации вихревых токов необходим источник переменного (электромагнитного) поля, силовые линии которого должны пронизывать поверхность электропроводящего объекта. Простейшим источником электромагнитного поля является виток или катушка с переменным током. Сами вихревые токи тоже являются переменными. В измерительных катушках вихретоковых преобразователей также наводится переменная э. д. с. Таким образом, для понимания физических процессов и правильного применения вихретокового контроля необходимо учитывать законы цепей переменного тока. Под воздействием переменного напряжения ток в цепи изменяется во времени и, вообще говоря, в каждый момент ток оказывается не одинаковым на разных участках цепи (из-за того, что электромагнитные возмущения распространяются хотя и с очень большой, но конечной скоростью). Однако имеется много случаев, когда мгновенные значения тока оказываются практически одинаковыми на всех участках цепи (такой ток называется квазистационарным). Для этого все изменения во времени должны происходить настолько медленно, чтобы распространение электромагнитных возмущений можно было считать мгновенным. Если Например, для цепи длиной Далее будем предполагать, что условие квазистационарности выполняется, и токи будем считать квазистационарными. В этом случае можно использовать формулы, полученные в статических полях и, в частности, то, что мгновенные значения квазистационарных токов подчиняются закону Ома.
 и конденсатор емкости и конденсатор емкости  , могут возникнуть электрические колебания. Поэтому такую цепь называют колебательным контуром. Выясним, каким образом в колебательном контуре возникают и поддерживаются электрические колебания. , могут возникнуть электрические колебания. Поэтому такую цепь называют колебательным контуром. Выясним, каким образом в колебательном контуре возникают и поддерживаются электрические колебания.
Рис. 3.1. Колебательный контур
Пусть вначале верхняя обкладка конденсатора заряжена положительно, а нижняя отрицательно (рис.3.1а). При этом вся энергия колебательного контура сосредоточена в конденсаторе. Замкнем ключ В контуре при отсутствии сопротивления проводников будут совершаться строго периодические колебания. В ходе процесса периодически изменяются заряд на обкладках конденсатора, напряжение на нем и ток через катушку. Колебания сопровождаются взаимными превращениями энергии электрического и магнитного полей. Если имеется активное сопротивление проводников ( Необходимо получить уравнение колебаний в контуре, содержащем последовательно соединенные конденсатор Выберем направление положительного обхода контура, например, по часовой стрелке. Обозначим через
Следовательно, если Согласно закону Ома для участка цепи 1RL2 (рис. 3.1в)
где
или с учетом (3.1) можно записать
Выражение (3.4) – это уравнение колебательного контура. Найдя с помощью этого уравнения заряд как функцию времени Уравнению колебательного контура можно придать вид:
где введены следующие обозначения
Величину Свободные затухающие колебания. Каждый реальный контур обладает активным сопротивлением, и энергия, запасенная в контуре, постепенно расходуется на нагревание. Свободные колебания будут затухающими. Уравнение данного колебательного контура мы получим, положив в (3.5)
Можно показать, что при
где
а
где
Рис. 3.2. Затухающие колебания
1. Коэффициент затухания
2. Логарифмический декремент затухания
где
где Если затухание мало (
3. Добротность
где
При
Вынужденные установившиеся колебания.Вернемся к уравнениям колебательного контура (3.4) и (3.5) и рассмотрим случай, когда в контур включена внешняя переменная э. д. с.
Этот закон занимает особое положение благодаря свойствам самого колебательного контура сохранять гармонический вид колебаний при действии внешней гармонической э. д. с. В этом случае уравнение колебательного контура записывается как
или
Решение этого уравнения, как известно из математики, представляет собой сумму общего решения однородного уравнения (без правой части) и частного решения неоднородного уравнения. Нас будут интересовать только установившиеся колебания, т.е. частное решение этого уравнения (общее решение однородного уравнения экспоненциально затухает, и по прошествии некоторого времени оно практически исчезает, превращается в нуль). Нетрудно убедиться, что это решение имеет вид
где Чтобы определить постоянные Продифференцировав (3.24) по времени
Запишем это выражение так:
где
Наша задача найти
где слева записана сумма напряжений на индуктивности
Рис. 3.3. Векторная диаграмма
Из последних трех формул видно, что Из прямоугольного треугольника этой диаграммы легко получить следующие выражения для
Полученная векторная диаграмма оказывается весьма полезной при решении многих конкретных вопросов. Она позволяет наглядно, легко и быстро анализировать различные ситуации.
Рис. 3.4. Резонансные кривые силы тока
Графики зависимостей амплитуд тока
Максимум при резонансе оказывается тем выше и острее, чем меньше коэффициент затухания Аналогично можно получить резонансные кривые для заряда на конденсаторе Резонансные частоты для
Чем меньше коэффициент затухания Форма резонансных кривых определенным образом связана с добротностью
Таким образом, добротность контура (при Добротность контура связана и с другой важной характеристикой резонансной кривой – ее шириной. Оказывается, при
где Возбуждение сильных колебаний при частоте внешней э. д. с. или напряжения, равной или близкой к собственной частоте колебательного контура, т.е. резонанс, используют для выделения из сложного напряжения нужной составляющей. На этом основана вся техника радиоприема. Для того чтобы радиоприемник принимал интересующую нас радиостанцию, его необходимо настроить, т. е. изменением Переменный ток. Полное сопротивление (импеданс). Установившиеся вынужденные электрические колебания можно рассматривать как протекание в цепи, обладающей емкостью, индуктивностью и активным сопротивлением
ток в цепи изменяется по закону
где
Задача сводится к определению амплитуды силы тока и сдвига тока по фазе относительно Полученное выражение для амплитуды силы тока
Видно, что при
При этом величину
Заметим, что индуктивное сопротивление растет с увеличением частоты Реактивное сопротивление измеряют в тех же единицах, что и активное, однако только активное сопротивление определяет необратимые процессы в цепи, такие, например, как преобразование электромагнитной энергии в джоулеву теплоту. Скин-эффект. Вихревые токи в электропроводящих объектах возбуждают внешним переменным магнитным полем, создающим переменный магнитный поток, пронизывающий тело объекта. Амплитуда внешнего электромагнитного поля имеет максимальное значение вблизи поверхности и уменьшается по мере проникновения вглубь проводника[6]. Простейшим объяснением этого явления является то, что вихревые токи, наведенные в близких к поверхности (и к источнику переменного поля) слоях проводника, в соответствии с правилом Ленца своим полем ослабляют внешнее поле, а также рассеивают энергию поля за счет нагрева проводника. В нижележащие слои поле проникает ослабленным. Возбуждаемые в этих слоях вихревые токи в свою очередь продолжают процесс ослабления. Это явление называется скин-эффектом. Таким образом, вихревые токи оказываются сконцентрированными вблизи поверхности проводника в так называемом скин-слое. Вихревые токи протекают преимущественно под датчиком, в небольшом объеме изделия. Их амплитуда и фаза различны в каждой точке на поверхности изделия и в глубине. Если для создания электромагнитного поля использовать переменный синусоидальный ток и считать, что поле однородно, то уравнения Максвелла в этом случае для пластины или полупространства можно свести к дифференциальному уравнению:
где Общее решение для напряженности магнитного поля можно представить следующим образом:
где В проводящем полупространстве поле затухает по закону:
Таким образом, в этом случае мы имеем дело с плоской поперечной волной. Она характеризуется тем, что в любой плоскости, перпендикулярной распространению волны, ее фаза и амплитуда постоянны. Важнейшей вытекающей отсюда характеристикой является глубина проникновения волны
При Если волна падает на металл под некоторый углом, то величину составляющих волн будет характеризовать коэффициент преломления В контроле используется понятие глубины проникновения электромагнитного поля вихретокового преобразователя ( Изменение плотности вихревых токов, вызванных падающей на полупространство плоской электромагнитной волной, может быть описано выражением:
где Для глубины проникновения электромагнитного поля ВТП из (3.47) следует
Реальная глубина проникновения вихревых токов, индуцированных в плоском металлическом теле наложенной на его поверхность плоской катушкой с переменным током, всегда меньше теоретической. При контроле цилиндрических и сферических поверхностей в металле возникают цилиндрические и шаровые (поперечные) электромагнитные волны. В этом случае глубина проникновения вихревых токов будет несколько больше, чем в случае плоской волны. Расчет пространственного распределения электромагнитного поля и вихревых токов. Расчет проникновения электромагнитного поля и пространственного распределения вихревых токов в проводящих, а также в проводящих ферромагнитных средах является весьма нетривиальной задачей, требующей решения системы уравнений Максвелла при корректном выборе граничных условий и материальных уравнений. Во многих случаях для описания произвольного электромагнитного поля вместо силовых характеристик – напряженности электрического поля
Уравнения для потенциалов поля имеют более простую форму, чем исходные уравнения Максвелла, что упрощает задачу нахождения переменных электромагнитных полей. Существенное упрощение уравнений для потенциалов электромагнитного поля возможно благодаря тому, что потенциалы определяются неоднозначно. Если вместо
где
где
где Уравнения (3.54) и (3.55) позволяют определять потенциалы 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 - длина цепи, то на прохождение длины
- длина цепи, то на прохождение длины  электромагнитное возмущение затрачивает время порядка
электромагнитное возмущение затрачивает время порядка  . Для периодически изменяющихся токов условие квазистационарности будет выполнено, если
. Для периодически изменяющихся токов условие квазистационарности будет выполнено, если 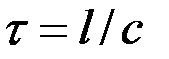 <<
<<  , где
, где  - период изменений.
- период изменений. = 3 м время прохождения волны составляет
= 3 м время прохождения волны составляет  = 10-8 с. Значит, токи можно считать квазистационарными вплоть до частот 106 Гц (это соответствует
= 10-8 с. Значит, токи можно считать квазистационарными вплоть до частот 106 Гц (это соответствует  = 10-6 с).
= 10-6 с). . Конденсатор начнет разряжаться, и через катушку
. Конденсатор начнет разряжаться, и через катушку  потечет ток. Электрическая энергия конденсатора начнет превращаться в магнитную энергию катушки. Этот процесс закончится, когда конденсатор полностью разрядится, а ток в цепи достигнет максимума (рис.3.1б). С этого момента ток, не меняя направления, начнет убывать. Однако он прекратится не сразу – его будет поддерживать э. д. с. самоиндукции. Ток будет перезаряжать конденсатор, возникнет электрическое поле, стремящееся ослабить ток. Наконец, ток прекратится, а заряд на конденсаторе достигнет максимума. С этого момента конденсатор начнет разряжаться опять, ток потечет в обратном направлении и т.д. – процесс будет повторяться.
потечет ток. Электрическая энергия конденсатора начнет превращаться в магнитную энергию катушки. Этот процесс закончится, когда конденсатор полностью разрядится, а ток в цепи достигнет максимума (рис.3.1б). С этого момента ток, не меняя направления, начнет убывать. Однако он прекратится не сразу – его будет поддерживать э. д. с. самоиндукции. Ток будет перезаряжать конденсатор, возникнет электрическое поле, стремящееся ослабить ток. Наконец, ток прекратится, а заряд на конденсаторе достигнет максимума. С этого момента конденсатор начнет разряжаться опять, ток потечет в обратном направлении и т.д. – процесс будет повторяться. ), то помимо описанного процесса будет происходить преобразование электромагнитной энергии в джоулеву теплоту.
), то помимо описанного процесса будет происходить преобразование электромагнитной энергии в джоулеву теплоту. , катушку индуктивности
, катушку индуктивности  , активное сопротивление
, активное сопротивление  и внешнюю переменную э. д. с.
и внешнюю переменную э. д. с.  (рис. 3.1в).
(рис. 3.1в). заряд той обкладки конденсатора, направление от которой к другой обкладке совпадает с выбранным положительным направлением обхода контура. Тогда ток в контуре определяется как
заряд той обкладки конденсатора, направление от которой к другой обкладке совпадает с выбранным положительным направлением обхода контура. Тогда ток в контуре определяется как . (3.1)
. (3.1) > 0, то и
> 0, то и  > 0, и наоборот (т.е. знак
> 0, и наоборот (т.е. знак  совпадает со знаком
совпадает со знаком  ).
). , (3.2)
, (3.2) - э. д. с. самоиндукции. В нашем случае
- э. д. с. самоиндукции. В нашем случае  и
и  (знак
(знак  должен совпадать со знаком разности
должен совпадать со знаком разности  , ибо
, ибо  ). Поэтому уравнение (3.2) можно переписать в виде
). Поэтому уравнение (3.2) можно переписать в виде (3.3)
(3.3) . (3.4)
. (3.4) , можно легко вычислить напряжение на конденсаторе как
, можно легко вычислить напряжение на конденсаторе как  и силу тока
и силу тока  по формуле (3.1).
по формуле (3.1). , (3.5)
, (3.5) ,
,  ,
,  . (3.6)
. (3.6) называют собственной частотой контура,
называют собственной частотой контура,  - коэффициентом затухания.
- коэффициентом затухания. . Тогда
. Тогда . (3.10)
. (3.10) <
<  решение этого однородного дифференциального уравнения имеет вид
решение этого однородного дифференциального уравнения имеет вид , (3.11)
, (3.11) , (3.12)
, (3.12) и
и  - постоянные, определяемые из начальных условий. График функции (3.11) показан на рис. 3.2. Эта функция определяет затухающие колебания. Чем больше величина
- постоянные, определяемые из начальных условий. График функции (3.11) показан на рис. 3.2. Эта функция определяет затухающие колебания. Чем больше величина  (коэффициент затухания), тем больше скорость уменьшения амплитуды колебаний. Хотя функция (3.11) не периодическая, тем не менее, величину
(коэффициент затухания), тем больше скорость уменьшения амплитуды колебаний. Хотя функция (3.11) не периодическая, тем не менее, величину  называют, периодом затухающих колебаний:
называют, периодом затухающих колебаний: , (3.13)
, (3.13) - период свободных незатухающих колебаний. Множитель
- период свободных незатухающих колебаний. Множитель  в (3.11) называют амплитудой затухающих колебаний. Зависимость ее от времени показана пунктиром на рис. 3.2. Можно указать следующие характеристики затухания.
в (3.11) называют амплитудой затухающих колебаний. Зависимость ее от времени показана пунктиром на рис. 3.2. Можно указать следующие характеристики затухания. и время релаксации
и время релаксации  - время, за которое амплитуда колебаний уменьшается в
- время, за которое амплитуда колебаний уменьшается в  раз. Из формулы (3.11) нетрудно видеть, что
раз. Из формулы (3.11) нетрудно видеть, что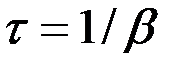 . (3.14)
. (3.14) . Он определяется как натуральный логарифм отношения двух значений амплитуд, взятых через период колебания
. Он определяется как натуральный логарифм отношения двух значений амплитуд, взятых через период колебания  :
: , (3.15)
, (3.15) - амплитуда соответствующей величины (
- амплитуда соответствующей величины (  ,
,  ,
,  ). Или, как следует из формул (3.14) и (3.15):
). Или, как следует из формул (3.14) и (3.15): , (3.16)
, (3.16) - число колебаний за время
- число колебаний за время  , т.е. за время, в течение которого амплитуда колебаний уменьшается в
, т.е. за время, в течение которого амплитуда колебаний уменьшается в  раз.
раз. <
<  ), то
), то  и согласно (3.15)
и согласно (3.15) . (3.17)
. (3.17) колебательного контура. По определению
колебательного контура. По определению , (3.18)
, (3.18) - логарифмический декремент затухания. Чем меньше затухание, тем больше
- логарифмический декремент затухания. Чем меньше затухание, тем больше  . При слабом затухании (
. При слабом затухании (  <
<  ) согласно (3.17) добротность
) согласно (3.17) добротность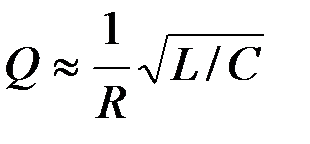 . (3.19)
. (3.19) вместо колебаний будет происходить апериодический разряд конденсатора. Активное сопротивление контура, при котором наступает апериодический процесс, называют критическим:
вместо колебаний будет происходить апериодический разряд конденсатора. Активное сопротивление контура, при котором наступает апериодический процесс, называют критическим: . (3.20)
. (3.20) , зависящая от времени по гармоническому закону:
, зависящая от времени по гармоническому закону: . (3.21)
. (3.21) (3.22)
(3.22) . (3.23)
. (3.23) , (3.24)
, (3.24) - амплитуда заряда на конденсаторе;
- амплитуда заряда на конденсаторе;  - разность фаз между колебаниями заряда и внешней э. д. с.
- разность фаз между колебаниями заряда и внешней э. д. с.  (3.21). Как мы видим,
(3.21). Как мы видим,  и
и  определяются только свойствами самого контура и вынуждающей э. д. с.
определяются только свойствами самого контура и вынуждающей э. д. с.  , причем оказывается, что
, причем оказывается, что  > 0, поэтому
> 0, поэтому  всегда отстает по фазе от
всегда отстает по фазе от  .
. и
и  , надо подставить (3.24) в исходное уравнение (3.23) и преобразовать полученное выражение. Проще, однако, сначала найти ток
, надо подставить (3.24) в исходное уравнение (3.23) и преобразовать полученное выражение. Проще, однако, сначала найти ток  и затем его выражение подставить в исходное уравнение (3.22). Попутно будет решен и вопрос с постоянными
и затем его выражение подставить в исходное уравнение (3.22). Попутно будет решен и вопрос с постоянными  и
и  .
. , найдем
, найдем .
. , (3.25)
, (3.25) - амплитуда тока;
- амплитуда тока;  - сдвиг по фазе между током и внешней э. д. с.
- сдвиг по фазе между током и внешней э. д. с.  ,
, ,
,  . (3.26)
. (3.26) и
и  . С этой целью мы поступим следующим образом. Представим исходное уравнение (3.22) в виде
. С этой целью мы поступим следующим образом. Представим исходное уравнение (3.22) в виде , (3.27)
, (3.27) , сопротивлении
, сопротивлении  и емкости
и емкости  . Таким образом, мы видим, что сумма этих напряжений равна в каждый момент внешней э. д. с.
. Таким образом, мы видим, что сумма этих напряжений равна в каждый момент внешней э. д. с.  . Учитывая соотношения (3.26), запишем:
. Учитывая соотношения (3.26), запишем: , (3.28)
, (3.28) , (3.29)
, (3.29) . (3.30)
. (3.30)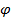


 находится в фазе с током
находится в фазе с током  ,
,  отстает по фазе от тока
отстает по фазе от тока  на
на  , а
, а  опережает
опережает  на
на  . Все это можно наглядно представить с помощью векторной диаграммы (рис. 3.3), изобразив амплитуды напряжений
. Все это можно наглядно представить с помощью векторной диаграммы (рис. 3.3), изобразив амплитуды напряжений  ,
,  ,
,  и их векторную сумму, равную согласно (3.27) вектору величины
и их векторную сумму, равную согласно (3.27) вектору величины  .
.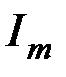 и
и  :
: , (3.31)
, (3.31) . (3.32)
. (3.32) , заряда
, заряда  на конденсаторе и напряжений
на конденсаторе и напряжений  ,
,  и
и  от частоты
от частоты  внешней э. д. с.
внешней э. д. с.  называют резонансными кривыми. Резонансные кривые для силы тока
называют резонансными кривыми. Резонансные кривые для силы тока 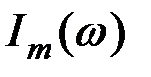 показаны на рис. 3.4. Как видно из выражения (3.31), амплитуда силы тока имеет максимальное значение при
показаны на рис. 3.4. Как видно из выражения (3.31), амплитуда силы тока имеет максимальное значение при  . Следовательно, резонансная частота для силы тока совпадает с собственной частотой контура:
. Следовательно, резонансная частота для силы тока совпадает с собственной частотой контура: . (3.33)
. (3.33) .
. , для напряжения
, для напряжения  на конденсаторе и т.д.
на конденсаторе и т.д. ,
,  и
и  определяются следующими формулами:
определяются следующими формулами: ,
, , (3.34)
, (3.34) .
. , тем ближе резонансные частоты всех величин к значению
, тем ближе резонансные частоты всех величин к значению  .
. контура. Особенно простой эта связь оказывается для случая слабого затухания, т. е. при
контура. Особенно простой эта связь оказывается для случая слабого затухания, т. е. при  <<
<<  . В этом случае
. В этом случае . (3.35)
. (3.35) <<
<<  ) показывает, во сколько раз максимальное значение амплитуды напряжения на конденсаторе (и на индуктивности) превышает амплитуду внешней э. д. с.
) показывает, во сколько раз максимальное значение амплитуды напряжения на конденсаторе (и на индуктивности) превышает амплитуду внешней э. д. с. <<
<< 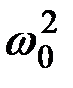
 , (3.36)
, (3.36) - резонансная частота,
- резонансная частота,  - ширина резонансной кривой на «высоте», равной 0,7 от максимальной, т. е. в резонансе.
- ширина резонансной кривой на «высоте», равной 0,7 от максимальной, т. е. в резонансе. и
и  колебательного контура добиться совпадения его собственной частоты с частотой электромагнитных волн, излучаемых радиостанцией. Это же явление используется в вихретоковом контроле для построения высокочувствительных схем измерения, когда сам объект контроля делают элементом резонансного контура.
колебательного контура добиться совпадения его собственной частоты с частотой электромагнитных волн, излучаемых радиостанцией. Это же явление используется в вихретоковом контроле для построения высокочувствительных схем измерения, когда сам объект контроля делают элементом резонансного контура. , переменного тока. Под действием внешнего напряжения (оно играет роль внешней э. д. с.
, переменного тока. Под действием внешнего напряжения (оно играет роль внешней э. д. с. 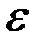 )
) (3.37)
(3.37) , (3.38)
, (3.38) ,
,  . (3.39)
. (3.39) .
. можно рассматривать как закон Ома для амплитудных значений тока и напряжения. Стоящую в знаменателе этого выражения величину, имеющую размерность сопротивления, обозначают буквой
можно рассматривать как закон Ома для амплитудных значений тока и напряжения. Стоящую в знаменателе этого выражения величину, имеющую размерность сопротивления, обозначают буквой  и называют полным сопротивлением или импедансом:
и называют полным сопротивлением или импедансом: . (3.40)
. (3.40) это сопротивление минимально и равно активному сопротивлению
это сопротивление минимально и равно активному сопротивлению  . Величину, стоящую в круглых скобках формулы (3.40), обозначают
. Величину, стоящую в круглых скобках формулы (3.40), обозначают  и называют реактивным сопротивлением:
и называют реактивным сопротивлением: . (3.41)
. (3.41) называют индуктивным сопротивлением, а величину
называют индуктивным сопротивлением, а величину  - емкостным сопротивлением. Их обозначают соответственно
- емкостным сопротивлением. Их обозначают соответственно  и
и  . Итак,
. Итак, ,
,  ,
,  ,
, 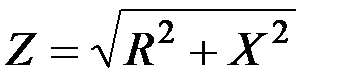 . (3.42)
. (3.42) , а емкостное – уменьшается. Когда говорят, что в цепи отсутствует емкость, то это надо понимать в смысле отсутствия емкостного сопротивления, которое равно
, а емкостное – уменьшается. Когда говорят, что в цепи отсутствует емкость, то это надо понимать в смысле отсутствия емкостного сопротивления, которое равно 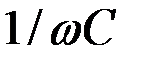 и, следовательно, обращается в нуль, если
и, следовательно, обращается в нуль, если  (при замене конденсатора закороченным участком).
(при замене конденсатора закороченным участком). , (3.43)
, (3.43) – расстояние от поверхности до слоя в объекте контроля, в котором рассчитывается поле
– расстояние от поверхности до слоя в объекте контроля, в котором рассчитывается поле  ;
;  – мнимая единица;
– мнимая единица;  – круговая частота тока возбуждения;
– круговая частота тока возбуждения;  и
и  – удельная электрическая проводимость и магнитная проницаемость материала объекта контроля соответственно.
– удельная электрическая проводимость и магнитная проницаемость материала объекта контроля соответственно. , (3.44)
, (3.44) – постоянная вихревых токов (вихретоковый параметр). В выражении (3.44) напряженность поля
– постоянная вихревых токов (вихретоковый параметр). В выражении (3.44) напряженность поля  представляется в виде двух волн: падающей (первое слагаемое) и отраженной от нижней поверхности пластины (второе слагаемое).
представляется в виде двух волн: падающей (первое слагаемое) и отраженной от нижней поверхности пластины (второе слагаемое). . (3.45)
. (3.45) , то есть такое расстояние от поверхности полупространства, на котором амплитуда падающей волны c частотой
, то есть такое расстояние от поверхности полупространства, на котором амплитуда падающей волны c частотой  уменьшается в
уменьшается в  раз:
раз: . (3.46)
. (3.46) фаза волны изменится на 180°. Это расстояние называется длиной электромагнитной волны в металле.
фаза волны изменится на 180°. Это расстояние называется длиной электромагнитной волны в металле. . В диапазоне частот, используемых в вихретоковом контроле, значение коэффициента преломления весьма велико. Это означает, что плоская электромагнитная волна, падая на границу раздела воздуха и металла даже под малый углом, будет входить в металл по нормали к его поверхности. Это условие сохраняется и для криволинейной поверхности при большом радиусе ее кривизны.
. В диапазоне частот, используемых в вихретоковом контроле, значение коэффициента преломления весьма велико. Это означает, что плоская электромагнитная волна, падая на границу раздела воздуха и металла даже под малый углом, будет входить в металл по нормали к его поверхности. Это условие сохраняется и для криволинейной поверхности при большом радиусе ее кривизны. ), за которую принимают расстояние от поверхности объекта контроля до слоя, в котором плотность вихревых токов в
), за которую принимают расстояние от поверхности объекта контроля до слоя, в котором плотность вихревых токов в  раз меньше, чем на поверхности.
раз меньше, чем на поверхности. , (3.47)
, (3.47) - глубина;
- глубина;  и
и  - плотность вихревых токов на глубине
- плотность вихревых токов на глубине  - линейная частота электромагнитного поля (т.е. тока в катушке);
- линейная частота электромагнитного поля (т.е. тока в катушке);  и
и  - магнитная проницаемость и удельная электрическая проводимость материала полупространства соответственно.
- магнитная проницаемость и удельная электрическая проводимость материала полупространства соответственно. . (3.48)
. (3.48) и магнитной индукции
и магнитной индукции  - целесообразно использовать две другие величины: векторный потенциал
- целесообразно использовать две другие величины: векторный потенциал  и скалярный потенциал
и скалярный потенциал  , где
, где  - координаты,
- координаты,  - время. Величины
- время. Величины 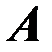 и
и  :
: , (3.49)
, (3.49) . (3.50)
. (3.50) , (3.51)
, (3.51) , (3.52)
, (3.52) - произвольная функция координат и времени, то векторы
- произвольная функция координат и времени, то векторы  , (3.53)
, (3.53) и
и 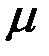 - диэлектрическая и магнитная проницаемости среды. При использовании условия Лоренца (3.53) уравнения для потенциалов в однородной среде (
- диэлектрическая и магнитная проницаемости среды. При использовании условия Лоренца (3.53) уравнения для потенциалов в однородной среде (  и
и  ), получаемые из уравнений Максвелла, приобретают одинаковую форму:
), получаемые из уравнений Максвелла, приобретают одинаковую форму: , (3.54)
, (3.54) , (3.55)
, (3.55) - оператор Лапласа;
- оператор Лапласа;  и
и  - плотности заряда и тока;
- плотности заряда и тока;  - скорость распространения электромагнитного поля в среде.
- скорость распространения электромагнитного поля в среде.