
|
|
ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ ПРОВОДНИКОВЭлектрическим током называется упорядоченное (направленное) движение заряженных частиц. Сила тока – физическая величина, показывающая заряд, проходящий через поперечное сечение проводника за единицу времени:
Один из основных законов цепей постоянного тока - закон Ома для однородного участка цепи: величина тока прямо пропорциональна разности потенциалов (напряжению) на концах проводника и обратно пропорциональна сопротивлению проводника:
где R - сопротивление, которое, как показал Ом, прямо пропорционально длине проводника l и обратно пропорционально площади его поперечного сечения S:
где коэффициент 1 Ом = 1 В/1 А. Электрическое сопротивление проводников зависит от его температуры. У металлов оно возрастает при нагревании проводника, у электролитов уменьшается. В довольно широком интервале температур сопротивление металлических проводников является линейной функцией температуры T:
где R0 - сопротивление при 273 К (0°С), R - сопротивление при температуре T=T0+DT, a - температурный коэффициент сопротивления. Возможны три способа соединения проводников: 1) последовательное, 2) параллельное, 3) комбинированное. При последовательном соединении n проводников сопротивлением Ri каждый общее напряжение, сила тока и сопротивление на участке цепи определяется в виде:
при параллельном:
где Ui, Ii, Ri – напряжение, сила тока и сопротивление для соответствующего проводника.
Если потенциалы точек С и D одинаковы, ток через гальванометр равен нулю. Это происходит при соответствующем выборе сопротивлений R1, R2 , R3, когда:
Из соотношения (1), отображающего баланс моста, следует возможность измерения неизвестного сопротивления Rx:
Обычно в качестве сопротивления R3 используют магазин образцовых сопротивлений. Для балансировки моста подбирают в магазине сопротивлений такое сопротивление R=R3, при котором ток в гальванометре будет равен нулю. При этом достигается наибольшая точность. Выражение (2) упрощается, и искомое сопротивление становится численно равно сопротивлению R, набранному в магазине сопротивлений:
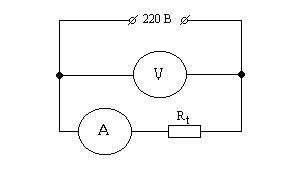
ИЗМЕРЕНИЯ Часть 1. Собрать измерительную цепь (рис. 1). Подключить к зажимам «а» и «б» неизвестное сопротивление Rx1, подбирая сопротивление (в магазине сопротивлений) добиться нулевого показания гальванометра. Записать полученный результат в таблицу. Часть 2. Определить сопротивление электрической лампочки, включенной в осветительную сеть ("горячей" лампочки). Для этого собрать и проверить электрическую цепь (рис. 2). (Внимание! Без разрешения преподавателя или лаборанта электрическую цепь в сеть не включать). Записать показания вольтметра U и амперметра I в таблицу и, по закону Ома для участка цепи, рассчитать сопротивление лампочки в горячем состоянии R по формуле:
где напряжение U берется в вольтах, ток I - в амперах, сопротивление R - в омах. ЗАДАНИЕ 1.Измерить сопротивления двух резисторов (Rx1 и Rx2) порознь с помощью моста постоянного тока. Результаты занести в таблицу. 2.Измерить сопротивление тех же резисторов соединенных первый последовательно, а второй раз параллельно и сравнить значения найденные из опыта, с рассчитанными по формулам:
3. Определить относительную погрешность измерения:
6. Рассчитать температуру T нити накала лампочки согласно формуле:
где Для вольфрама
ЛАБОРАТОРНАЯ РАБОТА № 3э ОПРЕДЕЛЕНИЕ ЭЛЕКТРИЧЕСКОЙ ЕМКОСТИ КОНДЕНСАТОРА БАЛЛИСТИЧЕСКИМ МЕТОДОМ КРАТКАЯ ТЕОРИЯ. Электрической емкостью называется физическая величина, показывающая заряд, который способно накапливать тело при приложении к нему потенциала в 1В:
Конденсатор – тело, способное накапливать достаточно большой заряд. Простейший конденсатор представляет собой два проводника (обкладки), разделенные слоем диэлектрика. Под электроемкостью конденсатора понимают физическую величину, показывающую заряд, который способен накапливать конденсатор при приложении к нему напряжения в 1 В.
Виды конденсаторов: 1. По электроемкости: А) конденсаторы постоянной емкости; Б) конденсаторы переменной емкости. 2. По виду диэлектрика: А) воздушные; Б) электролитические; В) бумажные и т.д. 3. По форме обкладок: А) плоские; Б) сферические и т. д. Конденсаторы соединяются в батареи. Виды соединения конденсаторов: А) последовательное; Б) параллельное.
где n – число конденсаторов. Для двух конденсаторов получим:
Общая электроемкость при параллельном соединении конденсаторов:
Как следует из (1), нахождение значения электроемкости связано с определением заряда Q на обкладках и напряжения U. Напряжение U легко определяется вольтметром V. Заряд Q можно измерить при помощи баллистического гальванометра. Главной частью гальванометра (рис. 2) является подвешенная на вертикальной нити Т рамка F, помещенная в поле постоянного магнита М. Скрепленное с рамкой зеркальце L служит для измерения угла поворота рамки гальванометра в магнитном поле при прохождении по ней электрического тока. Заряд Q, протекающий через рамку, пропорционален первому отбросу светового луча:
где А - постоянная гальванометра, N - число делений шкалы для первого отброса светового луча. Значение постоянной А можно определить, разряжая через гальванометр конденсатор известной ёмкости С, заряженный до напряжения U, тогда заряд конденсатоpa равен:
ИЗМЕРЕНИЯ. I. Собрать схему (рис. 1), подключить конденсатор известной емкости и зарядить его до напряжения, при котором во время разряда конденсатора "зайчик" по шкале гальванометра отклонится на 0,7….0,8 длины шкалы. Далее, определив средний отброс "зайчика" из 5 опытов по разрядке известного конденсатора, найти постоянную гальванометра А, используя (4). 2. Определить емкости двух конденсаторов С1 и C2 по известной постоянной гальванометра А. Для этого подключают вместо образцового сначала конденсатор С1, потом C2. Изменяя напряжение на конденсаторе, добиться отклонения "зайчика" на 0,7...0,8 длины шкалы. Определив средний отброс "зайчика" из 5 опытов, находят значения емкостей C1 и C2 из формулы (4). 3. Определить емкость батареи из двух конденсаторов при параллельном и последовательном соединении. Сравнить результаты опыта с результатами вычисления емкости батареи по формулам (2) и (3).
РЕЗУЛЬТАТЫ
Оценить погрешность результата, сравнивая с рассчитанными по формулам (2) и (3).
ЛАБОРАТОРНАЯ РАБОТА № 4э 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.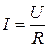 ,
,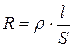 ,
, , зависящий от материала проводника, называют удельным сопротивлением. В Международной системе единиц сопротивление измеряется в омах. 1 Ом - это сопротивление проводника, ток в котором равен 1 ампер, если на концах его поддерживается разность потенциалов 1 вольт:
, зависящий от материала проводника, называют удельным сопротивлением. В Международной системе единиц сопротивление измеряется в омах. 1 Ом - это сопротивление проводника, ток в котором равен 1 ампер, если на концах его поддерживается разность потенциалов 1 вольт: ,
,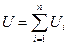 ,
,  , I1=I2 = …..= Ii= In
, I1=I2 = …..= Ii= In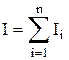 ,
, 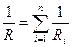 , U1 = U2 = ……= Ui = Un
, U1 = U2 = ……= Ui = Un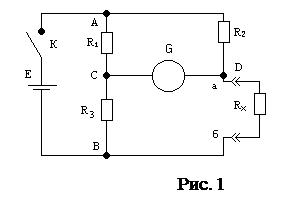 Мостовая схема для измерения сопротивлений приведена на рис. 1. Измерительный мост образован четырьмя резисторами: сопротивления трех из них R1, R2, R3 известны, сопротивление четвертого Rx подлежит измерению. Точками А и В мост присоединен к источнику электрического тока Е, а в диагональ CD моста включен чувствительный гальванометр G (нуль - индикатор).
Мостовая схема для измерения сопротивлений приведена на рис. 1. Измерительный мост образован четырьмя резисторами: сопротивления трех из них R1, R2, R3 известны, сопротивление четвертого Rx подлежит измерению. Точками А и В мост присоединен к источнику электрического тока Е, а в диагональ CD моста включен чувствительный гальванометр G (нуль - индикатор). . (1)
. (1)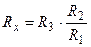 . (2)
. (2) . (3)
. (3) ,
, - последовательное соединение,
- последовательное соединение,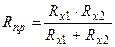 - параллельное соединение.
- параллельное соединение. .
. 4. Измерить с помощью моста постоянного тока сопротивление электрической лампочки (R0) в холодном состоянии.
4. Измерить с помощью моста постоянного тока сопротивление электрической лампочки (R0) в холодном состоянии. .
. ,
, - температурный коэффициент сопротивления.
- температурный коэффициент сопротивления.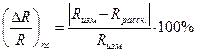

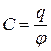 .
. . (1)
. (1)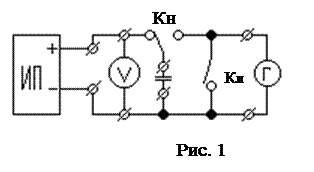 Общая емкость при последовательном соединении конденсаторов:
Общая емкость при последовательном соединении конденсаторов: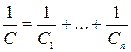 ,
,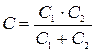 . (2)
. (2) . (3)
. (3)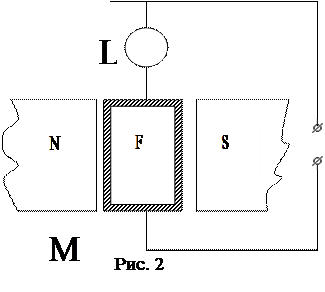 ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Для определения емкости конденсатора пользуются схемой, приведенной на рис.1, где ИП - источник постоянного напряжения, V - вольтметр, Сх- исследуемый конденсатор, Кн - переключатель, позволяющий подключать конденсатор к источнику питания или к гальванометру Г. Параллельно гальванометру подключен ключ Кл, который замыкают на короткое время перед измерением для установки светового луча ("зайчика") в начальное положение.
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Для определения емкости конденсатора пользуются схемой, приведенной на рис.1, где ИП - источник постоянного напряжения, V - вольтметр, Сх- исследуемый конденсатор, Кн - переключатель, позволяющий подключать конденсатор к источнику питания или к гальванометру Г. Параллельно гальванометру подключен ключ Кл, который замыкают на короткое время перед измерением для установки светового луча ("зайчика") в начальное положение. ,
, и
и 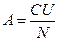 . (4)
. (4)