Асимметричные криптосистемы

Схема шифрования Эль Гамаля

Алгоритм шифрования Эль Гамаля основан на применении больших чисел для генерации открытого и закрытого ключа, криптостойкость же обусловлена сложностью вычисления дискретных логарифмов.

Последовательность действий пользователя:

1. Получатель сообщения выбирает два больших числа P и G, причем P > G.

2. Получатель выбирает секретный ключ - случайное целое число X < P.

3. Вычисляется открытый ключ Y= G ^x mod P.

4. Получатель выбирает целое число K, 1< K< P-1.

5. Шифрование сообщения (M): a= G^K mod P, b=Y ^K M mod P, где пара чисел (a,b) является шифротекстом.

Криптосистема шифрования данных RSA

Предложена в 1978 году авторами Rivest, Shamir и Aldeman и основана на трудности разложения больших целых чисел на простые сомножители.

Алгоритм создания открытого и секретного ключей:

1. Получатель выбирает 2 больших простых целых числа p и q, на основе которых вычисляет n=p*q и функцию Эйлера φ(n)=(p-1)(q-1).

2. Получатель выбирает целое число е (1<e< φ(n)), взаимно простое со значением функции φ(n).

Пара чисел (e,n) публикуется в качестве открытого ключа.

3. Получатель вычисляет целое число d, которое отвечает условию: e*d=1(mod φ(n) ).

Пара чисел (d,n) является секретным ключом.

Шифрование сообщения с использованием открытого ключа:

Если m – сообщение (сообщениями являются целые числа в интервале от 0 до n-1), то зашифровать это сообщение можно как c=m^е mod(n).

Дешифрование сообщения с использованием секретного ключа:

Получатель расшифровывает, полученное сообщение с: m=c^d mod (n).

Задание

Практическая работа состоит из двух частей:

Часть 1 – применение одного из алгоритмов симметричного шифрования;

Часть 2 – шифрование с использованием алгоритма RSA.

Порядок выполнения работы:

Часть 1:

1. Используя один из алгоритмов симметричного шифрования (см. вариант), зашифровать свои данные: фамилию, имя, отчество.

2. Выполнить проверку, расшифровав полученное сообщение.

Часть 2:

1. Написать программу, реализующую алгоритм шифрования и дешифрования сообщения RSA. Входные данные: открытый и секретный ключи (значения n, e, d) и сообщение (m).

2. Используя заданные значения p, q, e, d (см. вариант) зашифровать и дешифровать сообщения m₁, m₂, m₃ (см. вариант).

Содержание отчета

1. Титульный лист

2. Содержание

3. Задание

4. Применение алгоритма симметричного шифрования

5. Применение алгоритма асимметричного шифрования

4.1. Программа шифрования и дешифрования сообщения при помощи алгоритма RSA

4.2. Результаты шифрования и дешифрования заданных сообщений

5. Выводы

Варианты

Вариант – номер по списку в журнале.

Практическая работа №6

«Механизмы контроля целостности данных»

Цель работы

Изучить порядок вычисления и проверки ЭЦП (электронной цифровой подписи)

Теоретические сведения

В настоящее время повсеместное внедрение информационных технологий отразилось и на технологии документооборота внутри организаций и между ними, между отдельными пользователями. Все большее значение в данной сфере приобретает электронный документооборот, позволяющий отказаться от бумажных носителей (или снизить их долю в общем потоке) и осуществлять обмен документами между субъектами в электронном виде. Однако переход от бумажного документооборота к электронному ставит ряд проблем, связанных с обеспечением целостности (подлинности) передаваемого документа и аутентификации подлинности его автора.

Следует отметить, что известные в теории информации методы защиты сообщений, передаваемых по каналам связи, от случайных помех не работают в том случае, когда злоумышленник преднамеренно реализует угрозу нарушения целостности информации. Например, контрольные суммы, используемые для этой цели передатчиком и приемником, могут быть пересчитаны злоумышленником так, что приемником изменение сообщения не будет обнаружено. Для обеспечения целостности электронных документов и установления подлинности авторства необходимо использовать иные методы, отличные от контрольных сумм. Для решения данных задач используют технологию электронно-цифровой подписи.

Электронно-цифровая подпись (ЭЦП) сообщения является уникальной последовательностью, связываемой с сообщением, подлежащей проверке на принимающей стороне с целью обеспечения целостности передаваемого сообщения и подтверждения его авторства.

Процедура установки ЭЦП использует секретный ключ отправителя сообщения, а процедура проверки ЭЦП – открытый ключ отправителя сообщения (рис. 1). Здесь

M – электронный документ, E – электронно-цифровая подпись.

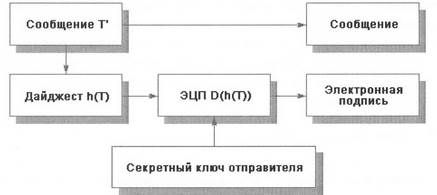
В технологии ЭЦП ведущее значение имеют однонаправленные функции хэширования. Использование функций хэширования позволяет формировать криптографически стойкие контрольные суммы передаваемых сообщений.

Функцией хэширования H называют функцию, сжимающую сообщение произвольной длины M, в значение фиксированной длины H(M) (несколько десятков или сотен бит), и обладающую свойствами необратимости, рассеивания и чувствительности к изменениям. Значение H(M) обычно называют дайджестом сообщения M.

Схема установки ЭЦП (рис. 2):

1. Для документа М формируется дайджест H с помощью заданного алгоритма хэширования.

2. Сформированный дайджест H шифруют на секретном ключе отправителя сообщения. Полученная в результате шифрования последовательность и есть ЭЦП.

Рис. 2 – Схема установки ЭЦП.

Схема проверки ЭЦП (рис. 3):

1. Получатель для проверки ЭЦП должен иметь доступ к самому сообщению М и его ЭЦП.

2. Зная алгоритм хэширования, который был использован при установке ЭЦП, получатель получает дайджест H1 присланного сообщения М.

3. Зная открытый ключ отправителя, получатель дешифрует ЭЦП, в результате чего получает дайджест H2, сформированный на этапе установки ЭЦП.

Рис. 3 – Схема проверки ЭЦП.

Задание

Сформировать ЭЦП к сообщению M' (см. вариант) и произвести проверку целостности принятого сообщения.

Порядок выполнения работы:

1. Разделить лист на две части: слева – сторона отправителя сообщения, справа – получателя.

2. На стороне отправителя выполнить следующие действия:

2.1. Записать сообщение M (см. вариант).

2.2. Сформировать профиль сообщения M’ с помощью упрощенной функции хэширования h(M’) – перемножения всех цифр кроме нуля этого сообщения.

2.3. Создать ЭЦП шифрованием профиля сообщения h(M’) закрытым ключом отправителя Da (значение ключа (d, n) см. в таблице с вариантами задания), т.е. Da (h(M’)) (см. вариант).

3. На стороне получателя выполнить следующие действия:

3.1. Записать сообщение М (его получает получатель вместе с ЭЦП) и ЭЦП Da (h(M’)).

3.2. Сформировать профиль принятого сообщения, M’ с помощью той же функции хэширования h(M’) – перемножения всех цифр кроме нуля этого сообщения (Получателю известен алгоритм хэширования, применяемый на стороне отправителя).

3.3. Создать профиль дешифрованием ЭЦП открытым ключем отправителя (Ea (Da (h(M’)) = h(M’)) (значение ключа (е, n) см. в таблице с вариантами задания).

3.4 Сравнить два профиля сообщения h(M’) (п.3.2 и 3.3). Убедиться в их совпадении.

Содержание отчета

1. Титульный лист

2. Содержание

3. Задание

4. Лист расчета и проверки ЭЦП

5. Выводы

Варианты

Вариант – номер по списку в журнале.

Практическая работа № 7

«Алгоритмы поведения вирусных и других вредоносных программ»

Цель работы

Знакомство с некоторыми алгоритмами поведения вирусных и других вредоносных программ.

Не нашли, что искали? Воспользуйтесь поиском по сайту: