|
|
В любой изолированной системе общий запас энергии сохраняется постоянным.12 Наибольшее количество работы совершается газом в том случае, когда во всё время процесса внешнее давление лишь на ничтожно малую величину меньше собственного давления газа, т.е. когда процесс происходит обратимо. Это наибольшее количество работы мы будем обозначать в дальнейшем через АМ и называть максимальной работой. Рассмотрим обратимое расширение газа, происходящее в цилиндре постоянного сечения s. Обозначим через р внешнее давление, которое приходится преодолевать нашей системе, и через dh бесконечно малое смещение подвижной стенки (поршня). Будем считать, что поршень движется без трения. Зная, что сила, под действием которой смещается поршень, равна ps, можно выразить выполненную работу как произведение этой силы на путь:
или, так как sdh равно изменению объёма dV:
и для конечного изменения объёма от V1 до V2:
При расширении газа, т.е. когда V2 > V1, работа производится против внешнего давления. Уравнения (6)и (7) определяют наибольшее количество работы, которое может произвести газ при расширении от V1 до V2. В обратном процессе – сжатия газа – работу приходится затрачивать извне. Наименьшее количество работы, необходимой для сжатия, равно количеству её, определяемому теми же уравнениями (6)и (7), но, разумеется, противоположное по знаку, так как V2 > V1. Для решения уравнения (7) необходимо знать зависимость давления от объёма. Ограничимся применением этого уравнения только для идеального газа и рассмотрим четыре важнейших вида соответствующих процессов: изобарный, изотермический, адиабатический и изохорный. Изобарный процессотвечает условию постоянства давления. В этом случае интегрирование уравнения (7) приводит к выражению:
т.е. работа изобарного расширения газа равна произведению давления на увеличение объема. На графике (рис. 1), выражающем зависимость давления от объёма (V - р диаграмма), эта работа представляется площадью прямоугольника V1EFV2. Рассматривая расширение одного моля газа, пользуясь уравнением pV = RT и заменяя pV1 на RT1, а pV2 на RT2, можно написать:
Изотермический процесс отвечает условию постоянства температуры. Рассматривая расширение одного моля газа и подставляя
которое легко интегрируется; в результате интегрирования имеем:
Графически (рис. 1) изотермический процесс представляется кривой
Зная, что при постоянной температуре давление обратно пропорционально объёму
Адиабатное расширение газа происходит при одновременном изменении и температуры и давления. Оно отвечает [1, стр. 186] получает теплоты извне, то работа расширения производится им за счет внутренней энергии, а газ охлаждается. Внутренняя энергия идеального газа зависит только от температуры. Следовательно, ΔU равно произведению теплоёмкости газа СV на изменение температуры. Отсюда понижение температуры при адиабатном расширении газа связывается с работой, произведенной газом, соотношением:
где СV - теплоёмкость газа. Графически (рис. 1) адиабатный процесс представляется кривой GH, а рассматриваемая работа – площадью V1FF´´V2. Изохорный процесс отвечает условию постоянства объёма. Уравнение (7) приводит в этом случае к естественному ответу А = 0. Первый закон термодинамики Первый закон термодинамики непосредственно связан с законом сохранения энергии, который устанавливает эквивалентность различных форм её. Первый закон устанавливает связь между количеством теплоты, полученной или выделенной в процессе, количеством произведенной работы и изменением внутренней энергии системы. Ряд следствий, вытекающих из него, имеет большое значение для физической химии и для решения различных производственных задач. Расчёты энергетического и, в частности, теплового баланса, расчёты тепловых эффектов различных процессов могут быть осуществлены с помощью этого закона. Первый закон термодинамики является постулатом; он не может быть по существу доказан логическим путём, а вытекает из суммы всего человеческого опыта. Справедливость этого закона доказывается тем, что ни одно из следствий, к которым он приводит, не находится в противоречии с опытом. В установлении современной формы выражения первого закона термодинамики большую роль сыграли работы Г.И.Гесса[3] (1840), Р.Майера[4] (1842), Джоуля[5] (1847), Гельмгольца[6] (1847) и др. Можно дать несколько формулировок первого закона, которые по существу равноценны одна другой. Закон сохранения энергии в применении его к термодинамическим процессам является одним из таких выражений первого закона термодинамики. Как известно, закон сохранения энергии устанавливает, что если в каком-нибудь процессе энергия одного вида исчезает, то вместо неё появляется энергия в другой форме в количестве, строго эквивалентном первому. Любые переходы энергии соответствуют закону эквивалентности, т.е. разные формы энергии переходят друг в друга в строго эквивалентных, всегда одинаковых соотношениях. Отсюда вытекает, что в любой изолированной системе общий запас энергии сохраняется постоянным. Так как все виды энергии являются соответствующими формами движения материи, то закон сохранения энергии выражает неуничтожаемость движения. Энгельс подчёркивает, что эту неуничтожаемость движения следует понимать не только в количественном, но и в качественном смысле, т.е. как сохранение безграничной способности движения материи к качественным превращениям из одной формы в другую. Поскольку работа представляет собой одну из форм перехода энергии, то из указанных положений следует невозможность создания вечного двигателя (perpetuum mobile) первого рода, т.е. такого механизма (машины), который бы давал возможность получить работу, не затрачивая на это соответствующего количества энергии. Иначе говоря вечный двигатель первого рода невозможен. Большое значение имеет следующая формулировка первого закона, непосредственно вытекающая из постоянства запаса внутренней энергии изолированной системы: В любом процессе приращение внутренней энергии ΔU = U2 - U1какой-либо системы равно количеству q сообщённой системе теплоты минус количество А работы, совершённой системой. ΔU = q - A (14) (все величины, разумеется, должны быть выражены в одинаковых единицах измерения). Это соотношение следует рассматривать как математическое выражение первого начала термодинамики. Пользуясь им, можно дать термодинамическое определение понятия внутренней энергии как величины, приращение которой в процессе равно сообщённой системе теплоте, сложенной с работой, совершённой над системой внешними по отношению к ней силами. Из трёх величин, входящих в соотношение (14), только одна – изменение внутренней энергии ΔU – однозначно определяется начальным и конечным состояниями системы и не зависит от пути перехода. Остальные же две таким свойством не обладают. Каждая их них в отдельности зависит от способа совершения процесса, хотя разность их от этого не зависит. В качестве примера рассмотрим процесс зарядки и разрядки аккумуляторной батареи. Из закона сохранения энергии следует, что если мы при зарядке батареи до определённого состояния затрачиваем некоторое количество энергии, то при обратной разрядке до исходного состояния она отдаст то же количество энергии.[7] Очевидно, что в зависимости от того, как будет производиться эта разрядка, выделение энергии может происходить в различных формах. Можно, например, всю энергию израсходовать на работу электромотора, который будет совершать механическую работу (подъём груза, сжатие газа с помощью компрессора и др.). В этом случае q = 0 и ΔU = - A. Можно разрядить батарею, соединяя её с электронагревательными приборами, расходую всю выделяющуюся энергию для получения теплоты. В этом случае А = 0 и ΔU = q. Можно какую-нибудь часть энергии израсходовать на получение работы, а другую часть – на получение теплоты. Однако сумма полученной теплоты и произведенной работы будет одинаковой, если в разных случаях как начальные, так и конечные состояния аккумуляторов были одинаковы. Эта сумма равна убыли внутренней энергии системы и не зависит от пути её перехода; она не зависит, в частности, от того, в обратимой или необратимой форме осуществлялись те или другие стадии процесса.[8] Для процессов, связанных лишь с бесконечно малыми изменениями, уравнению (14)удобно придать вид: где dU - полный дифференциал энергии системы;δq иδA - бесконечно малые количества теплоты и работы. Из уравнения (15) вытекает ряд следствий. Так, в частности, для кругового процесса (так как в нём ΔU = U2 - U1 = 0) всегда должно соблюдаться равенство q = A. Во многих процессах работа совершается только против внешнего давления. В этих случаях для изотермического процесса δA = pdV и уравнение (15) принимает вид: dU = δq - pdV (16) Отсюда для изохорных процессов (dV = 0): δq = dU (17) Из определения энтальпии (2) имеем: dH = dU + pdV + Vdp (18) откуда для изобарных процессов (dp = 0) = следует: dH = dU + pdV (19) Согласно уравнению (2) ΔH = ΔU + Δ(pV) (20) где Δ(pV) = p2V2 - p1V1 (21)
ΔH = ΔU + pΔV (22) Для идеальных газов pV при постоянной температуре для данного количества газов постоянно. Произведение pV зависит от числа молей газа и для n молей газа pV = nRT. Следовательно, если в реакции расходуется n1 молей газообразных веществ и происходит образование n2 молей газообразных продуктов, то Δ(pV) = (n2 - n1)RT = ΔnRT и ΔH = ΔU + ΔnRT (23) Если реакция происходит в конденсированных фазах, т.е. ни одно из исходных веществ или продуктов реакции не находится в газообразном состоянии, то различие между ΔH и ΔU незначительно и им большей частью можно пренебречь. Пример.Определить ΔU реакции СаСО3 = СаО + СО2 при 900°С, если ΔН её при этой температуре равно 42,560 ккал/моль. Решение. В этой реакции Δn = 1. Следовательно: ΔU = ΔH - RT т.е. ΔU = 42560 - 1,987(900 + 273) = 40229 кал/моль = 40,229 ккал/моль
Теперь можно вывести два важных соотношения для определения теплоёмкостей. В общем случае истинная теплоёмкость определяется как отношение бесконечно малого количества теплоты, сообщаемой телу, к тому изменению температуры, которое этим вызывается, т.е.
и для изобарных процессов
Оба эти равенства справедливы для любых веществ и для любого агрегатного состояния. Закон Гесса Г.И. Гесс (1840) описал закон, получивший его имя и являющийся основным законом термохимии. Закон Гесса устанавливает, что если из данных исходных веществ можно различными путями получить заданные конечные продукты, то независимо от путей получения, т.е. от вида промежуточных реакций, суммарный тепловой эффект для всех путей будет одним и тем же. Иначе говоря, тепловой эффект химических реакций зависит только от вида и состояния исходных веществ и конечных продуктов, но не зависит от пути перехода. Закон Гесса является вполне строгим только для процессов, протекающих при постоянном объёме (когда тепловой эффект равен ΔU) или при постоянном давлении (когда тепловой эффект равен ΔН). Для этих процессов он легко выводится из общего уравнения первого начала (закон Гесса был установлен раньше, чем было введено уравнение первого начала).
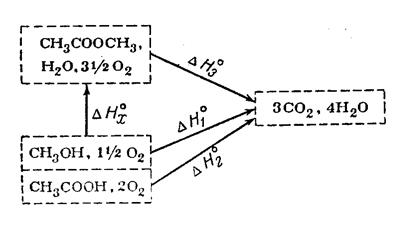
1) непосредственно реакцией, тепловой эффект которой равен ΔН1; 2) реакциями, тепловые эффекты которых равны соответственно ΔН2 , ΔН3, и ΔН4; 3) рядом реакций, тепловые эффекты которых равны ΔН5 , ΔН6 ,ΔН7 и ΔН8 . Закон Гесса утверждает, что эти тепловые
ΔН1 = ΔН2 + ΔН3 + ΔН4 = ΔН5 + ΔН6 + ΔН7 + ΔН8 (26)
СО2 [1, стр. 191] Все эти три процесса находят широкое ΔН1 = ΔН2 + ΔН3 пользуясь которым легко определить один из них, если другие два известны. В нашем случае можно сравнительно легко измерить тепловые эффекты первого и третьего процессов, но сжигание угля до окиси углерода при невысоких температурах затруднительно. Поэтому возможность определить его тепловой эффект расчётным путём является весьма ценной. Из предыдущего получаем: ΔН2 = ΔН1 - ΔН3 (28) Численные значения ΔН1 и ΔН2 зависят от вида применяемого угля. Величина ΔН2 с этим, очевидно, не связана. Количество теплоты, выделяющейся при сгорании одного моля СО при постоянном давлении, составляет 67,636 ккал (при 25°С). Пусть, например, нас интересует величина ΔН2 при 25°С для угля, для которого при этой температуре ΔН1 равно -94,0 ккал/моль. Согласно уравнению (28), определяем: ΔН2 = -94,0 + 67,6 = -26,4 ккал/моль Закон Гесса широко применяется при различных термохимических расчётах; он даёт возможность вычислить тепловые эффекты процессов, для которых экспериментальные данные отсутствуют, а во многих случаях – и для таких, для которых они не могут быть измерены в нужных условиях, или когда процессы ещё не осуществлялись. Это относится как к химическим реакциям, так и к процессам растворения, испарения, кристаллизации, адсорбции и др. Однако, применяя данный закон, следует строго соблюдать условия, лежащие в его основе. Прежде всего необходимо, чтобы в обоих процессах были действительно одинаковы начальные состояния и действительно одинаковы конечные состояния. При этом одинаковыми должны быть не только химические составы продуктов, но и условия их существования (температура, давление и пр.) и агрегатное состояние, а для кристаллических веществ – также и кристаллическая модификация. Так, образование одного моля газообразной и одного моля жидкой Н2О из Н2 и О2 при 25°С сопровождается выделением соответственно 57,798 и 68,317 ккал; разность составляет 10,519 ккал и равна теплоте испарения моля воды в этих условиях. При точных расчётах в случае, если какое-либо из веществ, участвующих в реакциях, находится в высокодисперсном (т.е. сильно раздробленном) состоянии, существенной оказывается иногда даже и одинаковость степени дисперсности веществ и пр. Очевидно, тепловой эффект будет различен также в зависимости от того, будут ли получаемые или исходные вещества находиться в чистом состоянии или в растворе, отличаясь на величину теплоты растворения. Опытное определение тепловых эффектов Для определения тепловых эффектов, сопровождающих химические реакции, применяются специальные приборы, называемые калориметрами. Калориметрическое определение ведётся так, чтобы вся химическая энергия выделялась в виде теплоты или частично затрачивалась на совершение внешней работы расширения газа, которая может быть учтена. Простейший калориметр может быть собран по схеме, показанной на рис. 4. Химическая реакция ведётся в сосуде Дьюара 1. Он представляет собой стеклянный сосуд с посеребренными изнутри двойными стенками, из пространства между которыми выкачан воздух, вследствие чего стенки сосуда почти не проводят теплоты. Для более равномерного теплообмена с окружающей средой сосуд всё же помещают в обычно в большой термостат[9] 2, заполненный водой. Во время опыта температура термостата поддерживается Зная теплоёмкость системы (которая определяется предварительно), можно вычислить При экспериментальном определении тепловых эффектов химических реакций возникают ошибки и неточности, обусловленные главным образом теплообменом прибора с окружающей средой. Чтобы уменьшить теплообмен, ведут реакцию возможно быстрее и температуру калориметра в начале опыта поддерживают по возможности равной температуре воздуха в лаборатории. При определении изменения температуры тоже может появиться ряд неточностей. Большей частью для измерения температуры пользуются специальными калориметрическими термометрами. Кроме того, так как не весь столбик ртути находится при той температуре, какая имеется в калориметре, необходимо делать поправку на «выступающий столбик». На основе калориметрических определений накоплено много данных о тепловых эффектах различных химических реакций, процессов растворения, плавления, испарения и пр. Расчёты тепловых эффектов химических реакций При расчётах тепловых эффектов различных химических реакций на основе закона Гесса особое значение имеют два вида тепловых эффектов - теплота образования и теплота сгорания. Теплотой образования называется тепловой эффект реакции образования данного соединения из простых веществ, отвечающих наиболее устойчивому состоянию рассматриваемого элемента при данной температуре.[10] Например, теплота образования 1 моль СаСО3 равна тепловому эффекту реакции образования карбоната кальция в данной его кристаллической модификации из металлического кальция, углерода (в виде графита) и газообразного кислорода: Са(м) + С(гр) + Хотя такие реакции большей частью неосуществимы на практике, однако их тепловые эффекты находят широкое применение в качестве вспомогательных расчётных величин. Теплоту образования соединения из простых веществ следует отличать от атомарной теплоты образования. Образование молекулы из свободных атомов всегда сопровождается выделением энергии. При образовании же какого-нибудь соединения из простых веществ теплота может и поглощаться, так как образование свободных атомов из простых веществ обычно требует затраты энергии. Так, образование ацетилена из атомов углерода и водорода сопровождается выделением энергии в количестве 393,4 ккал/моль, а образование ацетилена из графита и молекул Н2 сопровождается поглощением 54,2 ккал/моль, так как разложение молекул Н2 на атомы требует затраты энергии в количестве 104,2 ккал/моль и для получения свободных атомов углерода из графита необходимо затратить 171,7 ккал/моль. Таким образом, на образование свободных атомов углерода и водорода в количестве, необходимом для образования одного моля ацетилена, требуется 104,2 + 2∙171,7 = 447,6 ккал. Теплоту образования можно относить к любому количеству вещества, но чаще всего (также как и в рамках настоящего курса) её относят к одному молю соединения. Тепловые эффекты реакции зависят от условий проведения реакций (температуры, давления и пр.). В настоящее время различные справочные значения тепловых эффектов и других величин относят обычно к стандартному состоянию веществ. В качестве стандартного состояния индивидуальных жидких и твёрдых веществ принимают состояние их при данной температуре и при давлении, равном 1 атм, а для индивидуальных газов – такое их состояние (большей частью гипотетическое), когда при данной температуре и давлении, равном 1 атм, они обладают свойствами идеального газа. Все величины, относящиеся к стандартному состоянию веществ, отмечают верхним индексом ° (ΔН°обр., Н°Т - Н°0 , С°р и т.д.) и называют стандартными (стандартная теплота образования, стандартная энтальпия). В области обычных давлений изменение давления слабо влияет на тепловые эффекты реакций и энтальпию веществ, так как внутренняя энергия идеального газа не зависит от давления, а в конденсированном состоянии сжимаемость веществ мала. Однако многие другие величины, как, например, энтропия газов, сильно зависят от давления. Для облегчения расчётов справочные данные относят в первую очередь к одной температуре 25,00°С (298,15°К), принимаемой в качестве стандартной температуры. (В индексах при тех или других величинах эта температура сокращённо указывается 298). Конечно, справочные данные даются и для дпугих температур. Условие о стандартной температуре вполне не зависит от условия о стандартных состояниях. Пользуясь справочными данными, можно легко рассчитать тепловой эффект любой химической реакции, если известны теплоты образования всех веществ, участвующих в реакции. Из закона Гесса следует, что тепловой эффект реакции равен разности между теплотами образования всех веществ, указанных в правой части уравнения, и теплотами образования всех веществ, указанных в левой части уравнения (взятых, разумеется, с коэффициентами, равными коэффициентам перед формулами этих веществ в уравнении самой реакции). Обратимся к произвольной реакции вида bB + dD = qQ + rR (28) где b, d, q и r - коэффициенты при формулах веществ B, D, Q иRв уравнении реакции (стехиометрические коэффициенты). Если через ΔН°обр.В, ΔН°обр.D, ΔН°обр.Q и ΔН°обр.R обозначить теплоты образования этих веществ, то тепловой эффект реакции ΔН°х = (qΔН°обр.Q + rΔН°обр.R) - (bΔH°обр.B + dΔH°обр.D) (29) или в общем случае, обозначая сумму знаком Σ
Это уравнение даёт возможность рассчитать любую из содержащихся в нём величин, если известны значения остальных. Наиболее часто оно используется для определения теплового эффекта реакции на основе известных значений теплот образования веществ, участвующих в реакции. Рассмотрим для примера реакцию получения при 25°С кристаллического Al2(SO4)3 из кристаллической Al2O3 (α-корунд) и газообразного SO3: Al2O3 + 3SO3 = Al2(SO4)3 (31) Воспользуемся приведенными в таблицах для этих соединений значениями изобарных теплот их образования в стандартных условиях: для Al2O3 ΔHобр.1 = - 400,5 ккал; для SO3 (газ) ΔHобр 2. = - 94,6 ккал и для Al2(SO4)3 ΔHобр.3 = - 822,8 ккал. Отсюда, в соответствии с уравнением (30) определяем для реакции (31): ΔНх = ΔНобр. 3 – (ΔНобр. 1 + 3ΔНобр. 2) или ΔНх = -822,8 – (-400,5 – 3·94,6) = - 138,5 ккал
Таким образом, знание теплот образования всех веществ, участвующих в реакции, действительно даёт возможность рассчитать Теплотой сгорания называется тепловой эффект реакции окисления данного соединения кислородом с образованием высших окислов соответствующих элементов или соединения этих окислов. Для органических соединений, в частности, теплотой сгорания называется тепловой эффект реакции полного сгорания данного соединения до двуокиси углерода, водяных паров (или жидкой воды) и других соответствующих продуктов. Сгорание протекает в виде быстрой реакции, тепловой эффект которой может быть измерен с помощью калориметра. Теплоты сгорания топлива характеризуют его теплотворную способность.Теплоты сгорания определяют путём сжигания навески вещества в особом приборе – калориметрической бомбе, помещённой в калориметр. Чтобы сгорание шло достаточно энергично, в бомбу вводят чистый кислород под высоким давлением (до 25 атм). Если известны теплоты сгорания всех веществ, участвующих в реакции, то по ним можно рассчитать и тепловой эффект самой реакции. Из закона Гесса следует, что тепловой эффект реакции равен разности между теплотами сгорания веществ, указанных в левой части уравнения, и теплотами сгорания веществ, указанных в правой части уравнения реакции (взятых, разумеется, с соответствующими стехиометрическими коэффициентами). Так, для реакции (28), если
или в общем случае
Необходимо, чтобы все теплоты сгорания относились к одинаковым условиям – изобарным или изохорным. К этим же условиям относится и полученное значение теплового эффекта реакции. На рис. 6 показана схема расчёта для реакции образования сложного 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
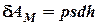 (5)
(5) (6)
(6)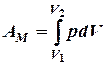 (7)
(7)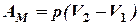 (8)
(8)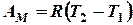 (9)
(9)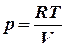 в уравнение (7), получаем выражение:
в уравнение (7), получаем выражение: (10)
(10) (11)
(11)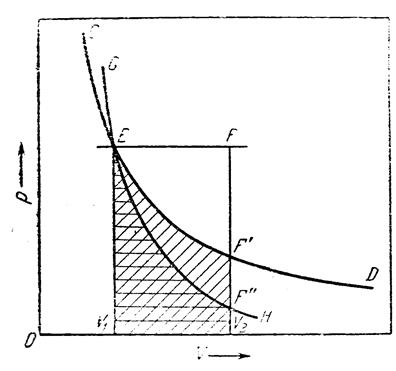 CD, а рассматриваемая работа - площадью V1EF´V2.
CD, а рассматриваемая работа - площадью V1EF´V2. , полученному уравнению можно придать вид:
, полученному уравнению можно придать вид: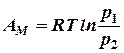 (12)
(12)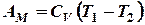 (13)
(13) dU = δq - δA (15)
dU = δq - δA (15)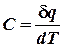 . Отсюда следует, что для изохорных процессов
. Отсюда следует, что для изохорных процессов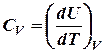 (24)
(24)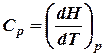 (25)
(25) Представим себе процесс превращения исходных веществ А1, А2, А3 … в продукты В1, В2, В3 …, причём как показано на рис. 2, превращение это может быть осуществлено различными путями:
Представим себе процесс превращения исходных веществ А1, А2, А3 … в продукты В1, В2, В3 …, причём как показано на рис. 2, превращение это может быть осуществлено различными путями: Для большей наглядности в качестве исходных веществ возьмём кислород и уголь (считая его чистым углеродом), а в качестве конечного продукта СО2 (рис. 3). Переход от исходных веществ к конечному можно осуществить, непосредственно сжигая уголь до СО2. Но можно также провести процесс в две стадии, получая в первой из них СО и
Для большей наглядности в качестве исходных веществ возьмём кислород и уголь (считая его чистым углеродом), а в качестве конечного продукта СО2 (рис. 3). Переход от исходных веществ к конечному можно осуществить, непосредственно сжигая уголь до СО2. Но можно также провести процесс в две стадии, получая в первой из них СО и постоянной. Сосуд покрыт медной крышкой 3 с тремя отверстиями: для термометра 4, мешалки 5 и для пробирки 6. В сосуд и пробирку помещают навески реагирующих веществ, где они находятся до тех пор, пока не уравняется температура всех частей прибора. Определив температуру реагирующих веществ до начала реакции, проводят реакцию и определяют температуру в калориметре после реакции.
постоянной. Сосуд покрыт медной крышкой 3 с тремя отверстиями: для термометра 4, мешалки 5 и для пробирки 6. В сосуд и пробирку помещают навески реагирующих веществ, где они находятся до тех пор, пока не уравняется температура всех частей прибора. Определив температуру реагирующих веществ до начала реакции, проводят реакцию и определяют температуру в калориметре после реакции. О2 (г) = СаСО3 (кр)
О2 (г) = СаСО3 (кр) (30)
(30)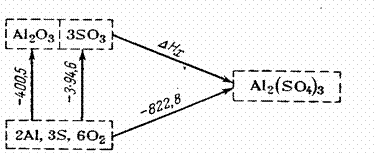 На рис. 5 показана схема произведенного расчёта.
На рис. 5 показана схема произведенного расчёта.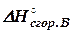 ,
, 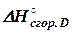 ,
, 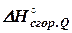 и
и 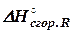 обозначают теплоты сгорания веществ B, D, QиR, тепловой эффект реакции
обозначают теплоты сгорания веществ B, D, QиR, тепловой эффект реакции (32)
(32)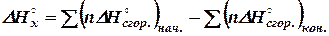 (33)
(33)