
|
|
Кодирование с минимальной избыточностьюДля практики важно, чтобы коды сообщений имели по возможности наименьшую длину. Алфавитное кодирование пригодно для любых сообщений, то есть S = A*. Если больше про множество S ничего не известно, то точно сформулировать задачу оптимизации затруднительно. Однако на практике часто доступна дополнительная информация. Например, для текстов на естественных языках известно распределение вероятности появления букв в сообщении. Использование такой информации позволяет строго поставить и решить задачу построения оптимального алфавитного кодирования. Минимизация длины кода сообщения Если задана разделимая схема алфавитного кодирования Если заданы конкретное сообщение и конкретная схема кодирования, то нетрудно подобрать такую перестановку элементарных кодов, при которой длина кода сообщения будет минимальна. Пусть k1,…,kn – количества вхождений букв a1,...,an в сообщение S,а l1,…,ln – длины элементарных кодов
Отсюда вытекает алгоритм назначения элементарных кодов, при котором длина кода конкретного сообщения S будет минимальна: нужно отсортировать буквы в порядке убывания количества вхождений, элементарные коды отсортировать в порядке возрастания длины и назначить коды буквам в этом порядке. ЗАМЕЧАНИЕ Этот простой метод решает задачу минимизации длины кода только для фиксированного сообщения S и фиксированной схемы
Цена кодирвания Пусть заданы алфавит Для каждой (разделимой) схемы
и называется средней ценой (или длиной) кодирования Пример Для разделимой схемы А={a,b}, B={0,1}, Обозначим Очевидно, что всегда существует разделимая схема Алфавитное (разделимое) кодирование Алгоритм Фано Следующий рекурсивный алгоритм строит разделимую префиксную схему алфавитного кодирования, близкого к оптимальному.
Алгоритм 6.1.Построение кодирования, близкого к оптимальному Вход: P : array [1..n] of real – массив вероятностей появления УКВ в сообщении, упорядоченный по невозрастанию; Выход: C : array [1..n, 1..L] of 0..1 – массив элементархых кодов. Fano (1, n, 0) { вызов рекурсивной процедуры Fano }
Основная работа по построению элементарных кодов выполняется следующей рекурсивной процедурой Fano. Вход: b – индекс начала обрабатываемой части массива P, е – индекс конца обрабатываемой части массива P, к – длина уже построенных кодов в обрабатываемой части массива С. Выход:заполненный массив С. if e > b then k:=k+1 { место для очередного разряда в коде } m:=Med (b, e) { деление массива на две части } for I from b to e do C [i,k] := I > m { в первой части добавляем 0, во второй - 1 } end for Fano (b, m, k) { обработка первой части } Fano (m+1, e, k) { обработка второй части } end if Функция Med находит медиану указанной части массива P [b..e], то есть определяет такой индекс m ( Вход:b – индекс начала обрабатываемой части массива P, e – индекс концап обрабатываемой части массива P. Выход: m – индекс медианы, то есть Sb:= {сумма элементов первой части } for i from b to e-1 do Sb:=Sb+P[i] { вначале все, кроме последнего } end for Se:=P[e] { сумма элементво второй части } M := e { начинаем искать медиану с конца } repeat d:=Sb-Se { разность сумм первой и второй части } m:=m-1 { сдвигаем границу медианы вниз } Sb:=Sb-P[m]; Se:=Se+P[m] until |Sb-Se| return m
Обоснование При каждом удлинении кодов в одной части коды удлиняются нулями, а в другой – единицами. Таким образом, коды одной части не могут быть префиксами другой. Удлинение кода заканчивается тогда и только тогда, когда длина части равна 1, то есть остается единственный код. Таким образом, схема по построению префиксная, а потому разделимая.
Пример Коды, построенные алгоритмом Фано для заданного распределения (n=7).
Оптимальное кодирование Оптимальное кодирование обладает определенными свойствами, которые можно использовать для его построения.
ЛЕММА Пусть Доказательство От противного. Пусть i<j, pi>pj и li>lj. Тогда рассмотрим
Имеем:
что противоречит тому, что Таким образом, не ограничивая общности, можно считать, что
ЛЕММА Если Доказательство От противного 1. Пусть кодовое слово максимальной длины одно и имеет вид 2. Пусть теперь два кодовых слова ТЕОРЕМАЕсли то кодирование со схемой
является оптимальным префиксным кодированием для распределения вероятностей Pn=p1,…,pj-1,pj+1,…,pn-1,q’,q’’.
Доказательство
5. 6. 7. Алгоритм Хаффмана Следующий рекурсивный алгоритм строит схему оптимального префиксного алфавитного кодирования для заданного распределения вероятностей появления букв.
Алгоритм 6.2.Построение оптимальной схемы – рекурсивная процедура Huffman Вход:n – количество букв, P : array [1..n] of real – массив вероятностей букв, упорядоченный по убыванию. Выход: C : array [1..n,1..L] of 0..1 – массив элементарных кодов, l : array [1..n] of 1..L – массив длин элементарных кодов схемы оптимального префиксного кодирования. if n=2 then C [1, 1] := 0; l[1] := 1; { первый элемент } C [2, 1] := 1; l[2] := 1; { Второй элемент } else q := P[n-1]+P[n] { сумма двух последних вероятностей } j := Up (n, q) { поиск места и вставка суммы } Huffman (P, n-1) { рекурсивный вызов } Down (n, j) { достраивание кодов } End if Функция Up находит в массиве P место, в котором должно находиться число q (см. предыдущий алгоритм) и вставляет это число, сдвигая вниз остальные элементы. Вход:n – длина обрабатываемой части массива p, q – вставляемая сумма. Выход:измененный массив P.
for I from n-1 downto 2 do if P [i-1] <= q then P[i] := P[i-1] { сдвиг элемента массива } else j:=i-1 { определение места вставляемого элемента } exit for I { все сделано – цикл не нужно продолжать } end if end for P[j] := q; return j
Процедура Down строит оптимальный код для n букв на основе построенного оптимального кода для n-1 буквы. Для этого код буквы с номером j временно исключается из массива C путем сдвига вверх кодов букв с номерами, большими j, а затем в конец обрабатываемой части массива С добавляется пара кодов, полученных из кода буквы с номером j удлинением на 0 и 1, соответственно. Здесь C[I,*] означает вырезку из массива, то есть i-ю строку массива С. Вход:n – длина обрабатываемой части массива P, j – номер «разделяемой» буквы. Выход:оптимальные коды в первых n элементах массивов С и l.
c := C [j, *] { запоминание кода буквы j } l := l[j] { и длины этого кода } for i from j to n-2 do C[I,*]:=C[i+1,*] { сдвиг кода } l[i] := l[i+1] { и его длины } end for C[n-1,*]:=c; C[n,*] := c { копирование кода буквы j } C[n-1,l+1]:=0; C[n, l+1] := 1 { наращивание кодов } L[n-1] := l+1; l[n] := l+1 { и увеличение длин }
Обоснование Для пары букв при любом распределении вероятностей оптимальное кодирование очевидно: первой букве нужно назначить код 0, а второй – 1. Именно это и делается в первой части оператора if основной процедуры Huffman. Рекурсивная часть алгоритма в точности следует доказательству теоремы предыдущего подраздела. С помощью функции Up в исходном упорядоченном массиве P отбрасываются две последние (наименьшие) вероятности, и их сумма вставляется в массив P, так чтобы массив (на единицу меньшей длины) остался упорядоченным. Заметим, что при этом место вставки сохраняется в локальной переменной j. Так происходит до тех пор, пока не останется массив их двух элементов, для которого оптимальный код известен. После этого в обратном порядке строятся оптимальные коды для трех, четырех и т. д. элементов. Заметим, что при этом массив вероятностей Р уже не нужен – нужна только последовательность номеров кодов, которые должны быть изъяты из массива кодов и продублированы в конце с добавлением разряда. А эта последовательность храниться в экземплярах локальной переменной j, соответствующих рекурсивным вызовам процедуры Huffman. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
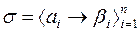 , то любая схема
, то любая схема  , где
, где 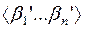 является перестановкой
является перестановкой  , также будет разделимой. Если длины элементарных кодов равны, то перестановка элементарных кодов в схеме не влияет на длину кода сообщения. Но если длины элементарных кодов различны то длина кода сообщения зависит от состава букв в сообщении и от того, какие элементарные коды каким буквам назначены.
, также будет разделимой. Если длины элементарных кодов равны, то перестановка элементарных кодов в схеме не влияет на длину кода сообщения. Но если длины элементарных кодов различны то длина кода сообщения зависит от состава букв в сообщении и от того, какие элементарные коды каким буквам назначены. , соответственно. Тогда, если
, соответственно. Тогда, если  и
и  , то
, то  . Действительно, пусть kj=k+a, ki=k и lj=l, li=l+b, где a,b
. Действительно, пусть kj=k+a, ki=k и lj=l, li=l+b, где a,b  0. Тогда
0. Тогда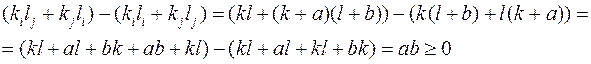
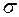 .
. и вероятности появления букв в сообщении
и вероятности появления букв в сообщении  (pi – вероятность появления буквы ai). Не ограничивая общности, можно считать, что pi+…+pn=1 и
(pi – вероятность появления буквы ai). Не ограничивая общности, можно считать, что pi+…+pn=1 и  (то есть можно сразу исключить буквы, которые не могут появиться в сообщении, и упорядочить буквы по убыванию вероятности их появления).
(то есть можно сразу исключить буквы, которые не могут появиться в сообщении, и упорядочить буквы по убыванию вероятности их появления). ) определяется следующим образом:
) определяется следующим образом: , где
, где 
 при распределении вероятностей
при распределении вероятностей  цена кодирования составляет 0.5*1+0.5*2=1.5, а при распределении вероятностей
цена кодирования составляет 0.5*1+0.5*2=1.5, а при распределении вероятностей  она равна 0.9*1+0.1*2=1.1.
она равна 0.9*1+0.1*2=1.1.
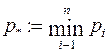

 . Такая схема называется схемой равномерного кодироваия. Следовательно,
. Такая схема называется схемой равномерного кодироваия. Следовательно,  и достаточно учитывать только такие схемы, для которых
и достаточно учитывать только такие схемы, для которых  , где li целое и
, где li целое и  . Таким образом, имеется лишь конечное число схем
. Таким образом, имеется лишь конечное число схем  . Следовательно, существует схема
. Следовательно, существует схема  , на которой инфимум достигается:
, на которой инфимум достигается: 
 , называется кодированием с минимальной избыточностью, или оптимальным кодированием, для распределения вероятностей P.
, называется кодированием с минимальной избыточностью, или оптимальным кодированием, для распределения вероятностей P. .
. ), что сумма элементов P [b..m] наиболее близка к сумме элементов P [m+1..e].
), что сумма элементов P [b..m] наиболее близка к сумме элементов P [m+1..e].
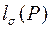
 . Тогда если pi>pj, то
. Тогда если pi>pj, то  .
.
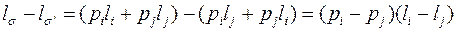
 .
. , где b=0 V b=1. Имеем:
, где b=0 V b=1. Имеем: 
 . Так как схема префиксная, то слова
. Так как схема префиксная, то слова  не являются префиксами
не являются префиксами  . С другой стороны,
. С другой стороны,  , а значит,
, а значит,  было бы префиксом
было бы префиксом  . Тогда схема
. Тогда схема  тоже префиксная, причем
тоже префиксная, причем  , что противоречит оптимальности
, что противоречит оптимальности  и
и  максимальной длины отличаются не в последнем разряде, то есть
максимальной длины отличаются не в последнем разряде, то есть  , причем
, причем 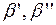 не являются префиксами для
не являются префиксами для  и наоборот. Тогда схема
и наоборот. Тогда схема  также является префиксной, причем
также является префиксной, причем  - схема оптимального префиксного кодирования для распределения вероятностей
- схема оптимального префиксного кодирования для распределения вероятностей  и
и  , причем
, причем 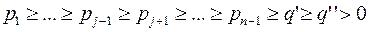 ,
,
 было префиксным, то
было префиксным, то  тоже будет префиксным по построению.
тоже будет префиксным по построению.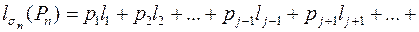



 оптимальна для Pn. Тогда по предшествуюещй лемме
оптимальна для Pn. Тогда по предшествуюещй лемме  . Положим
. Положим  и рассмотрим схему
и рассмотрим схему  , где j определено так, чтобы
, где j определено так, чтобы  .
.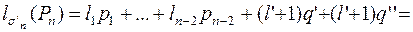


 - префиксное, значит
- префиксное, значит  тоже префиксное.
тоже префиксное. .
. , но
, но