
|
|
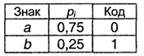
Блочное двоичное кодированиеВернемся к проблеме оптимального кодирования. Пока что наилучший результат (наименьшая избыточность) был получен при кодировании по методу Хаффмана - для русского алфавита избыточность оказалась менее 1 %. При этом указывалось, что код Хаффмана улучшить невозможно. На первый взгляд это противоречит первой теореме Шеннона, утверждающей, что всегда можно предложить способ кодирования, при котором избыточность будет сколь угодно малой величиной. На самом деле это противоречие возникло из-за того, что до сих пор мы ограничивали себя алфавитным кодированием. При алфавитном кодировании передаваемое сообщение представляет собой последовательность кодов отдельных знаков первичного алфавита. Однако возможны варианты кодирования, при которых кодовый знак относится сразу к нескольким буквам первичного алфавита (будем называть такую комбинацию блоком) или даже к целому слову первичного языка. Кодирование блоков понижает избыточность. В этом легко убедиться на простом примере. Пусть имеется словарь некоторого языка, содержащий n=16000 слов (это, безусловно, более чем солидный словарный запас!). Поставим в соответствие каждому слову равномерный двоичный код. Очевидно, длина кода может быть найдена из соотношения K(A, 2)≥log2n≥ 13,97 = 14. Следовательно, каждое слово кодируется комбинацией из 14 нулей и единиц - получатся своего рода двоичные иероглифы. Например, пусть слову "ИНФОРМАТИКА" соответствует код 10101011100110, слову "НАУКА" - 00000000000001, а слову "ИНТЕРЕСНАЯ" -00100000000010; тогда последовательность: очевидно, будет означать "ИНФОРМАТИКА ИНТЕРЕСНАЯ НАУКА". 76 Легко оценить, что при средней длине русского слова K(r) =6,3 буквы (5,3 буквы + пробел между словами) средняя информация на знак первичного алфавита оказывается равной I(A)=K(A,2)=14/6,3 = 2,222 бит, что более чем в 2 раза меньше, чем 5 бит при равномерном алфавитном кодировании. Для английского языка такой метод кодирования дает 2,545 бит на знак. Таким образом, кодирование слов оказывается более выгодным, чем алфавитное. Еще более эффективным окажется кодирование в том случае, если сначала установить относительную частоту появления различных слов в текстах и затем использовать код Хаффмана. Подобные исследования провел в свое время Шеннон: по относительным частотам 8727 наиболее употребительных в английском языке слов он установил, что средняя информация на знак первичного алфавита оказывается равной 2,15 бит. Вместо слов можно кодировать сочетания букв - блоки. В принципе блоки можно считать словами равной длины, не имеющими, однако, смыслового содержания. Удлиняя блоки и применяя код Хаффмана теоретически можно добиться того, что средняя информация на знак кода будет сколь угодно приближаться к L. Пример 3.2. Пусть первичный алфавит состоит из двух знаков а и b с вероятностями, соответственно, 0,75 и 0,25. Сравнить избыточность кода Хаффмана при алфавитном и блочном двухбуквенном кодировании. При алфавитном кодировании:
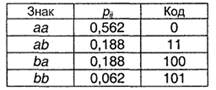
I(А) =0,811, К(А,2) = 1, Q(A,2) = 0,233 При блочном двухбуквенном кодировании (очевидно, pij=pi∙pj):
I(A) = 1,623 (в пересчете на 1 знак - 0,811), К(А,2) = 1,688 (в пересчете на знак - 0,844), Q(A,2) =0,040. Таким образом, блочное кодирование обеспечивает построение более оптимального кода, чем алфавитное. При использовании блоков большей длины (трехбуквенных и более) избыточность стремится к 0 в полном соответствии с первой теоремой Шеннона. Контрольные вопросы и задания 1. Приведите примеры обратимого и необратимого кодирования помимо рассмотренных в тексте. 2. В чем смысл первой теоремы Шеннона для кодирования? 3. Первичный алфавит содержит 8 знаков с вероятностями: "пробел" -0,25; "?" - 0,18; "&" - 0,15; "*" - 0,12; "+" - 0,1; "%" - 0,08; "!" - 0,07 и "!" - 0,05. В соответствии с правилами, изложенными в п.3.2.1, предложите вариант неравномерного алфавитного двоичного кода с разделителем знаков, а также постройте коды Шеннона-Фано и Хаффмана; сравните их избыточности. 4. Постройте в виде блок-схемы последовательность действий устройства, производящего декодирование сообщения, коды которого удовлетворяют условию Фано. Реализуйте программно на каком-либо языке программирования. 5. Является ли кодирование по методу Шеннона-Фано и по методу Хаффмана однозначным? Докажите на примере алфавита А, описанного в п.3.2.1. 6. С помощью электронных таблиц проверьте правильность данных о средней длине кода К(А,2) для всех обсуждавшихся в п.3.2.1. примерах неравномерного алфавитного кодирования. 7. Продолжите пример 3.2, определив избыточность при трехбуквенном блочном кодировании. 8. Для алфавита, описанного в задаче 3, постройте вариант минимального кода Бодо. 9. Проверьте данные об избыточность кода Бодо для русского и английских языков, приведенных в п.3.2.2. Почему избыточность кода для русского языка меньше? 10. Почему в 1 байте содержится 8 бит? 11. Оцените, какое количество книг объемом 200 страниц может поместиться:
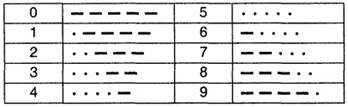
12. Почему в компьютерных устройствах используется байтовое кодирование? 13. Что такое "лексикографический порядок кодов"? Чем он удобен? 14. Для цифр придумайте вариант байтового кодирования. Реализуйте процедуру кодирования программно (ввод - последовательность цифр; вывод - последовательность двоичных кодов в соответствии с разработанной кодовой таблицей). 15. Разработайте программу декодирования байтовых кодов из задачи 13. 16. Код Морзе для цифр следующий:
17. Считая алфавит цифр самостоятельным, а появление различных цифр равновероятным, найдите избыточность кода Морзе для цифрового алфавита. В лексиконе "людоедки" Эллочки Щукиной из романа Ильфа и Петрова "12 стульев" было 17 словосочетаний ("Хо-хо!", "Ого!", "Блеск!", "Шутишь, парниша", "У вас вся спина белая" и пр.). (a) Определите длину кода при равномерном словесном кодировании. (b) Предложите вариант равномерного кодирования данного словарного запаса. Глава 6. Кодирование Вопросы кодирования издавна играли заметную роль в математике.
Пример
Ранее средства кодирования играли вспомогательную роль и не рассматривались как отдельный предмет математического изучения, но с появлением компьютеров ситуация радикально изменилась. Кодирование буквально пронизывает информационные технологии и является центральным вопросом при решении самых разных (практически всех) задач программирования:
ЗАМЕЧАНИЕ Само составление текста программы часто и совершенно справедливо называют кодированием.
Не ограничивая общности, задачу кодирования можно сформулировать следующим образом. Пусть заданы алфавиты Если |B|=m, то F называется m-ичным кодированием. Наиболее распространенный случай B={0, 1} – двоичное кодирование. Именно этот случай рассматривается в последующих разделах; слово «двоичное» опускается. Типичная задача теории кодирования формулируется следующим образом: при заданных алфавитах А, В и множестве сообщений S найти такой кодирование F, которое обладает определенными свойствами (то есть удовлетворяет заданным ограничениям) и оптимально в некотором смысле. Критерии оптимальности, как правило, связан с минимизацией длин кодов. Свойства, которые требуются от кодирования, бывают само разнообразной природы: · существование декодирования – это очень естественное свойство, однако даже оно требуется не всегда. Например, трансляция программы на языке высокого уровня в машинные команды – это кодирование, для которого не требуется однозначного декодирования; · помехоустойчивость, или исправление ошибок: функция декодирования F-1 обладает таким свойством, что · заданная сложность (или простота) кодирования и декодирования. Например, в криптографии изучаются такие способы кодирования, при которых имеется просто вычисляемая функция F, но определение функции F-1 требует очень сложных вычислений. Большое значения для задач кодирования имеет природа множества сообщений S. При одних и тех же алфавитах А, В и требуемых свойствах кодирования F оптимальные решения могут кардинально отличаться для разных S. Для описания множества S (как правило, очень большого или бесконечного) применяются различные методы: · теоретико –множественное описание, например · вероятностное описание, например S=A*, и заданы вероятности pi появления букв в сообщении, · логико-комбинаторное описание, например, S задано порождающей формальной грамматикой. Алфавитное кодирование Кодирование F может сопоставлять код всему сообщению из множества S как единому целому или же строить код сообщения из кодов его частей. Элементарной частью сообщения является одна буква алфавита А. Этот простейший случай рассматривается в этом и следующих двух разделах.
Префикс и постфикс слова Пусть задано конечное множество Пустое слово обозначается Если Таблица кодов Алфавитное (или побуквенное) кодирование задается схемой (или таблицей кодов)
Множество кодов букв V :=
Пример Рассмотрим алфавиты A:={0,1,2,3,4,5,6,7,8,9}, B:={0,1} и схему
Эта схема однозначна, но кодирование не является взаимно однозначным:
А значит, невозможно декодирование. С другой стороны, схема
Известная под названием «двоично-десятичное кодирование», допускает однозначное декодирование. Разделимые схемы Рассмотрим схему алфавитного кодирования
То есть любое слово, составленное из элементарных кодов, единственным образом разлагается на элементарные коды. Алфавитное кодирование с разделимой схемой допускает декодирование. Если таблица кодов содержит одинаковые элементарные коды, то есть если
где
Префиксные схемы Схема
ТЕОРЕМАПрефиксная схема является разделимой. Доказательство От противного. Пусть кодирование со схемой
Поскольку
ЗАМЕЧАНИЕ Свойство быть префиксной является достаточным, но не является необходимым для разделимости схемы.
Пример Разделимая, но не префиксная схема:
Неравенства Макмиллана Чтобы схема алфавитного кодирования была разделимой, необходимо, чтобы длины элементарных кодов удовлетворяли определенному соотношению, известному как неравенство Макмиллана.
ТЕОРЕМАЕсли схема Доказательство Обозначим
Раскрывая скобки, имеем сумму
где i1...in – различные наборы номеров элементарных кодов. Обозначим через
Каждому слагаемому вида ( Таким образом,
Следовательно,
Неравенство Макмиллана является не только необходимым, но и в некотором смысле достаточным условием разделимости схемы алфавитного кодирования. ТЕОРЕМАЕсли числа l1…ln удовлетворяет неравенству то существует разделимая схема алфавитного кодирования Доказательство Без ограничений общности можно считать, что Пусть
Тогда неравенство Макмиллана можно записать так:
Из этого неравенства следуют m неравенств для частичных сумм:
Рассмотрим слова длины Пример Азбука Морзе – это схема алфавитного кодирования <A H O V где по историческим и техническим причинам 0 называется точкой и обозначается знаком «.», а 1 называется тире и обозначается знаком «-». Имеем: ¼+1/16+1/16+1/8+½+1/16+1/8+1/16+¼+1/16+ 1/8+1/16+1/4+1/4+1/8+1/16+1/16+1/8+1/8+ ½+1/8+1/16+1/8+1/16+1/16+1/16 = = 2/2 + 4/4 + 7/8 + 12/16 = 3+5/8 > 1. Таким образом, неравенство Макмиллана для азбуки Морзе не выполнено, и эта схема не является разделимой. На самом деле в азбуке Морзе имеются дополнительные элементы – паузы между буквами (и словами), которые позволяют декодировать сообщения. Эти дополнительные элементы определены неформально, поэтому прием и передача сообщений с помощью азбуки Морзе, особенно с высокой скоростью, является некоторым искусством, а не простой технической процедурой.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,  и функция
и функция 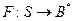 , где S – некоторое множество слов в алфавите А, S
, где S – некоторое множество слов в алфавите А, S 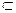 A*. Тогда функция F называется кодированием, элементы множества S – сообщениями, а элементы
A*. Тогда функция F называется кодированием, элементы множества S – сообщениями, а элементы 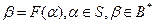 - кодами (соответствующих сообщений). Обратная функция F-1 (если она существует!) называется декодированием.
- кодами (соответствующих сообщений). Обратная функция F-1 (если она существует!) называется декодированием.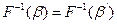 , если
, если 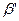 в определенном смысле близко к
в определенном смысле близко к  .
. ;
; ;
;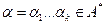 , то количество букв в слове называется длиной слова:
, то количество букв в слове называется длиной слова: 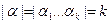 .
. .
.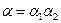 , то
, то  называется началом, или префиксом, слова
называется началом, или префиксом, слова 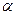 , а
, а 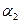 - окончанием, или постфиксом, слова
- окончанием, или постфиксом, слова  (соответственно,
(соответственно, 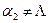 ), то
), то  :
:
 называется множеством элементарных кодов. Алфавитное кодирование пригодно для любого множества сообщений S:
называется множеством элементарных кодов. Алфавитное кодирование пригодно для любого множества сообщений S:
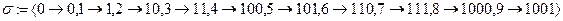
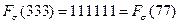 ,
,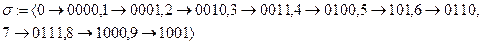
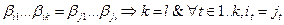 ,
,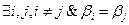
 , то схема заведомо не является разделимой. Такие схемы далее не рассматриваются, то есть
, то схема заведомо не является разделимой. Такие схемы далее не рассматриваются, то есть
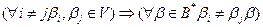
 , что
, что
 , значит,
, значит,  , но это противоречит тому, что схема префиксная.
, но это противоречит тому, что схема префиксная.
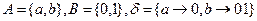 .
.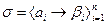 разделима, то
разделима, то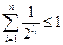 , где
, где 
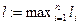 . Рассмотрим n-ю степень левой части неравенства
. Рассмотрим n-ю степень левой части неравенства .
.
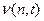 количество входящих в эту сумму слагаемых вида 1/2t, где t=li1+…+lin. Для некоторых t может быть, что
количество входящих в эту сумму слагаемых вида 1/2t, где t=li1+…+lin. Для некоторых t может быть, что 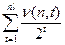 .
.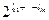 )-1можно однозначно сопоставить код (слово в алфавите B) вида
)-1можно однозначно сопоставить код (слово в алфавите B) вида 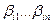 . Это слово состоит из n элементарных кодов и имеет длину t.
. Это слово состоит из n элементарных кодов и имеет длину t.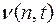 - это число некоторых слов вида
- это число некоторых слов вида 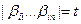 . В силу разделимости схемы
. В силу разделимости схемы 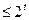 , в противном случае заведомо существовали бы два одинаковых слова
, в противном случае заведомо существовали бы два одинаковых слова 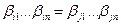 , допускающих различное разложение. Имеем
, допускающих различное разложение. Имеем
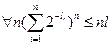 , и значит
, и значит 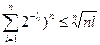 , откуда
, откуда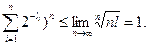
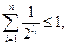
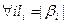
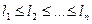 . Разобьем множество {l1,…,ln} на классы эквивалентности по равенству {L1,…,Lm}, m
. Разобьем множество {l1,…,ln} на классы эквивалентности по равенству {L1,…,Lm}, m 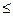 n.
n.

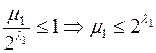
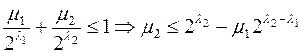
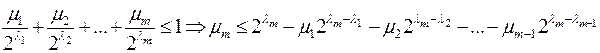
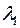 в алфавите В. Поскольку
в алфавите В. Поскольку 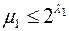 , из этих слов можно выбрать
, из этих слов можно выбрать 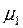 различных слов
различных слов 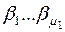 длины
длины 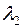 и не начинающихся со слов
и не начинающихся со слов 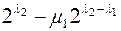 . Но
. Но 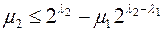 , значит, можно выбрать
, значит, можно выбрать  различных слов. Обозначим их
различных слов. Обозначим их 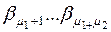 . Исключим слова, начинающиеся с
. Исключим слова, начинающиеся с 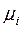 слов длины
слов длины  ,
, 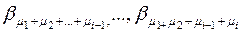 , причем эти слова не будут начинаться с тех слов, которые были выбраны раньше. В то же время длины этих слов все время растут (так как
, причем эти слова не будут начинаться с тех слов, которые были выбраны раньше. В то же время длины этих слов все время растут (так как 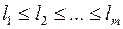 ), поэтому они не могут быть префиксами тех слов, которые выбраны раньше. Итак, в конце имеем набор из n слов
), поэтому они не могут быть префиксами тех слов, которые выбраны раньше. Итак, в конце имеем набор из n слов  , коды
, коды  не являются префиксами друг друга, а значит, схема
не являются префиксами друг друга, а значит, схема 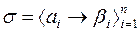 будет префиксной и, по теореме предыдущего подраздела, разделимой.
будет префиксной и, по теореме предыдущего подраздела, разделимой.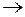 01,B
01,B