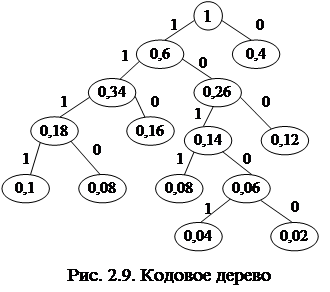|
|
Построение алгоритма кодирования.Имея данную систему уравнений, на роль избыточных разрядов следует выбирать те, которые встречаются в проверочных равенствах по одному разу, т.е. а3, a4, a5. Выделение избыточных разрядов сопровождается определением информационных разрядов помехоустойчивого кодового слова. При этом для данного кода будут получены правила кодирования
a4 = a1 Å a2 Å a7 a5 = a2 Å a6 Å a7 2.2.2. Процесс кодирования и декодирования
1 1 0 1 1 1 0 0 1 0 1 1 1 0 0 1 1 1 1 1 0 1 4 3 2 1 7 6 5 4 3 2 1 7 6 5 4 3 2 1 4 3 2 1 Кодирование:
а7 а6 а5 а4 а3 а2 а1 а3 = 1 Å 1 Å 1 = 1 а4 = 1 Å 0 Å 1 = 0 а5 = 0 Å 1 Å 1 = 0 Искажение помехой: Å 0000010 - вектор ошибки 1100111 - запрещенное кодовое слово Декодирование: - вычисление опознавателя ошибки: 1 Å 1 Å 1 Å 1 = 0 (первый разряд опознавателя) 1 Å 0 Å 1 Å 1 = 1 (второй разряд опознавателя) 1 Å 1 Å 0 Å 1 = 1 (третий разряд опознавателя), По таблице опознавателей отыскивается соответствующий опознавателю 110 вектор ошибки 0000010; - исправление ошибки (восстановление кодового слова ) 1100111 (запрещенное слово) Å 0000010 (вектор ошибки) 1100101 (разрешенное слово); - выделение содержимого информационных разрядов (а1, а2, а6, а7). На выходе декодера - 1101. Контрольные вопросы к пп. 2.1. и 2.2
1. Цель и суть любого кодирования. 2. Цели кодирования в технических системах. 3. Какая система счисления используется при построении простой и надежной аппаратуры? 4. Классификация помехоустойчивых кодов. 5. Цель помехоустойчивого кодирования. 6. Идея помехоустойчивого кодирования. 7. Варианты передачи кодового слова от шифратора к дешифратору и числа разных вариантов передач. 8. Что такое избыточная информация любого помехоустойчивого кода, для “кого” она таковой является и “кем” она формируется? 9. Какой по сути является избыточная информация у любого разделимого кода? 10. Какой по сути является избыточная информация у любого группового кода? 11. Какой по сути является избыточная информация у данного группового кода? 12. Чем представлена избыточная информация в кодовом слове любого помехоустойчивого кода? 13. Чем представлена избыточная информация в кодовом слове любого разделимого кода? 14. Чем представлена избыточная информация в кодовом слове любого группового кода? 15. Чем представлена избыточная информация в любом кодовом слове данного группового кода? 16. Чем представлена избыточная информация в конкретном кодовом слове данного группового кода? 17. Понятие хэммингового (кодового) расстояния (пояснить примером). 18. Понятие минимального хэммингового расстояния. 19. Минимальное хэммингово расстояние для кодов, которые только обнаруживают ошибки кратности r (пояснить геометрически, примером разрешенных слов, взятых из множества трехразрядных кодовых слов). 20. Минимальное хэммингово расстояние для кодов, которые только исправляют ошибки кратности S (пояснить геометрически, примером разрешенных слов, взятых из множества трехразрядных кодовых слов). 21. Минимальное хэммингово расстояния для кодов, которые только обнаруживают ошибки кратности r и исправляют ошибки кратности S. 22. Построить множество n-разрядных кодовых слов с минимальным хэмминговым расстоянием, равным dmin. 23. Способы разбиения всего множества запрещенных кодовых слов на непересекающиеся подмножества; числа всех кодовых слов, запрещенных и разрешенных слов, непересекающихся подмножеств. 24. Понятие класса смежности. 25. Что такое опознаватель или синдром ошибки? 26. Как соотносятся между собой число классов смежности и количество исправляемых ошибок (пояснить словами и формулой)? 27. Как определяется число информационных, избыточных разрядов и разрядов опознавателей ошибок? 28. Как определить абсолютную и относительную избыточность кода? 29. Понятие оптимального помехоустойчивого кода. 30. Типы (модели) помех. Какие из них используются на лабораторных занятиях? 31. Что такое корректирующая способность кода? 32. Граница Хэмминга для существования оптимального корректирующего кода (понятие и формула). 33. Ограничение при выборе способа разбиения множества запрещенных слов на непересекающиеся подмножества, используемого для построения кода. 34. Алгоритм работы кодера группового кода и его устройство. 35. Алгоритм работы дешифратора группового кода и его устройство. 36. Как организована работа кодера без выполнения вычислительных операций алгоритма кодирования? 37. Как организована работа дешифратора, реализующего процедуру «максимум правдоподобия»? ЭФФЕКТИВНОЕ КОДИРОВАНИЕ Под информацией Р. Хартли понимал логическую инструкцию для дихотомического выбора и поиска данного сообщения или состояния из некоторого множества. Заметим, что дихотомия - это последовательное деление целого на две части, затем каждой части еще на две и т.д. При этом количество информации (по Хартли)определяется в виде J = log2N, где N - число различных состояний наблюдаемого объекта или размер алфавита сообщений источника; J - количество информации в битах. Если N = 2, то Jmin = 1 бит. При такой процедуре (программе) идентификации еще до восприятия сообщений все их множество в памяти приемника должно быть разбито на пары подмножеств (вплоть до отдельных элементов), образуя бинарное дерево. Если двигаться от вершины дерева к месту расположения в памяти искомого элемента, то можно наметить путь движения к данному сообщению, в котором повороты направо обозначим ²1², а повороты налево - ²0². Такой путь - это и есть информация для поиска данного сообщения в памяти приемника. Таким образом, информация (по Хартли) - это процедура (программа) дихотомического поиска; она представлена последовательностью команд или инструкций вида: ²направо², ²налево² или с учетом обозначений ²1², ²0². Заметим, что поиск объектов можно осуществлять различными процедурами в зависимости от наличия априорной (заранее известной приемнику) информации о них: - простым перебором или сканированием; - случайным выбором; - оптимальным поиском; - комбинированным поиском. Оптимальная процедура поиска - это процедура, обеспечивающая минимальное среднее количество команд для поиска данного объекта. Приемник в этом случае не опознает, каким по существу является принятое сообщение, а идентифицирует (отождествляет) принятое сообщение с одним из имеющихся в его памяти. Пусть имеется восемь различных сообщений, которые в памяти приемника упорядочены, как это указано на рис. 2.4. Оптимальная программа поиска объекта - сообщения ²Æ² имеет вид ²101². Из рисунка видно, что это кратчайший путь поиска.
0 1 2 3 4 5 6 7
Таким же образом можно обозначить все восемь сообщений; программы их поиска окажутся закодированы 3-х разрядными двоичными числами. Количество информации в каждой программе, определенное по формуле Р. Хартли, равно трём битам: J = log2 8 = 3 бит. Длина программы для выбора при таком равном разбиении совпадает с количеством информации. При данной схеме моделью источника сообщений является источник случайных сообщений. В мере информации Хартли неявно предполагается, что эти сообщения равновероятны. Однако на самом деле от источника поступают неслучайные последовательности, сообщения в которых обычно имеют разные вероятности. В данной схеме идентификации приемник в своей памяти имеет только алфавит состояний; он не способен запоминать даже один предыдущий элемент. Приемник воспринимает сообщения как статистически независимые и равновероятные состояния. Пусть известные приемнику вероятности сообщений различны и размещены в его памяти по убыванию. Все множество сообщений разбито без перемешивания на два равных по суммарным вероятностям подмножества. Сообщение, находящееся в правом подмножестве, находится командой ²вправо² или ²1², иначе - командой ²влево² или ²0². Каждое подмножество, в свою очередь, без перемешивания поделено на два и имеет такие же команды для выбора. Такое разбиение с назначением команд для выбора выполнено вплоть до отдельного элемента.
iu R t µ U v n l
Рис. 2.5. Оптимальный дихотомический поиск сообщений с равными вероятностями появления: i – сообщения; Pi – вероятность i - го сообщения.
Как видно из рис. 2.5, длина инструкции для дихотомического поиска в этом случае различна. Для поиска в памяти приемника самых частых сообщений с вероятностью 1/4 требуются всего две команды. Длина программы идентификации самых редких сообщений с вероятностью 1/16 состоит из четырех команд. Средняя длина программ поиска определяется в виде
В данном примере с ²идеальным² распределением вероятностей величина средней длины программ идентификации совпадает с количеством информации (2,75 бит), вычисляемым по формуле К. Шеннона:
где J - количество информации, H - энтропия источника сообщений. Для случая равновероятных сообщений , когда Энтропия является характеристикой информационной способности или мерой неопределенности состояния источника, так как представляет среднюю неожиданность его сообщений. При этом предполагается, что более неожиданные (редкие) сообщения - более информативны и наоборот. Энтропия имеет следующие свойства: 1) H = Hmax, если вероятности всех сообщений равны; 2) Hmax = log2 N, если H = 0, если одно из состояний источника достоверно; H = 0, если Pi = 1; 3) энтропия нескольких (в количестве k) статистически независимых источников равна сумме их энтропий:
4) энтропия простейшего источника двух разных сообщений определяется в виде H = -[P · log2 P + (1 - P) · log2(1 - P)], где P и (1 - P)- вероятности сообщений. Как видно, это функция одной переменной и может быть изображена графиком (рис. 2.6).
Рис. 2.6. Функции энтропии и неожиданности: H - энтропия простейшего источника; H1 - неожиданность его первого состояния
В начальный момент времени энтропия (неопределенность состояния) источника сообщений максимальна, так как информация еще не получена приемником. После завершения передачи сообщений энтропия источника равна нулю, а количество принятой информации на приемной стороне равно максимальной энтропии источника сообщений в начальный момент времени. Образно говоря, энтропия источника сообщений ²перетекает² в информацию для приемника. Этим объясняется равенство количества информации J и энтропии H в формуле К. Шеннона (несмотря на разную суть этих понятий). Целью эффективного кодирования является представление массивов сообщений с размером алфавита М компактными текстами, которые записаны кодовыми словами, составленными из символов алфавита меньшей мощности: m<M. Критерием эффективности оптимального кода является средняя длина кодового слова, определяемая в виде:
где Pi - вероятность появления данного кодового слова; li - длина кодового слова i-го сообщения; M - количество разных кодовых слов (размер алфавита сообщений). Идея сжатия текста состоит в том, что наиболее частые сообщения кодируются короткими словами, а более редкие - длинными. При этом средняя длина кодового слова будет минимальна. Заметим, что и в естественных языках наиболее частые слова - короткие, а редкие - длинные. При сжатии информации желательно обходиться без пробелов между словами, так как они удлиняют текст. Для этого кодовые слова необходимо строить так, чтобы более длинные из них не начинались с символов более коротких. В таком случае возможна однозначная дешифрация текста, если известно начало текста, в нем нет пробелов и искажений помехами. Иначе ошибочное чтение ²первого² или ²очередного²слова начинается не с присущей ему позиции и распространяется обычно на несколько последующих слов. Такое неоднократно возобновляющееся чтение называется треком ошибки. Учитывая статистические свойства источника сообщения, можно минимизировать среднее число двоичных символов, требующихся для отображения одного сообщения, что, при отсутствии шума, позволяет уменьшить время передачи или необходимую емкость массива данных. Эффективное кодирование для неравновероятных сообщений основано на теореме Клода Шеннона для дискретного канала без шума. Шеннон доказал, что последовательность сообщений некоторого алфавита можно закодировать так, что среднее число двоичных символов на одно сообщение будет сколь угодно близко к энтропии источника этих сообщений, но не меньше этой величины, т.е. (для m = 2, L ³ H). L ≥ H / log2 m Теорема Шеннона не указывает конкретного способа кодирования , но из нее следует, что при построении эффективного кода необходимо стремиться к тому, чтобы каждый двоичный символ кодовой комбинации нес максимальное количество информации. А для этого каждый символ ²0² или ²1² должен быть по возможности равновероятным и не зависимым от предыдущих символов. При идеальном распределении вероятностей кодируемых сообщений
При m = 2 такие идеальные вероятности кратны 2, а L = H. Примеры с такими вероятностями сообщений рассмотрены выше. Однако в реальной ситуации обычно вероятности сообщений не кратны 2. При этом не удается разбивать упорядоченные по убыванию вероятностей сообщения на буквально равные по суммарным вероятностям подмножества и на каждом шаге идентификации сообщения (когда нужно выбрать одно из двух подмножеств) выбор будет уже не оптимален и средняя длина кодового слова будет больше, чем энтропия (в отличие от случая, где вероятности сообщений кратны 2). Однако если оказывается, что избыточность построенного кода невелика, то он принимается для эксплуатации, иначе следует построить другой код. Абсолютная избыточность эффективного кода определяется разностью средней длины кодового слова и энтропии , т.е. в виде ∆L = Lср. - H. По существу Шеннон доказал теорему существования границы оптимальных кодов, которая задана в виде: Lmin= H / log2 m (для m = 2, Lmin = H). В случаях, когда избыточность кода большая, можно приблизиться к границе, т.е. сделать Lср. ≈ H, если кодировать в исходной последовательности не отдельные сообщения, а группы сообщений - блоки. Чем длиннее блоки, тем эффективнее код. Заметим, что дополнительный эффект сжатия информации получается здесь не за счет того, что учитываются более дальние статистические связи. Этот эффект достигается тем, что алфавит исходных сообщений в количестве М заменяется большим набором макросообщений или блоков в количестве MK , где K - длина блока. Такой набор удается точнее разбить на близкие по суммарным вероятностям подмножества. В пределе, при K®¥, вероятности появления этих блоков становятся одинаковыми, так как они встречаются в последовательности по одному разу, и мы приходим к ситуации, описанной Р. Хартли. В этом случае для идентификации любого блока требуются программы одинаковой длины (кодовые слова одинаковой длины). Для сравнения эффективности разных кодов, кодирующих отдельные сообщения или блоки из К сообщений, следует использовать приведенную меру Lср. = L ср. бл. / K , так как для кодирования блока из К сообщений требуется, очевидно, более длинное слово, чем для отдельного сообщения. Основной эффект сжатия информации получается за счет того, что более частые сообщения кодируются короткими словами, а редкие - длинными, так что средняя длина кодового слова получается минимальной. Дополнительный эффект сжатия получается за счет устранения пробелов между словами оптимального кода. При этом более длинные кодовые слова строятся таким образом, что не начинаются с символов коротких. Однако очевидны ситуации, когда на вход приемника поступают статистически зависимые сообщения. Реальные тексты, файлы - это последовательности вовсе не случайных сообщений. Однако оптимальный код предназначен для кодирования только статистически независимых сообщений. В отмеченных ситуациях требуется предварительно осуществлять декорреляцию последовательности сообщений. Для этого есть два способа: - декорреляция блоками; - декорреляция L-граммами (более эффективна). При первом способе не удается учесть статистические связи на границах между блоками. Это устраняется при кодировании L-граммами. При декорреляции любым способом исходный текст заменяется другим текстом , который записан макросимволами - блоками. Этот новый текст состоит из статистически малозависимых сообщений и кодируется обычным способом. Рассмотрим декорреляцию (сегментацию) и кодирование блоками по 4 сообщения следующей фразы: ² Пусть имеется информация... ² ®
Пусть имеется информация
0010 10 11 010 011 00110
Если n - длина исходной последовательности, k - длина блока, то число заменяющих ее блоков Nбл. = n / k. Декорреляция и кодирование L-граммами по 4 сообщения имеет вид:
11
Число L-грамм (по к сообщений), заменяющих исходную последовательность длиной n сообщений определяется в виде Nбл= n - (k - 1). Специфика технической реализации оптимального кодирования обусловлена тем, что кодовые слова имеют разную длину. Если кодовые слова передаются по каналу связи через равные интервалы времени Dt или размещаются в памяти машины , то будут появляться интервалы Dti между словами, когда канал не занят сообщениями, а в ячейках памяти - незаполненные разряды (как это показано в табл. 2.4 и на рис. 2.7).
n = 8
Для эффективной передачи сообщений по каналу и при заполнении массива данных в памяти нужно установить буферное запоминающее устройство - БЗУ (накопитель) с числом разрядов не меньше удвоенного числа разрядов самого длинного кодового слова. Из этого накопителя в канал связи выдаются не отдельные кодовые слова, а непрерывная последовательность ²1² и ²0² с постоянной скоростью и без пробелов. При записи в ячейки памяти на выходе накопителя формируются слова одинаковой длины по числу разрядов в них. Соответственно при считывании данных из массива или для выделения кодовых слов нужен еще один такой же накопитель. Если кодирование осуществляется блоками или L-граммами, то на стороне источника сигналов необходим формирователь блоков или L-грамм, а на стороне приемника сообщений - их распознаватель (расформирователь). На рис. 2.8 представлена полная структурная схема системы эффективного кодирования, передачи и декодирования сообщений.
Методы построения эффективных кодов были впервые разработаны Шенноном и Фэно и существенно не различаются, поэтому соответствующий код получил название кода Шеннона-Фэно. Исходные данные для построения кода - это алфавит сообщений и их вероятности. Код строится следующим образом: все множество сообщений с их вероятностями выписывается в таблицу в порядке убывания вероятностей. Затем все множество разбивается на два подмножества так, чтобы суммы вероятностей в каждом из них были по возможности одинаковы. Всем сообщениям подмножества с наиболее вероятными сообщениями в качестве первого символа их кодовых слов приписывается ²0², а всем сообщениям второго подмножества назначается ²1². Каждое из подмножеств, в свою очередь, аналогично разбивается (без перемещения !) на два меньших подмножества, обозначается собственно ²0² или ²1² и т.д. Такой процесс повторяется до тех пор, пока в каждом подмножестве не останется по одному сообщению. Примечание: При кодировании блоками или L-граммами кодирование осуществляется точно так же; только в этом случае исходными данными для построения кода являются частоты (в пределе вероятности) блоков или L-грамм.
При построении кода Шеннона-Фэно оказываются возможными неоднозначные разбиения и при этом можно построить несколько разных кодов. Лучше использовать тот код, который имеет минимальную среднюю длину из всех других вариантов кодов. Для этого нужно построить множество различных вариантов и выбрать лучший. Хаффмен предложил такую процедуру построения эффективного кода, которая сразу дает наилучший вариант. Этапы этой процедуры следующие: 1) строится таблица, число столбцов в которой на один больше, чем размер алфавита сообщений; во второй столбец вписываются по убыванию вероятности, а в первый - соответствующие сообщения; 2) вероятности двух самых редких сообщений суммируются, образуя вероятность дополнительного псевдосообщения; 3) вероятности сообщений из 2-го столбца, кроме двух самых редких, вместе с псевдосообщением переписываются в порядке убывания частот в 3-й столбец справа; 4) действия (2) и (3) выполняются до тех пор, пока не образуется в последнем столбце псевдосообщение с вероятностью ²1²; при этом переупорядочиваются сообщения и псевдосообщения из 3-го, 4-го и т.д. столбцов. Далее для построения кодовых слов необходимо проследить все переходы данного сообщения по строкам и столбцам полученной диагональной матрицы и соответственно каждый переход закодировать символами ²0² или ²1².
Для наглядности сопоставления отдельным сообщениям соответствующих им кодовых слов строится бинарное кодовое дерево, в вершине которого размещается псевдосообщение с вероятностью 1. От вершины этого дерева опускаются две ветви, которые оканчиваются псевдосообщениями, полученными на предпоследнем шаге построения таблицы. Ветвь сообщения с большей вероятностью кодируется символом ²1², а с меньшей - ²0². Такое дихотомическое ветвление дерева продолжается до тех пор, пока не дойдем до вероятности каждого сообщения. Теперь, двигаясь по кодовому дереву сверху вниз, можно записать для каждого сообщения соответствующее ему кодовое слово. На рис. 2.9 представлено кодовое дерево и эффективный код в виде кодирующей таблицы (табл. 2.7) для восьми сообщений.
Контрольные вопросы к п. 2.3
1. Цель и суть любого кодирования в технических системах. 2. Конкретные цели кодирования в технических системах. 3. Цель эффективного (оптимального) кодирования. 4. Задача эффективного кодирования. 5. Основная идея эффективного кодирования. 6. Показатель эффективности оптимального кода; избыточность такого кода. 7. Определение понятия “информация” по Р. Хартли. 8. Определение понятия “энтропия”. 9. Величина энтропии источника случайных сообщений; свойства энтропии. 10. Энтропия и количество информации по К. Шеннону и Р. Хартли. 11. Связь энтропии источника с количеством информации у приемника. 12. Содержание теоремы К. Шеннона об оптимальном кодировании; граница существования для оптимальных кодов. 13. Способы декорреляции последовательности сообщений. 14. Особенности реализации систем оптимального кодирования. 15. Процедуры построения оптимальных кодов. 16. Особенности строения кодовых слов эффективного кода. 17. Каким образом можно осуществить защиту кодовых слов эффективного кода от помех? 18. Перечислите все факторы, за счет которых осуществляется эффект “сжатия” текста. СПИСОК ЛИТЕРАТУРЫ
1. Темников Ф.Е., Афонин В.А., Дмитриев В.И. Теоретические основы информационной техники: Учеб. пособие для студентов. – М.: Энергия, 1979. – 512 с. 2. Дмитриев В.И. Прикладная теория информации: Учеб. для студентов. – М.: Высш. шк., 1989. – 320 с. 3. Гуменюк А.С. Преобразование сообщений в цепи управления: Учеб. пособие для студентов. – Омск: Изд. ОмПИ, 1982. – 84 с. 4. Баранов Л.А. Квантование по уровню и временная дискретизация в цифровых системах управления. – М.: Энергоатомиздат, 1990. – 304 с. ОГЛАВЛЕНИЕ
1. Дискретизация сообщений……………………………………………………………4 1.1. Общие положения о дискретизации сообщений и представлении их функциями………………………………………………………………………... 4 1.2. Квантование сообщений по уровню…………………………………………….6 1.3. Временная дискретизация сообщений. Спектральное и импульсное представление сигналов…………………………………………………………14 2. Кодирование сообщений……………………………………………………………..22 2.1. Основные положения о кодировании сообщений……………………………..22 2.2. Помехоустойчивое кодирование………………………………………………..22 2.2.1. Процедура построения группового кода…………………………………30 2.2.2. Процесс кодирования и декодирования………………………………….32 2.3. Эффективное кодирование……………………………………………………...34 Список литературы……………………………………………………………………...45 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 а3 = a1 Å a6 Å a7
а3 = a1 Å a6 Å a7
 0 Х § ¨ º Æ ª #
0 Х § ¨ º Æ ª # Pi 1/4 1/4 1/8 1/8 1/16 1/16 1/16 1/16
Pi 1/4 1/4 1/8 1/8 1/16 1/16 1/16 1/16 элемента.
элемента. ,
, , эта формула принимает вид формулы Р. Хартли J = log2 N. Если неожиданность появления i-го сообщения определить в виде Hi = -log2 P, (как это предложил А. Реньи),то
, эта формула принимает вид формулы Р. Хартли J = log2 N. Если неожиданность появления i-го сообщения определить в виде Hi = -log2 P, (как это предложил А. Реньи),то 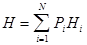 . Это позволяет пояснить суть понятия ²энтропия².
. Это позволяет пояснить суть понятия ²энтропия². .
. ;
;

 ,
, , L = H / log2 m
, L = H / log2 m
 ² Пусть имеется информация...²
² Пусть имеется информация...²

 U1
U1