
|
|
ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
Рассмотрим идею помехоустойчивого кодирования на примере кодирования сообщений словами равной длины, в которых фиксированы позиции информационных и дополнительных разрядов. Для этих целей используются так называемые равномерные разделимые блоковые коды. Кодирующее устройство (шифратор) осуществляет следующее преобразование над входным безызбыточным k-разрядным кодовым словом, которое несет только полезную информацию. Кодер наращивает длину слова, увеличивая число разрядов кодового слова до n > k , при этом появляются дополнительные (избыточные, проверочные или контрольные) разряды, кроме так называемых информационных (k) разрядов, несущих полезную информацию. Таким образом, кодовое слово на выходе кодера содержит n - k = m избыточных разрядов. Содержимое дополнительных (избыточных) разрядов кодер определяет в соответствии с алгоритмом кодирования на основе содержимого информационных разрядов. Избыточная информация в помехоустойчивом кодовом слове представлена содержимым определенных информационных и дополнительных разрядов. Сама же избыточная информация – это, по существу, алгоритм формирования избыточных разрядов, т.е. алгоритм кодирования, который известен дешифратору (декодеру). То есть для дешифратора данный алгоритм кодирования является избыточной информацией - это то постоянное преобразование, что сохраняется независимо от того, какие кодовые слова передаются от источника к приемнику. Используя эту избыточную информацию, дешифратор принимает очередное слово и проверяет содержимое всех его разрядов на соответствие данному алгоритму кодирования. Если данное слово не удовлетворяет используемому алгоритму кодирования, то дешифратор делает вывод об обнаружении ошибки и, в зависимости от того ²в какой степени² это соответствие не выполняется, может опознавать и исправлять некоторые ошибки. Кратко это можно выразить следующим образом: идея помехоустойчивого кодирования состоит во внесении кодером избыточной информации в виде алгоритма (правил) кодирования с помощью дополнительных разрядов помехоустойчивого кодового слова с последующей проверкой декодером этого слова на соответствие принятому алгоритму кодирования (рис. 2.1). Все множество помехоустойчивых кодов различается разнообразными алгоритмами кодирования, каждый из которых разработан для защиты кодовых слов от помех определенного характера и их кратности. Обычно различают помехи некоррелированные (при которых искажение слова в данном разряде не связано с искажением в других разрядах) и коррелированные или пакеты ошибок (при которых искажение в данном разряде приводит к искажению в других разрядах). Помехи различной интенсивности порождают ошибки разной кратности: однократные, 2-кратные и R-кратные, когда в кодовом слове меняется на противоположное (искажается) содержимое 1, 2,¼, R разрядов одновременно
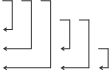
Никакие коды не могут не только исправлять, но и обнаруживать все ошибки. Это объясняется следующим. Пусть требуется закодировать двоичным кодом Q = 2k разных сообщений (Q - объем кода, k - число двоичных разрядов). Для каждого безызбыточного входного слова, отображающего конкретное сообщение, декодер должен сформировать на выходе только одно помехоустойчивое слово, поэтому разрешенных помехоустойчивых кодовых слов тоже 2k. Все множество n-разрядных кодовых слов имеет мощность 2n, из которых в подмножестве разрешенных кодовых слов только 2k. Помехоустойчивое слово на входе дешифратора может иметь искаженные разряды, поэтому все множество n -разрядных разных кодовых слов, которые могут иметь место на входе дешифратора, имеет мощность 2n. На множестве n -разрядных кодовых слов можно выделить, кроме подмножества разрешенных кодовых слов, подмножество запрещенных кодовых слов мощностью (2n - 2k). При построении помехоустойчивых кодов важно правильно использовать подмножество запрещенных кодовых слов. Это значит, что запрещенных кодовых слов должно быть как можно меньше, но их наличие должно позволять дешифратору исправлять как можно большее число разнообразных ошибок. При этом не пришлось бы сильно удлинять помехоустойчивое кодовое слово, в котором дополнительные и информационные разряды равно подвержены воздействию помех. Абсолютная избыточность кода определяется в виде m = n - k; Относительная избыточность Rn = (n - k)/n или Rk = (n - k)/ k. С учетом понятия избыточности кода легко определить понятие ²оптимальный помехоустойчивый код². Это такой код, который обеспечивает заданную корректирующую способность (обнаружение или исправление ошибок определенной кратности) минимальным числом дополнительных разрядов. Избыточные разряды могут быть искажены так же, как и информационные, поэтому, удлиняя слово дополнительными разрядами, мы снижаем его ²помехоустойчивость². Кодовое слово может передаваться от шифратора к дешифратору с ошибкой и без нее. Таким образом, возможны два варианта передачи кодового слова: правильная и неправильная. Число вариантов правильной передачи, когда разрешенное кодовое слово, проходя путь от кодера к декодеру, трансформируется само в себя, равно 2k. Существуют также два варианта неправильной передачи: 1) разрешенное кодовое слово на пути от кодера к декодеру трансформируется в иное разрешенное слово. В этих случаях декодер, проверяя структуру и содержимое принятого кодового слова на соответствие данному алгоритму кодирования, вынужден принять решение, что кодовое слово правильно. При этом дешифратор не только не исправит эту ошибку, но даже и не обнаружит ее. Так как каждое разрешенное слово может трансформироваться в любое другое разрешенное слово, то число вариантов такой передачи 2k(2k - 1). 2) разрешенное кодовое слово трансформируется в запрещенное. В таких случаях дешифратор способен обнаружить ошибку, а в некоторых – и исправить. Так как каждое разрешенное слово может трансформироваться в любое запрещенное слово (число которых 2n - 2k), то число вариантов такой ошибочной передачи 2k(2n - 2k). Суммируя числа разных вариантов передачи, получим общее число вариантов передачи 2k × 2n = 2k + 2k(2k - 1) + 2k(2n - 2k). На рис. 2.2 графически представлены разные варианты передачи кодовых слов.
- разрешенные слова; - запрещенные слова; - варианты правильной передачи; - варианты передачи с необнаруживаемой ошибкой; - варианты передачи с обнаруживаемой ошибкой.
Если в кодовых словах позиции избыточных и информационных разрядов фиксированы, то такой код называется разделимым; если позиции не фиксированы, то такой код называется неразделимым. При построении помехоустойчивого кода следует разумно использовать подмножество запрещенных кодовых слов. Есть два способа разбиения подмножества запрещенных кодовых слов на непересекающиеся подмножества. В зависимости от принятого способа разбиения возможно построение разных по сути помехоустойчивых кодов и соответственно два разных подмножества помехоустойчивых корректирующих кодов. И те, и другие коды могут обнаруживать и исправлять ошибки, но делают это по-разному. 1-й способ: разбиение всех запрещенных слов на непересекающиеся подмножества по принципу принадлежности (близости) запрещенного слова к разрешенному кодовому слову. При этом ²вокруг² каждого разрешенного кодового слова группируются такие запрещенные слова, которые ²ближе² к нему, чем к другим разрешенным словам (рис. 2.3). В этом случае в качестве разрешенных кодовых слов следует выбирать такие, которые составляют множество элементов, удаленных друг от друга на расстояние не меньше некоторой величины (называемой минимальным хэмминговым расстоянием).
При таком способе разбиения дешифратор выносит решение в пользу того разрешенного слова, расстояние от которого до принятого слова меньше, чем до других разрешенных слов. Количество непересекающихся подмножеств запрещенных кодовых слов при этом равно числу разрешенных слов 2k. 2 -й способ: разбиение по принципу принадлежности запрещенного кодового слова к вектору ошибки или к классу смежности. При таком разбиении декодер опознает не переданное ему слово, а вектор ошибки, которой оно оказалось поражено. Для этого декодер, учитывая содержимое избыточных и информационных разрядов, проверяет принятое слово на соответствие данному алгоритму кодирования и в результате вычисляет опознаватель (синдром) ошибки, который указывает на принадлежность принятого слова к одному из непересекающихся подмножеств запрещенных слов (классов смежности), ²порожденных² определенным вектором ошибки. В такой системе кодер должен по определенным правилам кодирования определять содержимое избыточных разрядов на основе известного содержимого информационных разрядов. Эти правила или алгоритм кодирования представляют собой систему уравнений, в которых данными (известными величинами) являются значения информационных разрядов. Для определения содержимого каждого избыточного разряда применяется свое уравнение. Дешифратор проверяет на истинность каждое из этих уравнений, проверка дает либо ²0², либо ²1². Проверки всех уравнений дают множество нулей и единиц, называемое опознавателем ошибки. Если опознаватель состоит только из одних нулей, декодер делает вывод об отсутствии ошибки, иначе, по виду ненулевого опознавателя, декодер может определить тип ошибки, так как опознаватель указывает на принадлежность принятого слова подмножеству запрещенных слов, порожденных данным вектором ошибки. Два способа разбиения запрещенных слов на непересекающиеся подмножества хорошо интерпретируются с помощью табл. 2.1, в ячейках которой размещены все n-разрядные запрещенные и разрешенные слова в количестве 2n. Следовательно, ²площадь² этой таблицы, измеренная числом ее элементов, также равна 2n. В первой строке таблицы размещаются только разрешенные слова, поэтому ее ширина (число столбцов) равна 2k , а число строк - 2n-k. В каждой другой строке размещаются запрещенные слова, образованные из разрешенных слов и соответствующего подлежащего исправлению вектора ошибок. Все строки, кроме первой, представляют непересекающиеся (по векторам ошибок) подмножества запрещенных кодовых слов, называемые классами смежности; их число равно 2n-k-1. Класс смежности - это подмножество запрещенных слов (в количестве 2k), порожденных одним вектором ошибки. В каждом столбце, начиная со второго элемента, размещается непересекающееся подмножество запрещенных слов (в количестве
Из табл. 2.1 видно, что число классов смежности равно 2n-k-1; а общее число всех n-разрядных слов 2n =2k · 2n-k. Коды, использующие или первое, или второе разбиение, способны обнаруживать и исправлять ошибки, но возникает вопрос: как выбирать корректирующие коды? На практике проблемы выбора нет. В тех случаях, когда разработчик знает векторы ошибок, которые могут нанести непоправимый ущерб системе, приходится строить корректирующий код на основе разбиения по принципу принадлежности к заданному вектору ошибки или классу смежности. Если такой опасности нет, то разработчик должен разрабатывать код, исправляющий более вероятные ошибки и обеспечивающий простую и надежную реализацию. Для определения степени различия между кодовыми словами вводится специальная метрика - кодовое или хэммингово расстояние. Расстояние между двумя кодовыми словами определяется числом разрядов с различным содержимым. Формально кодовое расстояние можно определить, подсчитав число единиц в кодовом слове, полученном поразрядным суммированием по модулю 2 сравниваемых кодовых слов. Пример: Å 01011101 Кодовое расстояние d=1+1=2. Минимальное хэммингово расстояние задает такое множество разрешенных слов, для любой пары в котором простое кодовое расстояние не меньше заданной величины. Хэмминг установил границу существования оптимальных корректирующих кодов. Пусть имеется возможность кодировать словами длиною n- разрядов. При этом все множество разных двоичных слов (включая запрещенные) составляет величину 2n. Требуется узнать, какое количество слов из этого множества можно использовать в качестве разрешенных, если необходимо исправлять все ошибки вплоть до S-кратных. Для того чтобы все ошибки названной кратности были исправляемы, в каждом из непересекающихся подмножеств данного разбиения число всех запрещенных слов должно быть не меньше числа ошибок, порождающих эти слова. Число возможных ошибок в n-разрядном кодовом слове: - однократных - - двукратных - - S-кратных - - общее число, включая S-кратные: Пример: Для множества трехразрядных слов {000, 001, 011, 100, 101, 110, 111 } dmin = 1 выберем те слова, для которых dmin = 2.
Это разрешенные слова для кода, обнаруживающего однократные ошибки. Если дешифратор принимает кодовое слово с нечетным числом единиц, то это значит, что произошла однократная ошибка. Выберем те слова, для которых dmin = 3.
Это разрешенные слова для кода, исправляющего однократные ошибки. Если дешифратор принимает слова: 100 или 010 или 001 или 000, то это значит, что передано 000; 011 или 101 или 110 или 111, то это значит, что передано 111.
Поскольку все ошибки исправить невозможно, то разработчик строит код в расчете на те ошибки, которые исправлять необходимо. В дальнейшем вектором ошибки будем называть двоичное псевдослово, содержащее ²1² в тех разрядах, содержимое которых искажено помехами в данном помехоустойчивом кодовом слове. Пример: 10111011 - помехоустойчивое разрешенное кодовое слово Å 00101000 - вектор ошибки 10010011 - запрещенное слово Множеству подлежащих исправлению векторов ошибок должно соответствовать множество запрещенных слов, порожденных из данного разрешенного слова этими ошибками. Таким образом, в каждом подмножестве столько запрещенных слов, сколько разных ошибок мы хотим исправить. Если требуется исправлять все ошибки кратности не более S , то количество запрещенных слов в каждом подмножестве, вместе с соответствующим разрешенным словом, равно
Таким образом, определяется граница Хэмминга для существования оптимальных корректирующих кодов. Пример:Пусть для построения кода, корректирующего все однократные ошибки, используются однобайтовые слова. Требуется определить максимальное число разрешенных слов, выбираемых из всего множества однобайтовых слов. Число однократных ошибок Максимальное число разрешенных слов Кодирование и декодирование на основе определенного алгоритма (правила) кодирования можно заменить табличным кодированием и декодированием. В этом случае необходимо заранее, до создания кодера и декодера, ²вычислить по алгоритму² все множество разрешенных и соответствующих им запрещенных слов. При этом в памяти кодера размещается кодирующая таблица, которая представляет взаимнооднозначное соответствие входных безызбыточных k-разрядных и помехоустойчивых n-разрядных слов. В памяти декодера размещается декодирующая таблица соответствия запрещенных слов определенным разрешенным. Алгоритм табличного кодирования (декодирования) сводится к поиску в первой колонке таблицы слова, тождественного входному. Идентификация входного слова завершается считыванием из соответствующей строки второй колонки выходного слова. Кодирование на основе кодирующих таблиц – самый распространенный способ кодирования. Рассмотрим для примера построение группового кода, корректирующего однократные ошибки. 2.2.1. Процедура построения группового кода Исходная информация для построения кода: - тип исправляемых ошибок – некоррелированные; - кратность исправляемых ошибок - S = 1; - объем кода (число кодируемых сообщений) - Q = 15. Процедура состоит из четырех этапов. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
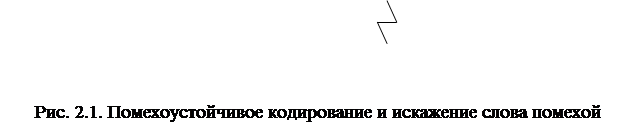


 ;
;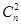 =
= 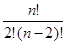 ;
; =
= 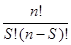 ;
; =
= 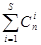 .
.
 000
000
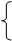 000
000 . Отношение числа всех n-разрядных слов к числу слов в каждом подмножестве определяет предельное количество непересекающихся подмножеств, а значит, - максимальное число разрешенных слов, т.е.
. Отношение числа всех n-разрядных слов к числу слов в каждом подмножестве определяет предельное количество непересекающихся подмножеств, а значит, - максимальное число разрешенных слов, т.е. ; если
; если 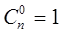 , то
, то 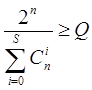 .
.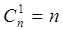 , т.е.
, т.е. 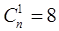 .
. , т.е. Q = 28.
, т.е. Q = 28.