
|
|
Синтаксические деревья. Построение вывода по дереву и наоборот.1. Синтаксические деревья. Дерево — это совокупность элементов, называемых узлами и отношений, образующих иерархическую структуру узлов. Один из узлов определен как корень. Рассмотрим предложение на английском языке «The big elephant ate the peanut». Его можно изобразить в виде следующей схемы:
Такая схема называется синтаксическимдеревом. Она описывает структуру предложения, разлагая его на составные части. Таким образом мы видим, что <предложение> состоит из <подлежащего> и <сказуемого>; <подлежащее> состоит из <артикля>, за которым следует <прилагательное>, за которым в свою очередь следует <существительное>. Для того чтобы описать структуру используются синтаксические единицы, которые заключаются в угловые скобки <> для того, чтобы отличить их от слов самого языка. 2. Построение вывода по дереву и наоборот. Рассмотрим следующую грамматику: Грамматика: <число> ::= <чс> <чс> ::= <чс><цифра>|<цифра> <цифра> ::= 0|…|9 Осуществим вывод предложения «22»:
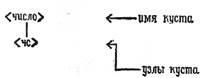
Чтобы указать первый непосредственный вывод, нарисуем куст начального символа <число>. Куст узла – это множество подчиненных ему узлов. Узлы куста образуют цепочку, которая заменяет имя куста в первом непосредственном выводе <число>=><чс>
Поступая таким же образом, строим по очереди 4 синтаксических диаграммы:
Таким образом мы построили синтаксическое дерево по выводу. Для синтаксических деревьев определена следующая терминология: Концевые узлы синтаксического дерева – это узлы, не имеющие подчиненного куста. На диаграмме это узлы 2 и 2. Концевой куст – это куст, все узлы которого концевые. На диаграмме два концевых куста с узлами 2 и 2. Также имеет место следующая терминология. Пусть N – узел дерева. Сыновьями N называют узлы куста, подчиненного N. N – их отец. Сыновья называются братьями, самым младшим является левый из них. К примеру, на диаграмме верхний узел <чс> является единственным сыном узла <число>. Он же имеет двух сыновей: <чс> и <цифра>. Поддерево синтаксического дерева состоит из узла дерева с той частью дерева, которая исходит из него.
Можно восстановить вывод по синтаксическому дереву при помощи обратного процесса: На диаграмме видно, что концевые узлы образуют цепочку 22. Самый правый концевой куст указывает непосредственный вывод: 2<цифра> => 22 Чтобы пройти по синтаксическому дереву до 2<цифра>, мы отсекаем куст от дерева – удаляем его (можно на доске стереть), производя непосредственную редукцию. Отсекая опять куст 2, получаем редукцию: <цифра> <цифра> => 2<цифра> => 22 Продолжая этот процесс, восстанавливаем вывод и отсекаем куст, указывающий на этот вывод. Подводя итог, можно сформулировать следующие положения о синтаксических деревьях:
будет иметь тоже синтаксическое дерево, что и было показано изначально
Определение. Предложение грамматики неоднозначно, если для его вывода существует более чем одно синтаксическое дерево. Грамматика неоднозначна, если она допускает неоднозначные предложения, в противном случае она однозначна. (Для себя: Пусть G[Z] – грамматика. Цепочка x будет являться сентенциальной формой, если x выводима из начального символа Z, т.е. если Z =>* x.) Если сентенциальная форма неоднозначна, то она имеет более чем одно синтаксическое дерево, и поэтому в общем случае больше чем одну основу. Рассмотрим следующую грамматику арифметических выражений, в которой используется единственный операнд в качестве идентификатора и бинарные операторы + и *: E::= E+E|E*E|i Сентенциальная форма i+i*i имеет две основы <E>+<E> и <E>*<E>. Если мы хотим разобрать эту сентенциальную форму, то неизвестно, с какой основы мы должны начать. Грамматика неоднозначна, и мы можем выбрать любую из основ. Таким образом, мы не можем сказать, что выполняется раньше: умножение или сложение. В итоге получаются два синтаксических дерева для данной сентенциальной формы.
Теперь рассмотрим следующую грамматику: <E> ::= <expr>|<E> + <expr>|<E> - <expr> <expr>::= <set>|<expr>+<set>|<expr>/<set> <set>::= (<E>)|i Для предложения i+i*i существует единственное синтаксическое дерево:
В данном случае, операндами для +, согласно дереву, являются <E>. из которого получается I, и <expr>, из которого в свою очередь получается i*i. Это означает, что умножение должно быть выполнено первым для того, чтобы образовать <expr> для сложения, следовательно, умножение предшествует сложению. В результате, исходная грамматика оказалось одназначной.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|



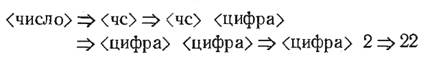
 В таком случае исходная грамматика является неоднозначной.
В таком случае исходная грамматика является неоднозначной.