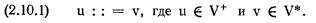Грамматика и язык. Классификация Хомского.

ПРОЕКТИРОВАНИЕ ТРАНСЛЯТОРОВ

Логические части трансляторов и этапы трансляции.

Транслятор - это программа, которая переводит исходную программу в эквивалентную ей

объектную программу. Объектная программа – программа на машинном языке. Процессперевода называется трансляцией.

Интерпретатор для некоторого исходного языка принимает исходную программу, написанную на этом языке, как входную информацию и исполняет ее.

Компилятор - это программа, предназначенная для перевода программы, написанной на каком-либо языке, в программу в машинных кодах. Процесс такого перевода называется компиляцией.

Различие между компилятором и интерпретатором в том, что интерпретатор не порождает объектную программу.

Логические части компилятора:

Пунктирные стрелки обозначают информационные потоки, тогда как сплошные указывают порядок работы подпрограмм.

Таблица символов – список

идентификаторов, встречающихся в исходной программе, вместе с их атрибутами (тип, значение и любая другая информация, которая может понадобиться при генерации объектной программы).

Таблица констант содержит константы, используемые в исходной программе.

Таблица циклаотображает структуру вложений циклов и хранит данные о переменных цикла.

Невозможно точно определить вид и содержание информации, которую следует собирать, до тех пор, пока не будут продуманы команды объектной программы для каждой инструкции исходной и сама синтезирующая часть компилятора. Многое зависит от глубины задуманной оптимизации.

Сканер – самая простая часть, также называемая лексическим анализатором. Просматривает литеры исходной программы слева направо и строит символы программы – идентификаторы, операторы, целые числа и прочие. Символы иногда называют элемент или атом. На этой стадии можно исключить комментарий, занести идентификаторы в таблицу символов и выполнить другую работу, которая не требует анализа исходной программы.

Синтаксический и семантический анализаторы выполняют сложную работу по расчленению программы на составные части, формированию ее внутреннего представления и заполнения таблиц. Когда синтаксический анализатор узнает конструкцию исходного языка, он вызывает соответствующую семантическую процедуру, которая контролирует конструкцию с точки зрения семантики и затем запоминает информацию о ней в таблицах. Например, встретив последовательность символов “x = 10”, семантический анализатор проверит соответствие типов и лишь затем сделает запись в таблице.

Внутреннее представление исходной программы в значительной степени зависит от его дальнейшего использования. Это может быть дерево, отражающее синтаксис исходной программы. Это может быть исходная программа в обратной польской записи (форма записи выражений, в которой операнды расположены перед знаками операций).

Еще одна форма – список тетрад – оператор, операнд, операнд, результат.

При подготовке к генерации команднадо распределить память под переменные готовой программы и попытаться оптимизировать программу (пока ее внутреннее представление).

На этапе генерации команд происходит перевод внутреннего представления в машинный код. Наиболее кропотливая, но наиболее понятная часть.

Часто бывает нужно пройти по исходному коду несколько раз, в связи с этим различают однопроходные и многопроходные компиляторы.

Формы записи грамматик и внутреннего представления кода.

Основная форма записи – форма Бекуса-Наура.

Форма Бэкуса—Наура (сокр. БНФ) — формальная система описания синтаксиса, в которой одни синтаксические категории последовательно определяются через другие категории. БНФ используется для описания контекстно-свободных формальных грамматик. Используется для описания синтаксиса языков программирования, данных, протоколов и т. д.

БНФ-конструкция определяет конечное число символов (нетерминалов). Кроме того, она определяет правила замены символа на какую-то последовательность букв (терминалов) и символов. Процесс получения цепочки букв, можно определить поэтапно: изначально имеется один символ (символы обычно заключаются в угловые скобки, а их название не несёт никакой информации). Затем этот символ заменяется на некоторую последовательность букв и символов, согласно одному из правил. Затем процесс повторяется (на каждом шаге один из символов заменяется на последовательность, согласно правилу). В конце концов, получается цепочка, состоящая из букв (и не содержащая символов). Это означает, что полученная цепочка может быть выведена из начального символа.

БНФ-конструкция состоит из нескольких предложений вида

<определяемый символ> ::= <посл.1> | <посл.2> | . . . | <посл.n>

описывающих правила. Такое правило, означает, что символ <определяемый символ> может заменяться на одну из последовательностей посл.1. Знак определения, обычно выглядит как ::=, но возможны и другие варианты.

Внутреннее представление:

· дерево

· обратная польская запись

· список тетрад

Грамматика и язык. Классификация Хомского.

Правилом называется упорядоченная пара (U, х), которая обычно записыва­ется так:

U : :=х,

где U — символ, а х — непустая конечная цепочка символов.

U называется левой частью, а х — правой частью правила.

Грамматикой G [Z] называется ко­нечное, непустое множество правил; Z — это символ, который дол­жен встретиться в левой части по крайней мере одного правила. Он называется начальным символом . Все символы, которые встре­чаются в левых и правых частях правил, образуют словарь V. Символы, которые встречаются в левой части, называются нетерминалами, символы которые не входят в это множество образуют множество терминалов.

Сентенциальной формой называется цепочка х, если она выводима из начального символа грамматики z =>* x

Цепочка– это всякая конечная последовательность алфавита.

Алфавит– непустое конечное множество элементов, называемых символами.

Непосредственный вывод: vнепосредственно порождаетw(v=>w), если для цепочек x, yможно записатьv::=xUy, w ::= xuyи U::=u.Тогда w непосредственно выводимо из v.

Вывод: vпорождает w(v=>+w), еслисуществует последовательность непосредственных выводовv::=v0=>…vn::=w, гдеn>1(v=>*w –количество выводов может быть равно 0).

Начальный символ грамматики – символ из которого выводимы все правила грамматики.

Классификация по Хомскому:

Хомский определил четыре основных класса языков в тер­минах грамматик, являющихся упорядоченной четверкой (V, Т, Р, Z), где

Язык, порождаемый грамматикой, — это множество терминаль­ных цепочек, которые можно вывести из Z. Различие четырех типов грамматик заключается в форме правил подстановки, допустимых в Р. Говорят, что G — это (по Хомскому) грамматика типа 0 или грамматика с фразовой структурой, если правила имеют вид

То есть левая часть и может быть тоже последовательностью сим­волов, а правая часть может быть пустой. Грамматикам с фразовой структурой посвящено сравнительно немного работ. Если ввести ограничение на правила подстановки, то получится более интерес­ный класс языков типа 1, называемых также контекстно-чувст­вительными или контекстно-зависимыми языками. В этом слу­чае правила подстановки имеют следующий вид:

Термин «контекстно-чувствительная» отражает тот факт, что можно заменить U на и лишь в контексте х . . . у. Дальнейшее огра­ничение дает класс грамматик, полностью подобный классу, кото­рый мы используем; грамматика называется контекстно-свободной (тип 2), если все ее правила имеют вид

Этот класс назван контекстно-свободным потому, что символ U можно заменить цепочкой и, не обращая внимания на контекст, в котором он встретился. В КС-грамматике может появиться пра­вило вида U : = Λ, где Λ — пустая цепочка. Однако, чтобы не усложнять терминологию и доказательства, мы не допускаем таких правил в наших грамматиках. По заданной КС-грамматике G мож­но сконструировать Λ-свободную (или неукор ачивающую) грам­матику G1 (наш тип),- такую, что L (Gl) = L (G) — {Λ}. Более того, если G однозначна, то G1 также однозначна, поэтому факти­чески мы не вносим ограничений.

Если мы ограничим правила еще раз, приведя их к виду

то получим грамматику типа 3, или регулярную грамматик). Регулярные грамматики играют основную роль как в теории язы­ков, так и в теории автоматов. Множество цепочек, порождаемых регулярной грамматикой, «допускается» машиной, называемой ав­томатом с конечным числом состояний (которую мы определим в следующей главе), и наоборот. Таким образом, мы имеем характе­ристику этого класса грамматик в терминах автомата. Регулярные языки (те, что порождаются регулярными грамматиками), кроме того, называются регулярными множествами. Известно, что если

Вводя все большие ограничения, мы определили четыре класса грамматик. Таким образом, есть языки с фразовой структурой, ко­торые не являются контекстно-чувствительными, контекстно-чувствительные языки, которые не являются контекстно-свобод­ными, и контекстно-свободные, которые не являются регулярными.

Не нашли, что искали? Воспользуйтесь поиском по сайту: