|
|
Метод потенциалов. 2 версия ответа.12
Согласно теореме о потенциалах, каждой занятой клетке будет соответствовать уравнение Для исследования плана на оптимальность по каждой свободной клетке прове-ряется условие
Если для всех свободных клеток оценки В общем случае цикл представляет собой замкнутую ломаную линию, состоящую из звеньев, пересекающихся под прямым углом. Каждое звено соединяет две клетки строки (столбца). Цикл включает одну свободную клетку, остальные клетки цикла заняты. В цикле всегда четное число клеток. Для свободной клетки всегда можно построить единственный цикл. Если из занятых клеток образуется цикл, то план перевозок не является опорным. Цикл строится лишь для свободных клеток.
Сформулируем алгоритм решения ТЗ методом потенциалов: 1) построить опорный план; 2) вычислить потенциалы поставщиков и потребителей 3) вычислить оценки Пример 17.1. В пунктах
Требуется: 1) методом потенциалов найти план перевозок продукции, при котором минимизируются суммарные затраты по ее изготовлению и доставке потребителям; 2) вычислить суммарные затраты fmin.
Решение. 1) Найдем суммарные запасы продукции и суммарные потребности Данные задачи заносим в таблицу 1. Табл. 1.
Начальный опорный план получим по правилу «минимального элемента». Загрузку начинаем с клетки, которой соответствует наименьший тариф cij≠0 всей матрицы тарифов. В нашем случае минимальным тарифом является с14=1, который соот-ветствует клетке (1, 4). В эту клетку вписываем x14=min (360; 200)=200. Исключаем четвертый столбец. У поставщика A1 осталось еще 160 единиц продукции, которые по-местим в клетку (1, 2). Исключаем первую строку. Но потребителю B2 необходимо еще 30 ед. продукции, которые берем у поставщика A2, и помещаем в клетку (2, 3). Исключаем второй столбец. Оставшиеся у поставщика A2 120 ед. продукции помещаем в клетку (2, 3). Исключаем вторую строку. Необходимые потребителю B3 220 ед. продукции берем у поставщика A3 и помещаем в клетку (3, 3). Исключаем третий столбец. В пункте A3 оставшиеся 160 ед. продукции помещаем в клетку (3; 1). Исключаем третий столбец. Оставшиеся 110 ед. помещаем в клетку (4; 1). Полученный нами план является невырожденным, так как выполняется условие базисных клеток: m+n-1=4+4-1=7, и число заполненных клеток тоже 7. А значит, полу-чено опорное решение, которое запишем матрицей
Методом потенциалов проверим, является ли полученное решение оптимальным. Для этого каждому поставщику и потребителю придается число, называемое потен-циалом. Потенциалы выбираем так, чтобы их сумма для каждой загруженной клетки была равна тарифу перевозки единицы груза, т.е. ui+vj=cij, где ui – потенциал i-го поставщика; vj – потенциал j-го потребителя; cij – тариф заполненной клетки. В нашем случае получаем следующие уравнения:
Полагая v4=0, получаем следующие потенциалы: u1=1 u3=3 v1= 0 v3= 4 u2=0 u4=0 v2= 2 v4=0
Все полученные данные заносим в таблицу 2.
Далее вычисляем оценки свободных клеток по формуле: s11=c11-(u1+v1) =7-(1+0) =6 ³ 0 s24=c24-(u2+v4) = 8-(0+0) =8 ³ 0 s42=c42-(u4+v2) = 0-(0+2) = -2 s13=c13-(u1+v3) = 6-(1+4) =1 ³ 0 s32=c32-(u3+v2) = 5-(3+2) = 0 s43=c43-(u4+v3) = 0-(0+4) = -4 s21=c21-(u2+v1) = 5-(0+0) =5 ³ 0 s34=c34-(u3+v4) = 9-(3+0) = 6 ³ 0 s44=c44-(u4+v4) = 0-(0+0) = 0 Так как s42<0, и s43<0 то полученный план не является оптимальным. Наиболее потенциальной клеткой является клетка (4; 3). Поэтому строим для клетки (4; 3) замк-нутый цикл, который в таблице 2 выделяем пунктирной линией: (4, 3)→(3, 3)→(3, 1)→(4, 1). Свободной клетке условно приписываем знак «+», тогда следующей клетке по ходу часовой стрелки – знак «-» и т.д., знаки чередуются. В отрицательных вершинах цикла определяем наименьшую загрузку клетки, т.е. min (x33, x41)=min (220, 110)=110. Количество продукции, равное 110ед., прибавляем к поставкам в клетках со знаком «+» и вычитаем из поставок в клетках со знаком «-». Получаем новый план, который заносим в таблицу 3.
Проверяем, является ли полученный план оптимальным. Для этого каждому поставщику и потребителю придаем число – потенциал. Вычисляем потенциалы так же, как это делали выше:
Полагая v3=0, получаем следующие потенциалы, которые заносим в таблицу 4: u1=5 u3=7 v1= -4 v3= 0 u2=4 u4=0 v2= -2 v4= -4 Вычисляем оценки свободных клеток: s11=7-(5-4) =6 ³ 0 s24=8-(4-4) = 8 ³ 0 s41=0-(0-4) = 4 ³ 0 s13=6-(5+0) =1 ³ 0 s32=5-(7-2) = 0 s42=0-(0-2) =2 ³ 0 s21=5-(4-4) =5 ³ 0 s34=9-(7-4) = 6 ³ 0 s44=0-(0-4) = 4 ³ 0
Поскольку все sij>0, то полученный план является оптимальным, который можно представить в виде матрицы
2) Суммарные затраты fmin при этом будут составлять:
Ответ:
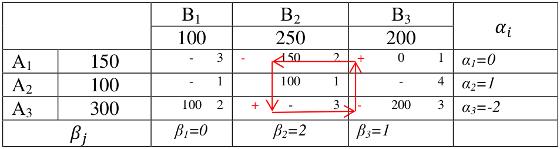
Вопрос 25. Понятия контуpа пеpесчета (цикла) . Пpизнак оптимальности плана. После того, как получено допустимое решение, его надо проверить на оптимальность с помощью метода потенциалов. Перед проверкой убеждаемся, что число заполненных клеток равно соотношению m+n-1. В нашей таблице их 3+3-1=5. Признак оптимальности: решение оптимально, если во всех свободных клетках выполняется неравенство: αi + cij ≥ βj, где αi и βj – потенциалы, cij – тарифы перевозок. Вычислим αi и βj с помощью выше указанного неравенства:
Принято считать, что α1 всегда равно 0. Если не сделать это допущение, то задача не будет иметь решение. Вычисления остальных значений потенциалов производят по базовым (заполненным) клеткам: Проверку на оптимальность делают по свободным клеткам с помощью этого же неравенства: В результате проверки мы выявили три недостаточные клетки. Находим цикл пересчета: цикл пересчета – это ход ладьи по базовым клеткам с чередованием знаков «+» и «-», начиная с недостаточной клетки и замыкаясь в ней же.
В клетках с минусовыми отметками выбирает минимальное число. В нашем случае это число равно 100. Пересчет делают следующим образом: где стоит знак «-» это число отнимают, а где «+» то прибавляют. Значения, не входящие в цикл пересчета переписывают без изменений. Получает таблицу, в которой соотношение m+n-1 не выполняется, и поэтому выбираем клетку с минимальным тарифом и, проставляя в ней ноль, считаем ее условно базовой:
Вначале транспортные расходы составляли 1400 у.е. Считаем сейчас: Полученное решение снова проверяем на оптимальность:
Проверка выявляет одну недостаточную клетку, для которой находим цикл пересчета: В отрицательных клетках из двух значений выбираем число 150, которое отнимаем, где знак «-» и прибавляем где знак «+»:
Транспортные расходы: Проверяем снова на оптимальность и убеждаемся, что найден оптимальный план: Ответ: f = 1050 у.е. Вторая версия Ответа 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Так как всех занятых клеток должно быть
. Так как всех занятых клеток должно быть 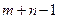 , т.е. на единицу меньше, то для определения чисел
, т.е. на единицу меньше, то для определения чисел  и
и  , необходимо решить систему из
, необходимо решить систему из  неизвестными. Система неопределенная, и, чтобы найти част-ные решения, одному из потенциалов придается произвольной числовое значение, тогда остальные потенциалы определятся однозначно. Для облегчения расчетов одному из по-тенциалов придается обычно значение, равное нулю.
неизвестными. Система неопределенная, и, чтобы найти част-ные решения, одному из потенциалов придается произвольной числовое значение, тогда остальные потенциалы определятся однозначно. Для облегчения расчетов одному из по-тенциалов придается обычно значение, равное нулю. . Если хотя бы одна свободная не удовлетворяет данному усло-вию, то опорный план не является оптимальным, его можно улучшить за счет загрузки этой клетки. Если таких клеток несколько, то наиболее перспективной для загрузки является клетка, для которой разность (оценка) между тарифом клетки и суммой потенциалов наименьшая, т.е.
. Если хотя бы одна свободная не удовлетворяет данному усло-вию, то опорный план не является оптимальным, его можно улучшить за счет загрузки этой клетки. Если таких клеток несколько, то наиболее перспективной для загрузки является клетка, для которой разность (оценка) между тарифом клетки и суммой потенциалов наименьшая, т.е. .
. , то опорный план перевозок явля-ется оптимальным. Если для опорного плана перевозок указанное условие оптимальности не выполняется, то за счет загрузки свободной клетки с отрицательной оценкой план перевозки улучшается. Для наиболее перспективной свободной клетки строится замк-нутый цикл с вершинами в загруженных клетках. Вершинам этого цикла условно припи-сываются знаки: свободной клетке – знак «+», следующей по часовой или против часовой стрелки занятой клетке – знак «-», следующей – снова «+» и т.д. Из поставок в клетках цикла с «отрицательными» вершинами выбирается наименьшее количество l груза, ко-торое и перемещается по клеткам этого цикла: прибавляется к поставкам в положи-тельных вершинах и вычитается из поставок в отрицательных вершинах, в результате чего баланс цикла не нарушается.
, то опорный план перевозок явля-ется оптимальным. Если для опорного плана перевозок указанное условие оптимальности не выполняется, то за счет загрузки свободной клетки с отрицательной оценкой план перевозки улучшается. Для наиболее перспективной свободной клетки строится замк-нутый цикл с вершинами в загруженных клетках. Вершинам этого цикла условно припи-сываются знаки: свободной клетке – знак «+», следующей по часовой или против часовой стрелки занятой клетке – знак «-», следующей – снова «+» и т.д. Из поставок в клетках цикла с «отрицательными» вершинами выбирается наименьшее количество l груза, ко-торое и перемещается по клеткам этого цикла: прибавляется к поставкам в положи-тельных вершинах и вычитается из поставок в отрицательных вершинах, в результате чего баланс цикла не нарушается. и
и  , решив систему уравнений вида
, решив систему уравнений вида  для всех свободных клеток по формуле
для всех свободных клеток по формуле  . Если
. Если  , то по-лученный оптимальный план единственный. В случае, если хотя бы одна оценка
, то по-лученный оптимальный план единственный. В случае, если хотя бы одна оценка  , имеем бесчисленное множество оптимальных планов с одним и тем же значением целевой функции.
, имеем бесчисленное множество оптимальных планов с одним и тем же значением целевой функции. производится однородная продукция в коли-чествах
производится однородная продукция в коли-чествах  единиц. Готовая продукция поставляется в пункты
единиц. Готовая продукция поставляется в пункты  , потребности которых составляют
, потребности которых составляют  единиц. Стоимость cij перевозки единицы продукции из пункта Ai в пункт Bj заданы матрицей
единиц. Стоимость cij перевозки единицы продукции из пункта Ai в пункт Bj заданы матрицей  :
: .
. 150+380=890; b1+b2+b3+b4=270+190+340+200=1000. Поскольку
150+380=890; b1+b2+b3+b4=270+190+340+200=1000. Поскольку  ,то есть отсутствует баланс между производимой продукцией и потребнос-тями, то мы имеем задачу открытого типа. Вводим фиктивного поставщика A4, который имеет запас продукции в объеме
,то есть отсутствует баланс между производимой продукцией и потребнос-тями, то мы имеем задачу открытого типа. Вводим фиктивного поставщика A4, который имеет запас продукции в объеме  (един.). Все тарифы на доставку продукции фиктивного поставщика равны нулю, т.е. c41=c42=c43=c44=0
(един.). Все тарифы на доставку продукции фиктивного поставщика равны нулю, т.е. c41=c42=c43=c44=0 .
.

 .
.
 .
. .
. Потребитель B3 не дополучил 110 единиц продукции.
Потребитель B3 не дополучил 110 единиц продукции.