
|
|
По критерию стоимости в матричной форме.12 Транспортная задача.
Вопрос 21, 22. Постановка транспортной задачи по критерию стоимости в матричной форме.
Рассмотрим простейший вариант модели транспортной задачи (ТЗ), когда речь идет о рациональной перевозке некоторого однородного продукта от производителя к потребителям; при этом имеется баланс между суммарным спросом потребителей и возможностями поставщиков по их удовлетворению. Причем потребителям безразлично, из каких пунктов производства будет поступать продукция, лишь бы их заявки были полностью удовлетворены. Так как от схемы прикрепления потребителей к поставщикам существенно зависит объем транспортной работы, возникает задача о наиболее рацио-нальном прикреплении, правильном направлении перевозок грузов, при котором потреб-ности полностью удовлетворяются, вся продукция от поставщиков вывозиться, а затраты на транспортировку минимальны. Транспортную задачу можно сформулировать следующим образом, представив ее в виде таблицы, которую называют распределительной. Распределительную таблицу назы-вают иногда табличнойили матричной моделью ТЗ.
В m пунктах отправления A1, …, Am сосредоточен однородный груз в количествах соответственно a1, …, am единиц. Имеющийся груз необходимо доставить потребителям B1, …, Bn, спрос которых выражается величинами b1, …, bn единиц. Известна стоимость cij перевозки единицы груза из i-го Для составления математической модели задачи введем переменные xij
Цель транспортной задачи – минимизировать общие затраты на реализацию плана перевозок, которые можно представить целевой функцией:
Переменные должны удовлетворять следующим условиям: 1) ограничения по запасам:
2) ограничения по потребностям:
3) условия неотрицательности: xij ³0 где cij – стоимость перевозки единицы груза из i-го
Если план перевозок Теорема 17.1. (о существовании допустимого плана). Для того чтобы ТЗ имела допустимые планы, необходимо и достаточно выпол-нение равенства
Модель ТЗ называется закрытой, если суммарный объем груза, имеющегося у поставщиков, равен суммарному спросу потребителей, т.е. выполняется равенство
Если для ТЗ выполняется одно из условий:
то модель задачи называется открытой. Для разрешимости ТЗ с открытой моделью необходимо преобразовать ее в закры-тую. Так, при выполнении условия Аналогично при выполнении условия При преобразовании открытой задачи в закрытую целевая функция не меняется, так как все слагаемые, соответствующие дополнительным перевозкам, равны нулю.
Вопрос 23. Построение исходного опорного плана.
Построение опорных планов, а также преобразование их проводят непосредственно в распределительной таблице. Если в плане перевозок переменная Для построения начального опорного плана в распределительной таблице исполь-зуют такие правила и методы, как правило «северно-западного угла», правило «мини-мального элемента», метод Фогеля. Существует несколько методов составления исходного опорного плана. Самый простой из них – метод «северо-западного угла». Исходные данные примера (затраты на перевозку единицы продукции от каждого поставщики к каждому потребителю) приведены в верхних правых углах таблицы 2.5.1. Таблица 2.5.1
Метод наименьшего элемента состоит в заполнении клеток, начиная с тех, в которых стоят наименьшие затраты на перевозку (см. табл. 2.5.1). В данном случае минимальную стоимость имеют перевозки по каналу А4-В2 – 8 у.д.е. Ставим в эту клетку максимально возможное количество перевозок – 175 (т.к. возможности А4=175). Следующие по затратам на перевозку каналы А4-В5 и А4-В4. Однако, возможности А4 уже исчерпаны, поэтому далее заполняется клетка, соответствующая каналу А2-В4, в которую ставим 152 единицы груза (А2=152). Далее заполняем клетку А2-В2. Сюда можно поставить только 25, т.к. второму потребителю требуется 200, а 175 он уже получает от А4. Следующие по затратам перевозки по каналу А2-В4 – 11 у.д.е. В эту клетку можно поставить только 127 единиц продукции, т.к. А2=152, а он уже поставил 25 единиц потребителю В2. Канал А2-В5 и А3-В2 не рассматриваем, т.к. возможности А2 уже исчерпаны, а потребности В2 полностью удовлетворены. Поэтому затем заполняется клетка, соответствующая каналу А3-В3(затраты на перевозку – 42 у.д.е.) В дальнейшем транспортная таблица заполняется аналогично. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 пункта отправления в j-й
пункта отправления в j-й  пункт назначения. Удельные транспортные издержки (расходы) записывают в форме матрицы
пункт назначения. Удельные транспортные издержки (расходы) записывают в форме матрицы  , которую называют матрицей тарифов. Требуется спланировать перевозки, т.е. указать, сколько единиц груза должно быть отправлено от i-го поставщика j-му потребителю, так, чтобы максимально удовлетворить спрос потребителей и чтобы суммарные транспортные затраты на перевозки были при этом минимальными. Рассмотрим простейший случай, когда суммарные запасы поставщиков равны суммарным потребностям
, которую называют матрицей тарифов. Требуется спланировать перевозки, т.е. указать, сколько единиц груза должно быть отправлено от i-го поставщика j-му потребителю, так, чтобы максимально удовлетворить спрос потребителей и чтобы суммарные транспортные затраты на перевозки были при этом минимальными. Рассмотрим простейший случай, когда суммарные запасы поставщиков равны суммарным потребностям 
 , обозначающие количество единиц груза, которые необходимо доставить из i-го пункта отправления в j-й пункт назначения. Все эти переменные можно записать в виде матрицы
, обозначающие количество единиц груза, которые необходимо доставить из i-го пункта отправления в j-й пункт назначения. Все эти переменные можно записать в виде матрицы  , которая будет называться матрицей перевозок:
, которая будет называться матрицей перевозок: .
. . (17.1.1.)
. (17.1.1.) (17.1.2.)
(17.1.2.) (17.1.3.)
(17.1.3.) - количество груза, сосредоточенного в пункте
- количество груза, сосредоточенного в пункте  ;
; - количество груза, необходимое для доставки потребителю
- количество груза, необходимое для доставки потребителю  .
. (17.1.5.)
(17.1.5.) или
или  ,
, -й пункт назначения
-й пункт назначения  , т.е. в матрице задачи предусматривается дополнительный столбец. Спрос фиктивного потребителя полагают равным небалансу, т.е.
, т.е. в матрице задачи предусматривается дополнительный столбец. Спрос фиктивного потребителя полагают равным небалансу, т.е. 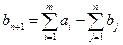 , а все тарифы – одинаковыми, чаще всего равными нулю
, а все тарифы – одинаковыми, чаще всего равными нулю  .
. , у которого запас груза равен
, у которого запас груза равен  , а тарифы дополнительной строки распределительной таблицы равны нулю, т.е.
, а тарифы дополнительной строки распределительной таблицы равны нулю, т.е.  .
. равна некоторому числу
равна некоторому числу 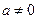 , то это число записывают в соответствующую клетку
, то это число записывают в соответствующую клетку  и считают ее занятой (или базисной), если же
и считают ее занятой (или базисной), если же  , то клетку
, то клетку 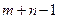 , а остальные
, а остальные 
 клеток будут свободными.
клеток будут свободными.