
|
|
Универсальный закон электромагнитной индукцииИзменение магнитного потока, пронизывающего контур, может возникнуть не только в результате его движения в магнитном поле, но и при изменении величины индукции магнитного поля, пронизывающего контур. Закономерен вопрос: какова природа сторонних сил в этом случае? Свободные электроны в проводнике находятся в хаотическом движении, на каждый электрон действует магнитная сила Лоренца, но так как движение электронов хаотическое, то сумма всех магнитных сил Лоренца, действующих на отдельные электроны, равна нулю. Поэтому магнитная сила Лоренца не может играть роль сторонней силы в случае, когда проводник неподвижен. Заставить двигаться заряды в неподвижном проводнике может только сила Кулона. Анализируя явление электромагнитной индукции, Максвелл пришел к выводу, что причина появления электродвижущей силы индукции заключается в возникновении электрического поля при изменении магнитного потока через поверхность, ограниченную контуром. Следовательно, и индукционный ток также возникает под действием электрического поля, создающегося за счет изменения магнитного поля. Как всякое электрическое поле, оно совершает работу по перемещению заряда в цепи. Однако здесь имеются и свои принципиальные особенности. Существенной особенностью этого поля является то, что оно не является электростатическим. Силовые линии электростатического поля всегда разомкнуты, они начинаются и заканчиваются на электрических зарядах или в бесконечности, и в соответствии с этим работа этих сил на замкнутом контуре равна нулю. Поэтому электростатическое поле не может поддерживать движение зарядов по замкнутому контуру и, следовательно, не может привести к возникновению электродвижущей силы. Электрическое поле, возникающее в процессе изменения магнитного поля, не связано с каким-либо распределением электрических зарядов. Силовые линии электрического поля, связанного с переменным магнитным полем, не имеют начала и конца – они замкнуты наподобие силовых линий магнитного поля. Такое поле называется вихревым. Вихревое электрическое поле, возникающее в процессе электромагнитной индукции, создает электрический ток в замкнутом проводнике, следовательно, оно способно вызывать движение электронов по замкнутым траекториям, при этом сторонними силами являются силы вихревого электрического поля. Работа сил этого поля на замкнутой траектории не равна нулю. Именно этой работой определяется электродвижущая сила индукции в замкнутом контуре. Следует подчеркнуть, что вихревое электрическое поле при изменении магнитного потока существует независимо от того, есть ли в этом месте замкнутый контур. Контур является лишь индикатором, с помощью которого можно обнаружить наличие вихревого электрического поля. Таким образом, одним из основных положений электромагнитной теории Максвелла является утверждение, согласно которому всякое изменение магнитного поля вызывает появление вихревого электрического поля. Переменное магнитное поле неразрывно связано с этим электрическим полем, и поэтому говорят, что в этом случае мы имеем дело с электромагнитным полем Явление самоиндукции Важным частным случаем явления электромагнитной индукции называют явление самоиндукции. В этом случае изменяющийся магнитный поток через замкнутый контур создается переменным током в самом контуре. Рассмотрим тонкий замкнутый проводник, по которому течет ток силой
Коэффициент пропорциональности За единицу индуктивности в системе единиц СИ принимается индуктивность такого проводника, у которого при силе тока в нем в 1 А возникает сцепленный с ним поток, равный 1 Вб. Эту единицу называют генри (Гн):
Для примера вычислим индуктивность идеального соленоида, пренебрегая при этом краевыми эффектами. Пусть
Если ток в проводнике меняется, то меняется и магнитный поток, пронизывающий контур, вследствие чего в витке индуцируется электродвижущая сила самоиндукции
Знак минус в этой формуле обусловлен правилом Ленца. В рассматриваемом случае причиной, вызывающей электродвижущую силу самоиндукции, является изменение тока в цепи. Если ток в цепи возрастает, то возрастает и индукция магнитного поля, которое он создает, а следовательно, возрастает магнитный поток через контур. Поэтому, согласно правилу Ленца, ток самоиндукции должен быть направлен так, чтобы его магнитное поле препятствовало такому изменению магнитного потока, то есть навстречу основному току. И наоборот, при уменьшении силы тока в цепи направление индукционного тока будет совпадать с направлением основного тока.
Явление самоиндукции можно сопоставить с явлением инерции в механике. Инерция приводит к постепенному уменьшению скорости движения тел, даже при мгновенном приложении силы. Самоиндукция препятствует мгновенному изменению тока в электрической цепи. Поэтому индуктивность катушки L в электрической цепи играет ту же роль, что и масса m, являющаяся мерой инерции в механике.
Явление самоиндукции можно наблюдать на опыте, схема которого представлена на рис. 6.4. При замыкании цепи лампочка Электродвижущая сила самоиндукции, возникающая при выключении тока, может быть велика и поэтому опасна. Индуктивность большого электромагнита, применяемого для исследований, может составлять, например, 10 Гн. Ток в катушке может достигать 100 А. Если ток в цепи прервать с помощью выключателя или если будет случайный разрыв в цепи, то возникнет электродвижущая сила, равная Энергия магнитного поля
Магнитное поле обладает энергией. Чтобы убедиться в этом, рассмотрим электрическую цепь, содержащую соленоид, имеющий индуктивность При уменьшении тока в цепи уменьшается и индукция магнитного поля. Поэтому можно, по-видимому, говорить об энергии электрического тока или энергии магнитного поля, создаваемого током. В случае постоянных токов нельзя однозначно определить, где локализована эта энергия. Ответ на этот вопрос можно дать, изучая переменные магнитные поля или электромагнитные волны. В электромагнитных волнах переменные магнитные поля могут существовать без токов, их поддерживающих. Так как электромагнитные волны переносят энергию, можно заключить, что энергия сосредоточена в магнитном поле. Найдем величину энергии магнитного поля. Из закона сохранения энергии следует, что, когда ток прекратится, магнитное поле исчезнет, и вся энергия магнитного поля перейдет в тепловую энергию. Согласно закону Джоуля–Ленца, за малое время
С учетом этого равенства выделившееся количество теплоты можно записать в виде:
в этом выражении
Сравните выражение для магнитной энергии, запасенной в катушке индуктивности, с выражением для энергии электрического поля, запасенной в конденсаторе:
Энергия электрического поля в конденсаторе пропорциональна квадрату заряда, энергия магнитного поля, запасенная в катушке индуктивности, пропорциональна квадрату силы тока, то есть зависит от скорости движения зарядов. Напомним, что магнитное поле создается движущимися зарядами. Работа индукционного тока сопровождается нагреванием проводником за счет энергии магнитного поля, которое не может исчезнуть бесследно. Соленоид, таким образом, служит своеобразным резервуаром энергии, значение которой вычисляется по формуле
Энергию магнитного поля можно выразить через величины, характеризующие само поле. Сделаем это для магнитного поля, создаваемого током в длинном соленоиде. В этом случае
Так как магнитное поле внутри соленоида является однородным, то плотность энергии магнитного поля, запасенной в соленоиде, равна энергии, деленной на объем соленоида:
Пример Определим энергию магнитного поля соленоида. Обычный лабораторный соленоид длиной 10 см, площадью поперечного сечения 75 см2 и числом витков, намотанных в несколько слоев, равным 3 400, обладает индуктивностью
Это уже немалая энергия! Если, без специальных мер предосторожности, быстро разомкнуть цепь электромагнита, то при Взаимная индукция
Рассмотрим два неподвижных контура 1 и 2, расположенных достаточно близко друг к другу (рис. 6.8). Будем полагать, что среда является неферромагнитной. Если в контуре 1 течет ток силой, то он создает через контур 2 магнитный поток, пропорциональный
Аналогично, если в контуре 2 течет ток силой
Коэффициенты пропорциональности Можно показать, что при отсутствии ферромагнетиков коэффициенты Если контуры неподвижны и ферромагнетиков вблизи них нет, то при изменении силы тока в одном из контуров в другом контуре возникает электродвижущая сила индукции. Это явление называется явлением взаимной индукции. Согласно закону электромагнитной индукции электродвижущие силы индукции, возникающие в контурах 1 и 2, равны соответственно
Если в каком-либо контуре, например, в контуре 1 есть внешний источник электродвижущей силы
где
Аналогичное соотношение можно записать и для определения силы тока во втором контуре. В отличие от индуктивности, которая всегда положительная, взаимная индуктивность величина алгебраическая (в частности, равная нулю). Из рис. 6.8 видно, что знак магнитного потока Другими словами, Пример
При отсутствии устойчивого сигнала сотовой связи телефон становится более чувствительным к электромагнитным помехам. Происходит это из-за изменения сигнала вследствие явления взаимоиндукции. Пример такого эффекта – ухудшение приема телефона при приближении к телевизору или радиоприемнику. 6.6. Примеры на применение явления 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Этот ток создает пронизывающий контур магнитный поток. В соответствии с законом Био–Савара магнитная индукция пропорциональна силе тока, вызвавшего поле. Отсюда вытекает, что ток
. Этот ток создает пронизывающий контур магнитный поток. В соответствии с законом Био–Савара магнитная индукция пропорциональна силе тока, вызвавшего поле. Отсюда вытекает, что ток  .
. называется индуктивностью контура или коэффициентом самоиндукции. Линейная зависимость
называется индуктивностью контура или коэффициентом самоиндукции. Линейная зависимость  от
от  .
. – длина соленоида,
– длина соленоида,  – число витков на единицу длины,
– число витков на единицу длины,  – площадь одного витка. Индукция магнитного поля внутри соленоида равна
– площадь одного витка. Индукция магнитного поля внутри соленоида равна  . Тогда магнитный поток, пронизывающий соленоид, будет равен
. Тогда магнитный поток, пронизывающий соленоид, будет равен  , отсюда
, отсюда .
. . Если при этом индуктивность контура L остается неизменной, то электродвижущая сила самоиндукции, согласно основному закону электромагнитной индукции, имеет вид
. Если при этом индуктивность контура L остается неизменной, то электродвижущая сила самоиндукции, согласно основному закону электромагнитной индукции, имеет вид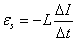 .
.


 , которая подключена к источнику тока через реостат R, вспыхивает мгновенно. Тогда как лампочка
, которая подключена к источнику тока через реостат R, вспыхивает мгновенно. Тогда как лампочка  , подключенная к источнику через катушку с большой индуктивностью, загорается с большим запозданием. Это объясняется тем, что в катушке в начальный момент возникает большая электродвижущая сила самоиндукции, которая в соответствии с правилом Ленца препятствует нарастанию тока в этой цепи. При размыкании цепи магнитный поток убывает, поэтому возникает ток самоиндукции, который препятствует уменьшению тока в катушке. Так как цепь уже разомкнута, индукционный ток будет течь через гальванометр (рис. 6.5), причем в направлении, противоположном первоначальному, что видно по отклонению стрелки гальванометра.
, подключенная к источнику через катушку с большой индуктивностью, загорается с большим запозданием. Это объясняется тем, что в катушке в начальный момент возникает большая электродвижущая сила самоиндукции, которая в соответствии с правилом Ленца препятствует нарастанию тока в этой цепи. При размыкании цепи магнитный поток убывает, поэтому возникает ток самоиндукции, который препятствует уменьшению тока в катушке. Так как цепь уже разомкнута, индукционный ток будет течь через гальванометр (рис. 6.5), причем в направлении, противоположном первоначальному, что видно по отклонению стрелки гальванометра. , даже если
, даже если  ,
, 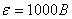 . В действительности это время гораздо меньше, и поэтому электродвижущая сила самоиндукции значительно больше. Возникающая при этом большая разность потенциалов, сосредоточенная на выключателе или разрыве, может привести к нагреву и плавлению контактов. Этим объясняется опасность резкого отключения от силовой сети мощных электродвигателей, обмотки которых обладают большой индуктивностью. Их отключают, плавно уменьшая ток с помощью реостатов.
. В действительности это время гораздо меньше, и поэтому электродвижущая сила самоиндукции значительно больше. Возникающая при этом большая разность потенциалов, сосредоточенная на выключателе или разрыве, может привести к нагреву и плавлению контактов. Этим объясняется опасность резкого отключения от силовой сети мощных электродвигателей, обмотки которых обладают большой индуктивностью. Их отключают, плавно уменьшая ток с помощью реостатов.
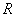 (рис. 6.6). При размыкании ключа К ток не сразу падает до нуля. В течение некоторого времени он продолжает течь, поддерживаемый возникающей в катушке электродвижущей силой самоиндукции, и при этом на сопротивлении выделяется тепло, согласно закону Джоуля–Ленца. Возникает вопрос, за счет каких запасов энергии выделяется тепло, ведь цепь разомкнута, и внешний источник отключен.
(рис. 6.6). При размыкании ключа К ток не сразу падает до нуля. В течение некоторого времени он продолжает течь, поддерживаемый возникающей в катушке электродвижущей силой самоиндукции, и при этом на сопротивлении выделяется тепло, согласно закону Джоуля–Ленца. Возникает вопрос, за счет каких запасов энергии выделяется тепло, ведь цепь разомкнута, и внешний источник отключен. на сопротивлении R выделится количество теплоты
на сопротивлении R выделится количество теплоты  . По закону Ома ток I равен
. По закону Ома ток I равен .
. ,
,
 так как ток убывает, а выделяющаяся теплота
так как ток убывает, а выделяющаяся теплота  . Зависимость магнитного потока от силы тока можно представить графически (рис. 6.7). Очевидно, что количество теплоты, выделившейся за время
. Зависимость магнитного потока от силы тока можно представить графически (рис. 6.7). Очевидно, что количество теплоты, выделившейся за время  , прямой
, прямой 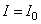 и осью
и осью  . Таким образом, энергия магнитного поля, создаваемого током I в катушке с индуктивностью L, равна
. Таким образом, энергия магнитного поля, создаваемого током I в катушке с индуктивностью L, равна .
.
 .
. .
.
 ,
,  , то есть
, то есть  . Подставив эти формулы в (6.4), получим
. Подставив эти формулы в (6.4), получим .
.
 .
.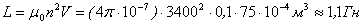 . Сопротивление такого соленоида 50 Ом. При использовании 6-вольтной батарейки установится ток
. Сопротивление такого соленоида 50 Ом. При использовании 6-вольтной батарейки установится ток  . Запасенная в соленоиде магнитная энергия равна
. Запасенная в соленоиде магнитная энергия равна  Это небольшая энергия. Однако эта энергия пропорциональна квадрату силы тока и может достигать больших значений. Так, например, в электромагнитах, используемых для исследований, магнитная индукция при максимальном токе составляет обычно от 1 до 1,5 Тл. Магнитная проницаемость железа
Это небольшая энергия. Однако эта энергия пропорциональна квадрату силы тока и может достигать больших значений. Так, например, в электромагнитах, используемых для исследований, магнитная индукция при максимальном токе составляет обычно от 1 до 1,5 Тл. Магнитная проницаемость железа  достигает значений в сотни и тысячи единиц, поэтому в электромагните большая часть энергии сосредоточена в зазоре между полюсами электромагнита. Если объем зазора составляет 0,2
достигает значений в сотни и тысячи единиц, поэтому в электромагните большая часть энергии сосредоточена в зазоре между полюсами электромагнита. Если объем зазора составляет 0,2  ,то запасенная энергия
,то запасенная энергия /
/  = 1,8
= 1,8  Дж.
Дж. мгновенная мощность составит Р = 1,8 МВт.
мгновенная мощность составит Р = 1,8 МВт.
 :
: .
.
 , он создает магнитный поток
, он создает магнитный поток  через контур 1:
через контур 1: .
.
 и
и  называют взаимной индуктивностью контуров. Из (6.6) и (6.7) видно, что взаимная индуктивность численно равна магнитному потоку через один из контуров при единичном токе в другом контуре. Коэффициенты
называют взаимной индуктивностью контуров. Из (6.6) и (6.7) видно, что взаимная индуктивность численно равна магнитному потоку через один из контуров при единичном токе в другом контуре. Коэффициенты 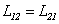 . Это свойство называется теоремой взаимности. Теорема взаимности позволяет не делать различия между
. Это свойство называется теоремой взаимности. Теорема взаимности позволяет не делать различия между 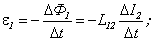
 .
. , то с учетом явления самоиндукции полную электродвижущую силу, действующую в этом контуре, можно записать следующим образом:
, то с учетом явления самоиндукции полную электродвижущую силу, действующую в этом контуре, можно записать следующим образом: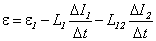 ,
,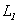 – индуктивность контура 1. Если сопротивление контура 1 равно
– индуктивность контура 1. Если сопротивление контура 1 равно  , то, согласно закону Ома, сила тока в этом контуре будет равна
, то, согласно закону Ома, сила тока в этом контуре будет равна .
. при данном направлении тока
при данном направлении тока  , если при положительных токах в обоих контурах они «подмагничивают» друг друга, в противном случае
, если при положительных токах в обоих контурах они «подмагничивают» друг друга, в противном случае  . В частных случаях можно заранее так установить положительные направления обхода контуров, чтобы получить желательный нам знак величины
. В частных случаях можно заранее так установить положительные направления обхода контуров, чтобы получить желательный нам знак величины 