
|
|
ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК2.1. Постоянный электрический ток. Электрическим током называется направленное движение электрических зарядов. Если в веществе содержатся свободные носители заряда – электроны, ионы, способные перемещаться на значительные расстояния, то при наличии электрического поля они приобретают направленное движение, которое накладывается на их тепловое хаотическое движение. В результате этого свободные носители заряда совершают дрейфовое движение в определенном направлении. Количественной характеристикой электрического тока служит величина заряда, переносимого через рассматриваемую поверхность в единицу времени. Ее называют силой тока. Если за время
Единица силы тока в системе единиц СИ – Ампер (A), В образовании тока могут участвовать как положительные, так и отрицательные носители; электрическое поле перемещает их в противоположных направлениях. Направление тока принято определять по направлению движения положительных носителей. На самом деле ток в большинстве случаев создается движением электронов, которые, будучи заряжены отрицательно, движутся в направлении, противоположном принятому за направление тока. Если в электрическом поле одновременно движутся положительные и отрицательные носители, то полный ток определяется как сумма токов, образованных носителями каждого знака. Для количественной характеристики электрического тока используется также другая величина, которая называется плотностью тока. Плотностью тока называется величина, равная заряду, проходящему за единицу времени через единичную площадку, перпендикулярную направлению движения зарядов. Плотность тока является векторной величиной.
Обозначим через n концентрацию носителей тока, то есть число их в единице объема. Проведем в проводнике с током бесконечно малую площадку DS, перпендикулярную к скорости заряженных частиц
Таким образом, через единицу площади за единицу времени переносится электрический заряд
где Поле вектора Электродвижущая сила Если в проводнике создать электрическое поле и не поддерживать это поле, то перемещение носителей тока приведет к тому, что поле внутри проводника исчезнет, и ток прекратится. Для того чтобы поддерживать ток в цепи достаточно долго, необходимо осуществить движение зарядов по замкнутой траектории, то есть сделать линии постоянного тока замкнутыми. Следовательно, в замкнутой цепи должны быть участки, на которых носители заряда будут двигаться против сил электростатического поля, то есть от точек с меньшим потенциалом к точкам с большим потенциалом. Это возможно лишь при наличии неэлектрических сил, называемых сторонними силами. Сторонними силами являются силы любой природы, кроме кулоновских. Физическая величина, равная работе сторонних сил при перемещении единичного заряда на данном участке цепи, называется электродвижущей силой (ЭДС), действующей на этом участке:
Электродвижущая сила – важнейшая энергетическая характеристика источника. Электродвижущая сила измеряется, как и потенциал, в вольтах. В любой реальной электрической цепи всегда можно выделить участок, который служит для поддержания тока (источник тока), а остальную часть рассматривать как «нагрузку». В источнике тока обязательно действуют сторонние силы, поэтому в общем случае он характеризуется электродвижущей силой Результирующая сила, действующая на заряд в каждой точке цепи, равна сумме сил электрических и сторонних:
Работа, совершаемая этой силой над зарядом
где Величина, численно равная работе Участок цепи, на котором не действуют сторонние силы, называется однородным. Участок, на котором на носители тока действуют сторонние силы, называется неоднородным. Для однородного участка цепи Закон Ома Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения на проводнике:
Под однородностью понимается отсутствие сторонних сил.Величина R называется электрическим сопротивлением проводника. Единицей сопротивления служит Ом, равный сопротивлению такого проводника, в котором при напряжении в
где
В изотропном проводнике упорядоченное движение носителей тока происходит в направлении вектора напряженности электрического поля
откуда
Воспользовавшись тем, что векторы
Величина Для участка цепи, на котором действуют сторонние силы, закон Ома запишется в следующей форме:
Перепишем (3.4) в виде
Эта формула выражает закон Ома для неоднородного участка цепи. Рассмотрим простейшую замкнутую цепь, содержащую источник тока и нагрузку с сопротивлением R (рис. 3.3). Сопротивлением подводящих проводов пренебрегаем. Положив
Идеальный вольтметр, подключенный к зажимам работающего источника тока, показывает напряжение
Отсюда видно, что напряжение U на зажимах работающего источника всегда меньше его ЭДС. Оно тем ближе к Закон Ома позволяет рассчитать любую сложную цепь. Разветвленная цепь характеризуется силой токов, идущих по ее участкам, сопротивлениями участков и ЭДС, включенными в эти участки. Сила тока и ЭДС являются величинами алгебраическими, то есть считаются положительными, если электродвижущая сила способствует движению положительных зарядов в выбранном направлении, а ток течет в этом направлении, и отрицательными в противоположном случае. Однако непосредственный расчет разветвленных цепей бывает сложным. Этот расчет значительно упрощается при использовании правил, предложенных Кирхгофом. Правила Кирхгофа Г. Кирхгоф (1824–1887) детально исследовал закон Ома и разработал общий метод расчета постоянных токов в электрических цепях, в том числе содержащих несколько источников ЭДС. Этот метод основан на двух правилах, называемых законами Кирхгофа. Первое правило Кирхгофа относится к узлам, то есть точкам, в которых сходится не менее трех проводников. Так как мы рассматриваем случай постоянных токов, то в любой точке цепи, в том числе в любом узле, имеющийся заряд должен оставаться постоянным, поэтому сумма притекающих к узлу токов должна быть равна сумме вытекающих. Если условиться считать подходящие к узлу токи положительными, а исходящие – отрицательными, то можно сказать, что алгебраическая сумма сил токов в узле равна нулю:
где n – число проводов, сходящихся в узле.
Второе правило Кирхгофа относится к произвольным замкнутым контурам, которые можно выделить в данной разветвленной цепи. Рассмотрим произвольно замкнутый контур АВСА (рис. 3.4). Направление токов неразветвленных участков можно задать произвольным. Запишем закон Ома для каждого из неразветвленных участков контура АВ, ВС и СА. Обозначим потенциалы узлов через
Сложим почленно все три уравнения, получим:
Можно получить это же соотношение, если условиться, обходя контур в определенном направлении, например, по часовой стрелке, считать положительными те токи, направление которых совпадает с направлением обхода и отрицательными – те, направление которых противоположно направлению обхода. Так же положительными будем считать те ЭДС, которые повышают потенциал в направлении обхода контура и отрицательными – те, которые понижают потенциал в направлении обхода. Эти рассуждения могут быть применены к любому замкнутому контуру, поэтому второе правило Кирхгофа в общем виде можно записать следующим образом:
где n – число участков в контуре, а m – число источников ЭДС. Во втором правиле Кирхгофа находит выражение то очевидное обстоятельство, что при полном обходе контура мы возвращаемся в исходную точку с тем же самым потенциалом. Таким образом, в любом замкнутом контуре, произвольно выбранном в разветвленной цепи проводников, алгебраическая сумма произведений сил токов, текущих через сопротивления соответствующих участков цепи, равна алгебраической сумме ЭДС, встречающихся в этом контуре. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 через поверхность переносится заряд Dq, то сила тока равна:
через поверхность переносится заряд Dq, то сила тока равна: .
. .Ток, не изменяющийся со временем, называется постоянным.
.Ток, не изменяющийся со временем, называется постоянным.
 . Построим на ней бесконечно короткий прямой цилиндр с высотой
. Построим на ней бесконечно короткий прямой цилиндр с высотой  , как указано на рис. 3.1. Все частицы, заключенные внутри этого цилиндра, за время
, как указано на рис. 3.1. Все частицы, заключенные внутри этого цилиндра, за время  пройдут через площадку
пройдут через площадку  , перенеся через нее в направлении скорости
, перенеся через нее в направлении скорости  .
. . Введем вектор
. Введем вектор  , совпадающий по направлению с вектором скорости
, совпадающий по направлению с вектором скорости  и будет плотностью электрического тока. Так как
и будет плотностью электрического тока. Так как  есть объёмная плотность заряда, то плотность тока будет равна
есть объёмная плотность заряда, то плотность тока будет равна  . Если носителями тока являются и положительные, и отрицательные заряды, то плотность тока определится формулой:
. Если носителями тока являются и положительные, и отрицательные заряды, то плотность тока определится формулой: ,
, и
и  – объемные плотности положительных и отрицательных зарядов,
– объемные плотности положительных и отрицательных зарядов,  и
и  – скорости их упорядоченного движения.
– скорости их упорядоченного движения. .
. и сопротивлением r, которое называется внутренним сопротивлением источника. В нагрузке тоже могут действовать сторонние силы, однако в простейших случаях их нет, и нагрузка характеризуется только сопротивлением.
и сопротивлением r, которое называется внутренним сопротивлением источника. В нагрузке тоже могут действовать сторонние силы, однако в простейших случаях их нет, и нагрузка характеризуется только сопротивлением. .
. на некотором участке цепи 1-2, будет равна:
на некотором участке цепи 1-2, будет равна: ,
, – разность потенциалов между концами участка 1-2,
– разность потенциалов между концами участка 1-2,  – электродвижущая сила, действующая на этом участке.
– электродвижущая сила, действующая на этом участке. , совершаемой электрическими и сторонними силами при перемещении единичного положительного заряда, называется падением напряжения или просто напряжением
, совершаемой электрическими и сторонними силами при перемещении единичного положительного заряда, называется падением напряжения или просто напряжением  на данном участке цепи. Следовательно,
на данном участке цепи. Следовательно,  .
. , то есть напряжение совпадает с разностью потенциалов на концах участка цепи.
, то есть напряжение совпадает с разностью потенциалов на концах участка цепи. .
.
 течет ток силой в
течет ток силой в  . Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника
. Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника ,
,
 – длина проводника,
– длина проводника,  – площадь поперечного сечения,
– площадь поперечного сечения,  – зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением. Удельное сопротивление численно равно сопротивлению единицы длины проводника, имеющего площадь поперечного сечения, равную единице.
– зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением. Удельное сопротивление численно равно сопротивлению единицы длины проводника, имеющего площадь поперечного сечения, равную единице. Рис. 3.2
Рис. 3.2
 . Поэтому направления векторов
. Поэтому направления векторов  и
и  . Так как поле внутри выделенного объема можно считать однородным, то напряжение, приложенное к цилиндру, равно
. Так как поле внутри выделенного объема можно считать однородным, то напряжение, приложенное к цилиндру, равно  , где
, где  – напряженность поля в данном месте. Сопротивление цилиндра, согласно (3.2), равно
– напряженность поля в данном месте. Сопротивление цилиндра, согласно (3.2), равно  . Подставив эти значения в формулу (3.1), придем к соотношению:
. Подставив эти значения в формулу (3.1), придем к соотношению: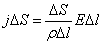 ,
, .
. .
.
 называетсяудельной электрической проводимостью материала. Единицей измерения
называетсяудельной электрической проводимостью материала. Единицей измерения  .
.
 .
. Рис. 3.3
Рис. 3.3
 , получим выражение закона Ома для замкнутой цепи:
, получим выражение закона Ома для замкнутой цепи: .
. , как это следует из закона Ома для однородного участка цепи – в данном случае для сопротивления нагрузки. Подставляя силу тока из этого выражения в закон Ома для замкнутой цепи, получаем:
, как это следует из закона Ома для однородного участка цепи – в данном случае для сопротивления нагрузки. Подставляя силу тока из этого выражения в закон Ома для замкнутой цепи, получаем: .
. напряжение на зажимах разомкнутого источника равно его ЭДС. В противоположном случае, когда R=0, что соответствует короткому замыканию источника тока, U=0, а ток при коротком замыкании максимален:
напряжение на зажимах разомкнутого источника равно его ЭДС. В противоположном случае, когда R=0, что соответствует короткому замыканию источника тока, U=0, а ток при коротком замыкании максимален:  .
. ,
,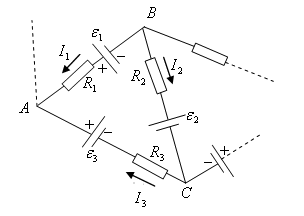 Рис. 3.4
Рис. 3.4
 , тогда:
, тогда: ,
, ,
, .
. .
. ,
,