
|
|
Порядок выполнения работы
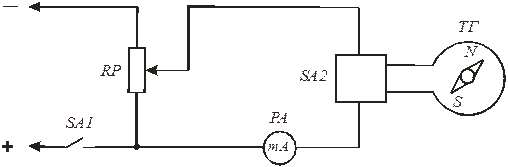
1. Собрать электрическую цепь в соответствии со схемой, представленной на рис.3. Обозначения на рис. 3: SA1, SA2 – переключатели, PA - амперметр, RP- реостат, ТГ- тангенс-гальванометр.
Рис. 3
После проверки электрической цепи преподавателем И разрешения с его стороны
2. Установить плоскость контура тангенс-гальванометра строго в плоскости магнитного меридиана Земли (магнитную стрелку поставить на нуль шкалы компаса). 3. С помощью выключателя SA1 подключить цепь к источнику питания постоянного тока. 4. Потенциометром RP установить заданное преподавателем значение тока I в обмотке тангенс-гальванометра (или значение угла поворота a1 магнитной стрелки компаса). Определить угол поворота a1 магнитной стрелки (или значение силы тока I, если устанавливался угол поворота). Занести измеренные данные в таблицу. 5. Переключателем полярности SA2 изменить направление тока в обмотке тангенс-гальванометра и определить угол поворота a2 магнитной стрелки при том же токе, который занести в таблицу. Изменение направления тока позволяет избавиться от ошибки, создаваемой неточным совпадением плоскости контура тангенс-гальвано-метра с плоскостью магнитного меридиана. 6. Повторить измерения по пп. 2-5 для других значений тока (или углов поворота магнитной стрелки) и записать измеренные значения в таблицу. 7. По формуле (4) рассчитать для каждого тока горизонтальную составляющую напряженности магнитного поля Земли Нt , ее среднее значение < Нt>, погрешности измерения <D Нt>,
Контрольные вопросы 1. Какова основная гипотеза происхождения магнитного поля Земли? 2. Нарисуйте силовые линии геомагнитного поля. Какова напряженность магнитного поля Земли на магнитных полюсах и экваторе? Почему они различны? 3. Сформулируйте и запишите закон Био-Савара-Лапласа в дифференциальной форме. При заданном направлении тока в проводнике определите направление вектора элементарной напряженности магнитного поля в точке наблюдения. 4. Устройство и принцип работы тангенс-гальванометра. 5. Почему при протекании тока в тангенс-гальванометре магнитная стрелка отклоняется от магнитного меридиана? Почему изменение направления тока в обмотке тангенс-гальванометра изменяет положение магнитной стрелки? 6. Почему следует ориентировать плоскость контура тангенс-гальванометра в направлении магнитного меридиана? 7. Почему измерения лучше производить при угле отклонения стрелки тангенс-гальванометра a ~ 45°? 8. Каким образом можно установить наличие магнитного поля?
Рекомендуемая литература 1. Трофимова Т.И. Курс физики. М.: Высшая школа, 1994. § 109, 110. 2. Савельев И.В. Курс общей физики. М: Наука, 1978. Т. 2. § 40, 42, 47. 3. Грабовский Р.И. Курс физики. С-Пб.: Лань, 2002. Часть П, § 24, 26, 27. ЛАБОРАТОРНАЯ РАБОТА № 3-07
Определение коэффициента мощности Электрической нагрузки переменного тока Цель работы: изучить понятие о коэффициенте мощности, определить коэффициент мощности различных электрических нагрузок. Приборы и принадлежности: счетчик электрической энергии, амперметр, вольтметр, комплект ламп накаливания и люминесцентных ламп, электрический секундомер, соединительные провода.
Теория работы
Потребители переменного тока (электрические нагрузки) делят на два вида: активные и реактивные. Реактивные, в свою очередь, бывают емкостными и индуктивными. В активных нагрузках электрическая энергия преобразуется в тепловую (если нагрузка неподвижна и в ней не происходит химических реакций), в механическую работу (если нагрузка движется) или в энергию химических реакций (если они возможны). В реактивных нагрузках энергия накапливается в электрическом поле (в емкости) и магнитном поле (в индуктивности) и не совершает работы. К активным потребителям переменного тока, как правило, относятся нагреватели, лампы накаливания, к активно-индуктивным потребителям – электродвигатели, трансформаторы и электромагниты, а к емкостным – конденсаторы. В активных потребителях (нагрузках) происходит преобразование электрической энергии в тепловую. Количество выделенной теплоты Q при протекании тока I через активную нагрузку R за время t описывается законом Джоуля-Ленца: Q=I2Rt. Величина активного сопротивления зависит от свойств материала проводника (его удельного сопротивления ρ), длины l и сечения S: Всякую активно-индуктивную нагрузку переменного тока можно представить как совокупность двух потребителей: чисто активного R и чисто индуктивного ХL (или идеальной индуктивности). Если катушка индуктивности не содержит активного сопротивления R, то ее называют идеальной; примером служит катушка индуктивности, выполненная из проводника в сверхпроводящем состоянии.
тивление; w -круговая частота; f - частота переменного тока; L - индуктивность катушки. Векторные диаграммы для различных нагрузок представлены на рис. 2. Под векторной диаграммой понимается диаграмма, изображающая совокупность векторов, построенная с соблюдением их взаимной ориентации по фазе. Длина каждого вектора равна амплитуде колебания, а направление вектора образует с некоторой осью (в нашем случае это горизонтальная ось – ось токов Im) угол, равный начальной фазе колебания. Переменное синусоидальное напряжение u=Um sin wt вызывает в активном сопротивлении R протекание тока i=Im sin wt, имеющего такую же начальную фазуj =0, что и вызвавшее его напряжение, или, как говорят, сдвиг фаз j между током и напряжением равен нулю (рис. 2 а). Величины u, i являютсямгновенными значениями напряжения и тока соответственно, а Um , Im – их максимальные (амплитудные) значения. На векторной диаграмме рис. 2 а амплитуды Um , Im направлены вдоль одной прямой.
а) активная б) индуктивная в) активно-индуктивная г) емкостная
Рис. 2
В цепи с чисто индуктивным сопротивлением XL (идеальная катушка индуктивности) напряжение u=Umsin wt будет опережать ток i=Imsin (wt - 900) на угол j = 900 (рис. 2 б), т.е. амплитуды Um и Im на векторной диаграмме взаимно перпендикулярны. В цепи с реальной катушкой индуктивности (активно-индуктивное сопротивление Z) ток i=Im sin (wt -j ) отстает от вызвавшего его напряжения u=Um sin wt на фазу 0<j <900 (рис. 2 в). При включении в цепь переменного тока емкостной нагрузки (конденсатора) напряжение u =Um sin wt вызывает ток i=Im sin (wt+900), т.е. начальная фаза емкостного тока такова, что ток опережает вызвавшее его напряжение на угол j = 900 (рис. 2 г). При этом емкостное сопротивление В цепи переменного тока, содержащей последовательно соединенные нагрузки R, L и C и представляющей собой электрический колебательный контур,при напряжении u =Um sin wt возникает переменный ток i=Im sin (wt±φ). Сдвиг фаз между током и напряжением 0<j <900; знак сдвига фаз φ будет «+», т.е. ток в цепи опережает напряжение, если XL > ХС, и «-», т.е. напряжение опережает ток, если XL< ХС . Учитывая, что при последовательном соединении
UR +UC +UL = Um cos wt, и в векторной диаграмме UC и UL направлены в противоположные стороны вдоль вертикальной прямой (UL опережаетток на
Графической интерпретацией сопротивлений такой цепи является треугольник сопротивлений, катеты которого пропорциональны соответственно активному R и реактивному Х = XL – ХС сопротивлениям, а гипотенуза пропорциональна полному сопротивлению Z (рис. 3 а).
а) б) Рис. 3
Угол j между катетом R и гипотенузой Z треугольника равен углу сдвига фаз j между напряжением и током в данной цепи. Увеличив все стороны треугольника сопротивлений в I2 раз (
Коэффициентом мощности называется величина которая показывает, какую долю составляет активная мощность Р во всей потребленной от источника электрической мощности S. Работа электрического тока равна
А=UIt cosj=U(Icosj)t= UIа t=Рt, (2)
т.е. производится активной составляющей тока Iа=I cosj или активной мощностью Р=UIа= UI cos j. (3)
Реактивная составляющая тока Iр= I sinj работы не производит, она лишь загружает генератор переменного тока и линию. Реактивная мощность, представляющая собой энергию в единицу времени, накапливающуюся в электрическом поле конденсатора и магнитном поле катушки, колеблется между источником электрического тока (генератором) и внешней цепью (за период дважды отдается генератором и дважды возвращается к нему), увеличивая потребляемую от цепи полную мощность. При чисто реактивной нагрузке j = ±900, cos j = 0и выделяемая в цепи активная мощность равна нулю, как бы ни были велики ток и напряжение. Когда включенные в цепь потребители имеют большое реактивное сопротивление (например, электродвигатели, обладающие большой индуктивностью), то cos j < 1. В этих случаях для передачи нужной мощности (при данном напряжении генератора) необходимо увеличивать силу тока, что либо приводит к возрастанию бесполезного тепла Джоуля - Ленца, либо требует увеличения сечения подводящих проводов, возрастания их массы и стоимости. Поэтому на практике стремятся всегда распределить нагрузки таким образом, чтобы cos j был как можно ближе к единице. В Российской Федерации разрешается эксплуатация потребителей переменного тока, коэффициент мощности которых составляет 0,92-0,95. Если cosj потребителей оказывается ниже регламентируемых значений, необходимо применять компенсацию реактивной мощности. В случае активно-индуктивного характера потребителей (что имеет место в большинстве случаев) компенсацию реактивной мощности (сдвига фаз) проводят следующими способами: 1) полная загрузка потребителей (т.е. работа их в режиме расчетной мощности), что не всегда возможно; 2) создание условий, близких к резонансу токов (например, когда большой сдвиг фаз вызван индуктивностью, параллельно нагрузке включают емкость, подобранную так, чтобы 3) получение на месте реактивной составляющей тока, для чего параллельно нагрузке включается генератор переменного тока, называемый синхронным компенсатором, вырабатывающий ток, сдвинутый по фазе на нужный угол j относительно тока, поступающего к потребителю от генератора. Применяется при очень больших потребляемых мощностях. В лабораторной работе в качестве активных потребителей используются лампы накаливания, а в качестве реактивных – люминесцентные лампы. Люминесцентные лампы представляют собой источники света на основе электрического разряда низкого давления, в которых ультрафиолетовое (УФ) излучение ртутного разряда преобразуется люминофором, покрывающим трубку лампы изнутри, в более длинноволновое - видимое излучение. При многих достоинствах – высокой световой отдаче, большом сроке службы, благоприятном спектре излучения, обеспечивающим высокое качество цветопередачи, низкой яркости и низкой температуре поверхности трубки люминесцентные лампы имеют некоторую сложность включения в сеть, связанную с особенностями зажигания разряда. Схема зажигания, называемая пускорегулирующим устройством, содержит индуктивные (дроссель) или емкостно-индуктивные (дроссель-конденсатор) элементы. Дроссель – проволочная катушка с небольшим активным сопротивлением и малыми потерями энергии на нагревание играет роль балластного сопротивления, ограничивающего ток в лампе и обеспечивающего устойчивое горение электрического разряда. Компенсация реактивной мощности люминесцентной лампы с пускорегулирующим устройством, имеющим индуктивный характер (дроссель), достигается подключением параллельно сетевым выводам компенсирующего конденсатора для каждой системы лампа-дроссель (рис. 4) или общего для их группы. На рис. 4 EL - люминесцентная лампа, L– дроссель, С – компенсирующий конденсатор. Тем не менее, коэффициент мощности в скомпенсированной люминесцентной лампе с пускорегулирующим устройством принципиально всегда меньше единицы из-за
ют с помощью счетчиков активной электрической энергии. Важным параметром счетчика электрической энергии является номинальная постоянная счетчика Сн, которая показывает количество энергии, прошедшей через счетчик за время одного оборота его диска. Постоянную Сн для каждого конкретного счетчика можно определить, посмотрев на лицевой панели счетчика число оборотов диска, которое соответствует энергии в 1 кВт× ч = 36× 105 Дж. Величину коэффициента мощности нагрузки можно найти по формуле
где N – число оборотов диска счетчика за время t. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
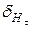 . Таблица
. Таблица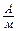
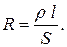
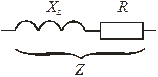 Рис. 1
Рис. 1
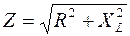 , где XL = wL=2p f L - индуктивное сопро-
, где XL = wL=2p f L - индуктивное сопро-

 , где С - емкость конденсатора.
, где С - емкость конденсатора. , а UC отстает от тока на
, а UC отстает от тока на  где выражение в знаменателе
где выражение в знаменателе 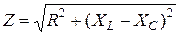 называется полным электрическим сопротивлением цепи переменного тока или импедансом.
называется полным электрическим сопротивлением цепи переменного тока или импедансом. 
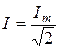 и
и 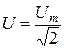 - действующее значение тока и напряжения соответственно), получим треугольник мощностей (рис. 3 б), в котором S=UI – полная мощность, I2R = Р = S соsj –активная мощность, I2(XL –ХС ) = QL - QС = Q = S sinj – реактивная мощность. Из треугольника мощностей для полной мощности получаем
- действующее значение тока и напряжения соответственно), получим треугольник мощностей (рис. 3 б), в котором S=UI – полная мощность, I2R = Р = S соsj –активная мощность, I2(XL –ХС ) = QL - QС = Q = S sinj – реактивная мощность. Из треугольника мощностей для полной мощности получаем 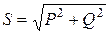 .
.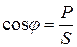 , (1)
, (1)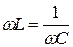 ), что чаще всего и применяется на производстве.
), что чаще всего и применяется на производстве.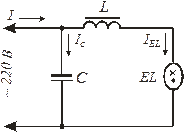 Рис. 4
Рис. 4
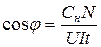 , (4)
, (4)