
|
|
Порядок выполнения работы
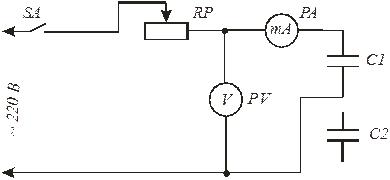
I. Собрать электрическую цепь в соответствии со схемой, представленной на рис. 3, подключив конденсатор С1. Обозначения на рис. 3: SА - выключатель, RР - потенциометр, PA - амперметр, PV- вольтметр, C1, C2 - конденсаторы.
После проверки электрической цепи преподавателем И разрешения с его стороны 2. Включить цепь с конденсатором С1. Определить показания амперметра РА и вольтметра РV при различных положениях движка реостата RР, занести их в таблицу. 3. Отключить конденсатор С1 и подключить конденсатор С2, повторить измерения по п. 2 для него, записать их в таблицу.
Рис. 3
4. Соединить конденсаторы С1 и С2 последовательно и вновь произвести измерения величин тока и напряжения при различных положениях движка реостата RР. 5. Соединить конденсаторы С1 и С2 параллельно и также при различных положениях движка реостата RР произвести измерения величин I и U, занести их в таблицу. Во всех случаях измерений по пп. 2-5 количество измерений должно быть не менее пяти. 6. Занести в таблицу данные вычислений. Найти среднее значение емкости <C>, абсолютную <DС> и относительную dс погрешность ее измерения для каждого из четырех случаев емкости цепи. Результат записать в виде С = <С> ± <DС>. 7. Проверить выполнение законов сложения емкостей для батареи последовательно и параллельно соединенных конденсаторов по формулам (3) и (4) соответственно. Таблица
Контрольные вопросы
1. Что такое конденсатор? Как он изображается в электрических схемах? Где применяется? 2. Что такое емкость конденсатора? В каких единицах измеряется емкость в системе СИ? 3. Емкость плоского конденсатора. 4. Емкость батареи последовательно и параллельно соединенных конденсаторов. 5. Почему постоянный ток не течет через конденсатор, а переменный – течет? 6. Какой физический смысл имеет реактивное сопротивление? 7. Нарисуйте и объясните волновую диаграмму для цепи переменного синусоидального тока с конденсатором. 8. Что такое векторная диаграмма? Постройте векторную диаграмму для цепи переменного синусоидального тока с конденсатором.
Рекомендуемая литература 1. Трофимова Т.И. Курс физики. М.: Высшая школа, 1994. § 93 - 95. 2. Савельев И.В. Курс общей физики. М: Наука, 1978. Т. 2. § 26, 27, 29, 30. 3. Грабовский Р.И. Курс физики. С-Пб.: Лань, 2002. Часть П, § 7, 10, 37.
ЛАБОРАТОРНАЯ РАБОТА № 3-02
Определение коэффициента самоиндукции Катушки индуктивности Цель работы: изучить явление самоиндукции и параметры катушки индуктивности. Определить полное, активное и индуктивное сопротивления катушки И ее индуктивность. Приборы и принадлежности: катушка индуктивности, амперметр, вольтметр, регу- лируемый источник питания постоянного и переменного тока, соеди- нительные провода. Теория работы Катушка индуктивности представляет собой катушку из провода с изолированными витками в виде спирали с сердечником или без него. Если через катушку проходит ток I,то вокруг катушки создается магнитное поле, магнитный поток Ф которого прямо пропорционален току I в катушке:
Ф=LI. (1) Коэффициент пропорциональности L называется коэффициентом самоиндукции или индуктивностью катушки. Индуктивность L катушки зависит от формы, размеров катушки, числа витков, а также от магнитных свойств сердечника. Для жесткой катушки с ферромагнитным сердечником индуктивность L является величиной постоянной, не зависящей от силы тока I. Если ток, проходящий по катушке за время dt, изменится на величину dI, то и магнитный поток, связанный с контуром, изменится на величину
dФ=LdI. (2) В результате этого в катушке (на основании закона электромагнитной индукции) появится электродвижущая сила (ЭДС) самоиндукции
ЭДС самоиндукции зависит от скорости В соответствии с (3) индуктивностью катушки L называется величина, характеризующая связь между скоростью изменения тока в цепи и возникающей при этом ЭДС самоиндукции. Индуктивность катушки сильно увеличивается при внесении внутрь нее сердечника из ферромагнитного материала. Если катушка включена в цепь переменного тока, то в катушке непрерывно возникает ЭДС самоиндукции, для компенсации которой затрачивается часть напряжения источника. Для правильного расчета электрической цепи с катушкой необходимо знать значение ЭДС самоиндукции, а, следовательно, и индуктивность L катушки. Единицу измерения индуктивности катушки легко определить из формулы (3), полагая в ней dt =1 с, dI = 1 А и es = 1 В, тогда единица индуктивности Генри есть индуктивность катушки, в которой изменение тока на 1 А в секунду возбуждает ЭДС самоиндукции, равную 1 В. Одним из способов определения индуктивности L катушки является метод, использующий свойствo катушки индуктивности оказывать реактивное (индуктивное) сопротивление переменному току. Т.к. сила переменного тока в проводнике существенно зависит от формы проводника, то помимо омического сопротивления, которое проводник имеет в цепи постоянного тока, при переменном токе появляется дополнительное сопротивление, зависящее от индуктивности проводника и называемое индуктивным сопротивлением. Индуктивное сопротивление отражает появление ЭДС индукции, т.е. появление дополнительного источника, за счет появления магнитного поля, возбуждающего ЭДС самоиндукции. При включении катушки индуктивности в цепь постоянного тока она имеет активное сопротивление R, которое можно определить по закону Ома:
где U – напряжение на катушке; I - ток, проходящий через катушку. При включении катушки индуктивности в цепь переменного тока ее сопротивление увеличивается и складывается из активного сопротивления R, которое катушка имеет в цепи постоянного тока, определяемого по формуле (4), и индуктивного сопротивления ХL. Полное сопротивление Z катушки индуктивности можно определить из закона Ома
где
Индуктивное сопротивление ХL - это реактивное сопротивление, т.е. сопротивление переменному току, не потребляющее энергии этого тока. Действительно, при протекании переменного синусоидального тока в цепи, обладающей только индуктивным сопротивлением ХL, работа электродвижущей силы (ЭДС) источника в течение одной четверти периода затрачивается на создание тока в катушке. Работа эта превращается в энергию магнитного поля катушки и равна
В течение следующей четверти периода, когда ток в катушке уменьшается, накопленная энергия полностью возвращается к источнику ЭДС. Если через идеальную катушку с индуктивностью L (без активного сопротивления R) идет переменный синусоидальный ток с круговой частотой w
i=Im sin wt, (7)
то в ней возникает электродвижущая сила самоиндукции
где амплитуда
Индуктивное сопротивление XL определяется по формуле
XL = wL=2p f L, (10)
где w =2p f - круговая частота; f - частота. Для реальной катушки индуктивности, которая кроме индуктивности L обладает и активным сопротивлением R, напряжение
uL=Um sin (wt +j), (11)
где j - начальная фаза напряжения. Начальная фаза j определяет сдвиг фаз между напряжением и током на реальной катушке индуктивности, причем напряжение опережает ток на угол j. На рис. 2 а представлена волновая, а на рис. 2 б – векторная диаграмма для реальной катушки индуктивности, иллюстрирующие опережение по фазе напряжением тока через катушку индуктивности. Под векторной диаграммой понимается диаграмма, изображающая совокупность векторов, построенная с соблюдением их взаимной ориентации по фазе. Длина каждого вектора равна амплитуде колебания, а направление вектора образует с некоторой осью (в нашем случае это горизонтальная ось – ось токов Im) угол, равный начальной фазе колебания. UmR , UmL - амплитудные значения напряжения на активной R и индуктивной ХL части катушки индуктивности соответственно.
Рис. 2
Угол между катетом и гипотенузой треугольника сопротивлений (рис. 3) равен углу сдвига фаз j между напряжением и током для данной катушки индуктивности и равен
Для реальной катушки индуктивности сдвиг фаз может изменяться от 0 до 900. Для идеальной катушки индуктивности, в которой R = 0, сдвиг фаз j = 900. Идеальной катушкой индуктивности является катушка, обмотка которой находится в сверхпроводящем состоянии (при температурах ниже критической для данного проводника). В формулы (7) - (9), (11) входят амплитуды Um и Im, не измеряемые приборами. Показания приборов в цепях переменного синусоидального тока соответствуют действующим значениям напряжения
Определив активное сопротивление R катушки по формуле (4) и полное сопротивление Z по формуле (5), найдем индуктивное сопротивление ХL из формулы (12):
В Российской Федерации стандартная частота переменного синусоидального тока равна f = 50 Гц. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
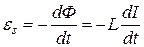 . (3)
. (3) изменения тока и от индуктивности L катушки. Знак «-» показывает, что ЭДС самоиндукции всегда направлена против причины, которая ее вызывает (т.е. против напряжения, приложенного к катушке) – это правило Ленца.
изменения тока и от индуктивности L катушки. Знак «-» показывает, что ЭДС самоиндукции всегда направлена против причины, которая ее вызывает (т.е. против напряжения, приложенного к катушке) – это правило Ленца. Гн - эта единица называется генри (Гн).
Гн - эта единица называется генри (Гн).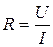 , (4)
, (4)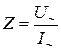 , (5)
, (5)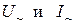 - переменное напряжение и ток соответственно.
- переменное напряжение и ток соответственно. Рис. 1
Рис. 1
 . (6)
. (6)
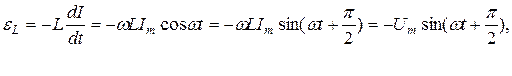 (8)
(8)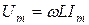 ; Um и Im - максимальное (амплитудное) значение напряжения и тока соответственно. Тогда напряжение на катушке индуктивности
; Um и Im - максимальное (амплитудное) значение напряжения и тока соответственно. Тогда напряжение на катушке индуктивности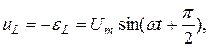 (9) что означает, что напряжение на индуктивности опережает ток на угол
(9) что означает, что напряжение на индуктивности опережает ток на угол 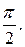
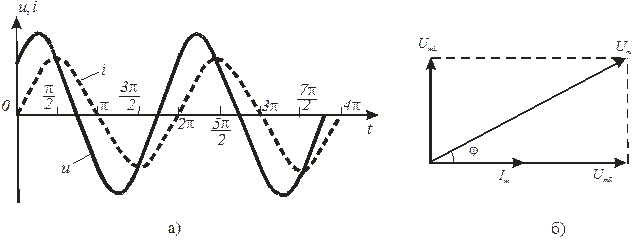
 Рис. 3
Рис. 3
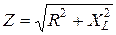 . (12)
. (12)
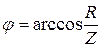 . (13)
. (13) и тока
и тока 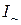 , которые связаны с амплитудами Im и Um посредством формул
, которые связаны с амплитудами Im и Um посредством формул . (14)
. (14)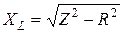 , откуда с учетом (10) получим индуктивность катушки:
, откуда с учетом (10) получим индуктивность катушки: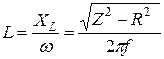 . (15)
. (15)