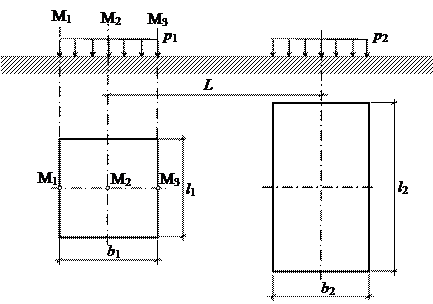
|
|
В массиве грунта от совместного действия равномерноРаспределенных по прямоугольным площадям нагрузок Построить эпюры вертикальных сжимающих напряжений в массиве грунта от совместного действия равномерно распределенных по прямоугольным площадям нагрузок p1 и p2 (рис. 3.1) в точках на заданной вертикали. Исходные данные – по табл. 3.1.
Рис. 3.1. Схема к задаче 3 Таблица 3.1. Исходные данные к задаче 3
Пример Построить эпюры вертикальных сжимающих напряжений от совместного действия равномерно распределенных по прямоугольным площадям нагрузок p1=310 кПа и p2= 410 кПа (рис. 3.2) в точках на вертикали M2. Размеры площадей: l1=2,5 м, b1=2,5 м; l2=4,0 м, b2=2,4 м. Расстояние между осями фундаментов L=3,4 м. Расчетная вертикаль М2.
Рис. 3.2. Схема расположения площадей нагрузки Решение Напряжение, возникающее в грунте под центром прямоугольной площади загружения равномерно распределенной нагрузкой, находят по формуле
где a - коэффициент, определяемый по СНиП [2] в зависимости от соотношений Напряжения в угловых точках прямоугольной площади загружения определяются по формуле
где a принимается также по СНиП [2], но для Для расчета напряжений в массиве грунта с учетом влияния соседних площадей загружения будем использовать метод угловых точек, в соответствии с которым вертикальные нормальные напряжения на глубине z по вертикали М2
где Выполним построение, приложив фиктивную нагрузку по прямоугольнику АВEG, имеющую то же значение, что и заданная p2, но действующую в другом направлении (рис. 3.3). Разобьем прямоугольник ABCD на четыре прямоугольника M2BCN, AM2ND, M2BEK, AM2KG, для которых точка M2 является угловой.
Рис. 3.3. Схема расположения действительной и фиктивной нагрузок
Определяем значения h для рассматриваемых площадей загружения: для рассчитываемой площади загружения
для прямоугольников M2BCN и AM2ND
для прямоугольников M2BEK и AM2KG
Разбиваем массив грунта на слои толщиной
Вычисляем напряжения на границах слоев, результаты вычисления сводим в таблицу.
Таблица 3.2. Величины вертикальных сжимающих напряжений в массиве грунта
Примечание. Напряжения от рассчитываемой площади загружения определяются по формуле
Рис. 3.4. Эпюра вертикальных сжимающих напряжений
Эпюра вертикальных сжимающих напряжений в массиве грунта в точках на вертикали М2 показана на рис. 3.4.
Задание 4. Определение вертикальных сжимающих напряжений В массиве грунта от действия полосовой нагрузки Построить эпюры вертикальных сжимающих напряжений в массиве грунта от действия полосовой нагрузки р, изменяющейся по закону прямой в точках на заданной вертикали и горизонтали, расположенной на расстоянии z от поверхности (рис. 4.1). Точки по вертикали на глубине 0, 1, 2, 4 и 6 м, по горизонтали на границах и в середине треугольной и равномерно распределенной нагрузок. Исходные данные – по табл. 4.1.
Рис. 4.1. Схема к задаче 4
Таблица 4.1. Исходные данные к задаче 4
Пример Построить эпюры вертикальных сжимающих напряжений в массиве грунта от действия полосовой нагрузки p =200 кПа, изменяющейся по закону прямой в точках на заданной вертикали и горизонтали, расположенной на расстоянии z =2 м от поверхности (рис. 4.2). Ширина треугольной нагрузки b1 = 2 м, ширина прямоугольной нагрузки b2 = 2 м. Точки по вертикали M3 на глубине 0, 1, 2, 4 и 6 м, по горизонтали на границах и в середине треугольной и прямоугольной нагрузок.
Рис. 4.2. Схема расположения нагрузок и точек определения вертикальных сжимающих напряжений
Решение Примем координатную систему yz. Для распределенной полосовой нагрузки шириной b, изменяющейся по закону треугольника, вертикальные напряжения в грунтовом массиве определяются по формуле
где Kz – коэффициент, зависящий от соотношений z/b и y/b и определяемый по [4], y – горизонтальная координата рассматриваемой точки от оси, проходящей через вершину треугольной нагрузки; z – вертикальная координата точки от ограничивающей плоскости. Для равномерно распределенной полосовой нагрузки шириной b вертикальные напряжения в грунтовом массиве определяются по той же формуле, что и для треугольной, но горизонтальная координата y отсчитывается от оси симметрии прямоугольной нагрузки. Вертикальные сжимающие напряжения от совместного действия треугольной и прямоугольной нагрузок определяются суммированием напряжений от соответствующих нагрузок. Определим напряжения по вертикали М3. Для точки, находящейся на глубине z1=0, отношения Напряжение от совместного действия треугольной и прямоугольной нагрузок
Для точки, находящейся на глубине z2=1 м, отношения Напряжение
Для точки, находящейся на глубине z3=2 м, отношения Напряжение
Для точки, находящейся на глубине z4=4 м, отношения Напряжение
Для точки, находящейся на глубине z5=6 м, отношения Напряжение
Определим напряжения на горизонтальной прямой в точках A, В, С, D на глубине z =2 м. Для точки А отношения Напряжение
Для точки B отношения Напряжение
Для точки C отношения
Напряжение
Для точки D отношения Напряжение
Для точки E напряжения
Рис. 4.3. Эпюры вертикальных сжимающих напряжений Задание 5. Определение устойчивости откоса методом 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
,
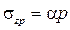и 
. Здесь b и l – соответственно ширина и длина прямоугольника; p – равномерно распределенное давление.
,
.
определяются алгебраическим суммированием напряжений от рассчитываемой и соседних площадей загружения по формуле
,
– вертикальное напряжение на глубине z от рассчитываемой площади загрузки; k – число соседних площадей загрузки;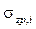 
– давление, передаваемое соседней i-ой площадью загружения.
,
,
.
.
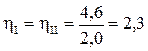кПа, от дополнительных площадей загружения I и II –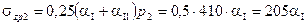 
кПа, от фиктивных площадей загружения III и IV - 
.
,
; 
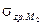
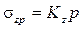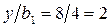для треугольной нагрузки; 
; 
для прямоугольной нагрузки. Значения коэффициентов Kz будут следующими: Kz1 = 0; Kz2 = 0,5.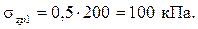
; 
. Значения коэффициентов: Kz1 = 0,003; Kz2 = 0,5.
; 
. Значения коэффициентов: Kz1 = 0,0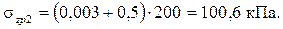17; Kz2 = 0,48.
; 
. Значения коэффициентов: Kz1 = 0,045; Kz2 = 0,41.
; 
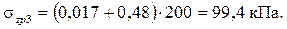
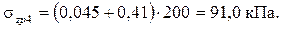
. Значения коэффициентов: Kz1 = 0,062; Kz2 = 0,33.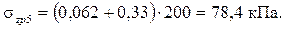
; 
; 
; 
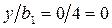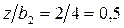. Значения коэффициентов: Kz1 = 0,127;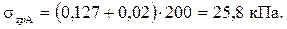
; 
; 
; 
; 
; 
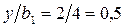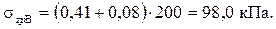
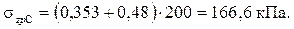
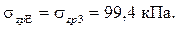
Построим эпюры вертикальных напряжений, откладывая ординаты соответствующих значений в расчетных точках по вертикали и горизонтали ( рис 4.3).