
|
|
Операторные схемы замещения
Рассмотрим составление операторной схемы замещения на примере электрической цепи, приведенной на рис.7.2.
Для их определения составляется система уравнений по законам Кирхгофа, описывающая режим работы цепи, до замыкания ключа.
Рассмотрим систему уравнений (7.3) с точки зрения установившегося режима, так как до начала переходного процесса в цепи наблюдается установившийся режим. При действии постоянного напряжения производные от токов и напряжений цепи будут равны нулю. С учетом последнего замечания система уравнений (7.3) принимает вид:
В системе уравнений (7.4) ток конденсатора принимается равным нулю, так как
Определим из системы уравнений (7.4) значение тока индуктивности и напряжения на конденсаторе.
Используя таблицу 7.1 и схемы замещения, приведенные на рис.7.1, составим операторную схему замещения электрической цепи, приведенной на рис.7.2 с учетом выражений (7.5). Схема оставляется для цепи, полученной после коммутации цепи (рис.7.3).
величиной LiL(-0) и Uc(-0) /p.
Составление операторных решений
Рассмотрим порядок составления операторных решений на примере электрической цепи, приведенной на рис. 7.4.
После выбора рационального метода расчета определяются операторные изображения токов в ветвях и напряжений на элементах цепи. Составим уравнение по методу контурных токов для цепи, приведенной на рис. 7.4. Выберем направления контурных токов и направлений обхода контуров по часовой стрелке.
Найдем операторные выражения для контурных токов. Выразим из первого уравнения системы (7.6) ток
Подставим выражение (7.7) во второе уравнение системы уравнений (7.6) и выразим ток
После несложных преобразований получим операторное изображение тока
Определим операторные изображения для токов ветвей цепи.
Рассмотрим выражения (7.8), (7.9) и (7.10). Знаменатели этих выражений получились одинаковыми или отличаются на множитель p. При нахождении операторных изображений токов в ветвях и напряжений на элементах цепи знаменатели должны получаться одинаковыми или могут отличаться на оператор p.
Определение оригиналов
Если полученное операторное изображение тока и напряжения имеет табличный вид, то нахождение оригинала осуществляется с помощью таблицы 7.1. Если полученная функция не имеет табличного вида, то переход к оригиналу осуществляется при помощи теоремы разложения. В этом случае полученную функцию I(p) или U(p) представляют в виде отношения двух многочленов.
Определяются корни уравнения M(p)=0. В зависимости от вида корней знаменателя теорема разложения может иметь следующие формы: 1. Если корни уравнения M(p)=0 разные и среди них нет корней равным корням уравнения N(p)=0, то оригинал тока i(t), соответствующий изображению (7.11), может быть найден согласно теореме разложения:
где m – число корней знаменателя M(p)=0. 2. Если в уравнении M(p)=0 имеется n различных корней p1, p2,… , pn и из них корень p1 кратностью m1, корень p2 кратностью m2, то оригинал тока будет вычисляться по формуле:
Здесь выражение, стоящее в знаменателе квадратной скобки, надо сначала сократить на (p-pk)mk и лишь после этого дифференцировать. Второй путь предполагает представление операторного изображения I(p) или U(p) в виде простых дробей. Переход к оригиналу для суммы простых дробей может быть осуществлен при помощи таблиц оригиналов и изображений. 3. Если среди n корней имеется пара комплексных сопряженных корней
Найдем оригинал тока iL(t) по его операторному изображению (7.10). Зададимся параметрами цепи: R1=10 Ом, L=0,1 Гн, C=100 мкФ, напряжение источника U=100 В. Принимаем iL(-0) =5 А, Uc(-0) =50 В. Подставим численные данные в выражение (7.10) и преобразуем его, определив коэффициенты многочленов числителя и знаменателя.
Определим корни многочленов числителя и знаменателя.
Сравнивая корни числителя и знаменателя можно сделать вывод, что среди них нет равных корней, поэтому применяется форма теоремы разложения (7.12):
Найдем значения многочлена числителя путем подстановки в N(p) корней знаменателя.
Возьмем производную от многочлена знаменателя .
Найдем значения производной M'(p) для корней знаменателя.
Определим оригинал тока iL(t)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Рисунок 7.2
Рисунок 7.2
 (7.3)
(7.3) (7.4)
(7.4)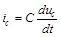 .
.

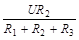 . (7.5)
. (7.5) Рисунок 7.3
Рисунок 7.3

 ,
, . (7.6)
. (7.6) .
. . (7.7)
. (7.7) .
. . (7.8)
. (7.8) . (7.9)
. (7.9)


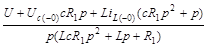 . (7.10)
. (7.10) . (7.11)
. (7.11)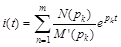 , (7.12)
, (7.12) . (7.13)
. (7.13) ; то теорема разложения может быть представлена в следующем виде:
; то теорема разложения может быть представлена в следующем виде: . (7.14)
. (7.14) . (7.15)
. (7.15)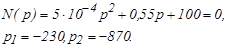 (7.16)
(7.16)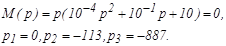 (7.17)
(7.17) .
.
 (7.18)
(7.18)
 .
. ,
,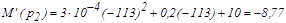 ,
, .
.