
|
|
Таким образом, теоретическая цена акции прямо пропорциональна дивиденду по ней и обратно пропорциональна ставке процента, учитываемого при оценивании.Если все же предположить, что через n лет акция будет продана, то цена акции будет равна сумме приведенных величин потока дивидендов и цены реализации, т.е.:
где Рn — цена реализации акции. Оценка акций, по приведенным формулам, носит весьма условный характер, так как величины, входящие в них — дивиденды и уровень ссудного процента (i) — являются трудно предсказуемыми. Вместе с тем уровень реальных цен складывается под влиянием прогнозных оценок, которые исходят из имеющейся информации о продуктивности каждой корпорации, ее дивидендной политики, а также расчет эффективности альтернативных вложений.
9.5.3 Формирование портфеля акций и оценка его доходности
Формируя инвестиционный портфель (портфель акций), инвесторы пытаются при минимальном риске получить максимальную прибыль. Достижение этой цели возможно только при принятии компромиссного решения, уравновешивающего эти факторы. Создание оптимальной структуры инвестиционного портфеля зависит от знания ситуации на фондовом рынке и возможности ее прогнозирования. Значительную часть процессов, происходящих в рыночной экономике, нельзя с достаточной степенью достоверности оценить заранее. Единственный способ научно-обоснованного прогноза заключается в статистическом анализе экономических процессов. Использование данного метода дает возможность на основе прошлых наблюдений обнаружить тенденции развития изучаемых процессов и выявить количественную взаимосвязь между ними. Основой такого анализа является вероятностно-статистические методы, которые оперируют приближенными вероятностными характеристиками и условными допущениями. Применение этих методов требует использования ряда положений (формул) математической статистики. Предложим ряд формул без их доказательства, т.е. представим их в конечном виде. В основу наших рассуждений положим показатель прибыльности акций на определенный период, рассчитываемый по (1). Одновременно на фондовом рынке объектом купли-продажи являются акции большого числа эмитентов, имеющие разную степень доходности. Среднюю рыночную доходность этих акций (rm) определяют по формуле:
где ri — доходность i акций; N — количество всех акций на рынке; xi — удельный вес i-тых акций, определяемый как отношение объема их выпуска к суммарному объему всех выпусков (в рыночных ценах на соответствующий момент). Расчеты показателя rm производят по акциям наиболее представительных компаний. В США чаще всего используется индекс Standart & Poors, рассчитываемый по акциям 500 крупнейших компаний, или известный индекс Доу-Джонса. В России существует фондовый индекс "АК & М" включающий в себя три показателя: "Индекс акций банков", "Индекс акций промышленных предприятий" и "Сводный индекс". В основу формирования индексов положена методика компании Standart & Poors. Допустим, что рыночные показатели эффективности (доходности) — rm всех акций, обращающихся на фондовом рынке, отобраны за К периодов. За те же периоды отобраны показатели эффективности акций i-того вида — ri,. Таким образом, мы получили два массива данных: (rm1 , rm2 , ... ,rmk) и (ri1 , ri2 , .. ., rik). Используя эти данные, можно рассчитать средние арифметические величины показателей эффективности акций, т.е.
Дадим интерпретацию этим показателям. На протяжении рассматриваемого периода в К лет (месяцев, кварталов) доходность по рынку акций в целом и по отдельным акциям в каждом году (месяце) была близка к показателям Величину фактического отклонения (вариацию) показателей эффективности мы измерили с помощью статистического показателя вариации — среднего квадратичного отклонения (7; 8). В случаях, когда вариация эффективности равна нулю:
показатель эффективности не отклоняется от своего среднего значения, т.е. нет неопределенности, а значит, и риска.Чем больше вариация, тем больше и величина среднего квадратичного отклонения, т.е. выше неопределенность и риск. Поэтому можно считать величину Если эти параметры будут соотноситься как Инвестиции в ценные бумаги всегда сопровождаются необходимостью решения дилеммы:вкладывать деньги в акцию с большим доходом и большим риском, или довольствоваться меньшим доходом, но и меньшим риском. Выбор варианта зависит от характера инвестора, суммы инвестиций и ее доли в общем капитале инвестора.
9.5.4 Основные характеристики облигаций и методы расчета их доходности Облигации относятся к ценным бумагам с фиксированным доходом. Они могут выпускаться государством, региональными властями, финансовыми институтами, а также различными корпорациями. Облигация : * ценная бумага, удостоверяющая отношения займа между кредитором-владельцем облигации и должником-эмитентом облигации; * удостоверяет внесение ее владельцем денежных средств и подтверждает обязательство возместить ему номинальную стоимость облигации в заранее установленный срок с уплатой фиксированного процента. К основным параметрам облигации относятся: * номинальная цена, * выкупная цена в случае, если она отличается от номинальной, * норма доходности и * сроки выплаты процентов. Момент выплаты процентов оговаривается в условиях эмиссии и может производиться раз в год, по полугодиям или поквартально. В мировой практике используется несколько способов выплаты доходов по облигациям, в их числе: установление фиксированного процентного платежа, применение ступенчатой процентной ставки, использование плавающей ставки процентного дохода, индексирование номинальной стоимости облигации, реализация облигаций со скидкой (дисконтом) против их нарицательной цены, проведение выигрышных займов. Установление фиксированного процентного платежа является распространенной и наиболее простой формой выплаты дохода по облигациям. При использовании ступенчатой процентной ставки устанавливается несколько дат, по истечении которых владельцы облигаций могут либо их погасить, либо оставить до наступления следующей даты. В каждый последующий период ставка процентов возрастает. Ставка процента по облигациям может быть плавающей, т.е. изменяющейся регулярно каждые полгода и т.д., в соответствии с динамикой ставки рефинансирования Центрального банка или уровнем доходности государственных ценных бумаг, размещаемых путем аукционной продажи. В отдельных странах в качестве антиинфляционной меры практикуют выпуск облигаций с номиналом, индексируемым с учетом роста индекса потребительских цен. По некоторым облигациям проценты не выплачиваются. Их владельцы получают доход благодаря тому, что покупают эти облигации с дисконтом (скидкой против нарицательной стоимости), а погашают — по номиналу. Доход по облигациям может выплачиваться в форме выигрышей, достающихся отдельным их владельцам по итогам регулярно проводимых тиражей. Облигации, являясь объектом купли-продажи на рынке ценных бумаг, имеют рыночную цену, которая в момент эмиссии может быть равна номиналу, а также быть ниже или выше его. Рыночные цены существенно различаются между собой, поэтому для достижения их сопоставимости рассчитывается курс облигации. Под курсом облигации понимают покупную цену одной облигации в расчете на 100 денежных единиц номинала. Курс облигации зависит от средней величины ссудного процента на рынке капиталов, существующего в данный момент, срока погашения, степени надежности эмитента и ряда других факторов. Расчет курса производится по формуле:
где Рk — курс облигации; Р — рыночная цена; N — номинальная цена облигации. Доходность облигации характеризуется рядом параметров, которые зависят от условий, предложенных эмитентом. Так, например, для облигаций, погашаемых в конце срока, на которые они выпущены, доходность измеряется купонной доходностью, текущей доходность и полной доходностью. 4.1 Купонная доходность — норма процента, которая указана на ценной бумаге и которую эмитент обязуется уплатить по каждому купону. Платежи по купонам могут производиться раз в квартал, по полугодиям или раз в год. Например, на облигации указана купонная доходность в 11,75% годовых. Номинал облигации 100 грн. На каждый год имеется два купона. Это значит, что облигация принесет полугодовую прибыль 5,875 грн. (100 х 0,1175 х 0,50), а за год 11,75 грн.
4.2 Текущая доходность - характеризует выплачиваемый годовой процент на вложенный капитал, т.е. на сумму, уплаченную в момент приобретения облигации. Текущая доходность определяется по формуле:
где g - норма доходности по купонам; N — номинальная цена облигации; Р — рыночная цена (цена приобретения). Например, если купонная доходность g = 11,71%, а курс облигации 95,0, то текущая доходность составит:
Вместе с тем текущая доходность не учитывает изменения цены облигации за время ее хранения, т.е. другого источника дохода. 4.3 Полная доходность учитывает все источники дохода. Показатель полной доходности измеряют процентной ставкой, называемой ставкой помещения. Начисление процентов по ставке помещения на цену приобретения дает доход, эквивалентный фактически получаемому по ней доходу за весь период обращения этой облигации до момента ее погашения. Ставка помещения является расчетной величиной и в явном виде на рынке ценных бумаг не выступает. Стоимость облигации равна сумме двух слагаемых - современной стоимости ее аннуитетов (приведенной сумме ежегодных выплат процентных платежей) и современной стоимости ее номинала:
если использовать (21), то:
где Р — рыночная цена облигации; Рk — курс облигации; N — номинал облигации; g — купонная ставка; n — время от момента приобретения до момента погашения облигации; i — ссудный процент, предлагаемый банками в момент продажи облигации;
Пример По облигации номинальной стоимостью в 100 грн. в течение 10 лет (срок до ее погашения) будут выплачиваться ежегодно в конце года процентные платежи в сумме 10 грн. (g = 10%), которые могут быть помещены в банк под 11% годовых. Рыночная цена облигации по (23) составит:
а рыночный курс:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
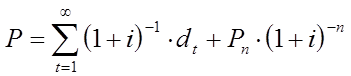 (9.5)
(9.5) (9.6)
(9.6) и
и  , а также среднеквадратические отклонения этих показателей:
, а также среднеквадратические отклонения этих показателей: (9.7)
(9.7) (9.8)
(9.8) ;
; 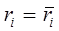 ,
, - мерой риска.Предположим: инвестору предложены два вида ценных бумаг с параметрами:
- мерой риска.Предположим: инвестору предложены два вида ценных бумаг с параметрами:  , а
, а  . Т.е. доходность i-тых бумаг больше, чем .j-тых, а риск меньше. Естественно, грамотный инвестор выберет бумаги с показателем эффективности
. Т.е. доходность i-тых бумаг больше, чем .j-тых, а риск меньше. Естественно, грамотный инвестор выберет бумаги с показателем эффективности  .
. а
а 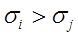 . , то инвестор выберет бумаги с показателем эффективности
. , то инвестор выберет бумаги с показателем эффективности  .
.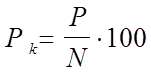 (9.9)
(9.9) (9.10)
(9.10)
 , (9.11)
, (9.11) (9.12)
(9.12) --- коэффициент приведения ренты, (смотрите методические указания по дисциплине «Анализ инвестиционных проектов» практическое занятие 2.1).
--- коэффициент приведения ренты, (смотрите методические указания по дисциплине «Анализ инвестиционных проектов» практическое занятие 2.1). ,
, .
.